
 Глава 1. Задачи для самостоятельного решения |
Глава 1. Задачи для самостоятельного решения | 
| Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
 |
||
 Глава 1. Задачи для самостоятельного решения | Глава 1. Задачи для самостоятельного решения | |
Оглавление | | Глава 2  |
| Решения |
б) Возьмем на стороне AD точку F так, что BF||CD. Пусть
E — точка пересечения отрезков MN и BF. Тогда
| MN = ME + EN = |
qAF
| + b = |
q(a – b) + (p + q)b
| = |
qa + pb
| . |
б) Пусть BA1 : A1C = 1 : p и AB1 : B1C = 1 : q. Тогда
AD : DA1 = (1 + p) : q и BD : DB1 = (1 + q) : p. Поэтому
| a1 = |
1 + p + q
|
| b1 = |
1 + p + q
|
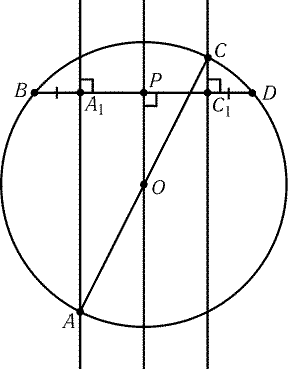
Рис. 1.3
б) Пусть D и E — точки пересечения прямых AB1 и CA1, CB1 и AC1. Тогда CA1 : A1D = CB : BA = EC1 : C1A. А так как DCB1D ~ DEB1A, точки A1, B1 и C1 лежат на одной прямой.
Рис. 1.4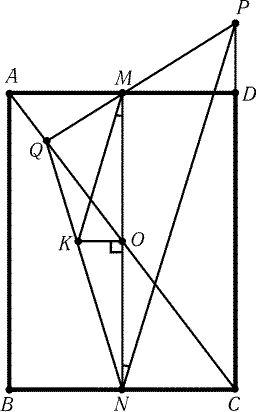
|
® N1N | = b |
® RR1 | = ab |
® DD1 |
|
® N2N | = a |
® SS1 | = ab |
® DD1 | . |
Замечание. В случае a = b есть более простое решение. Так как BP : BA = BQ : BC = a, то PQ||AC и PQ : AC = a. Аналогично RS||AC и RS : AC = 1 – a. Поэтому отрезки PR и QS делятся точкой их пересечения в отношении a : (1 – a).
б) Учитывая, что BA1 : A1C = BA : AC и BA1 + A1C = BC, получаем BA1 = ac/(b + c). Так как BO — биссектриса треугольника ABA1, то AO : OA1 = AB : BA1 = (b + c) : a.
| R = BO = a2/ | Ц |
4a2 – b2
| . |
|
1
| + |
1
| = |
(cos 2j + sin 2j)
| = |
1
| . |
б) Пусть O — центр вписанной окружности. Так как РCBA + РBAD = 180°, то РABO + РBAO = 90°. Поэтому DAKO ~ DOKB, т. е. AK : KO = OK : KB. Следовательно, AK · KB = KO2 = R2, где R — радиус вписанной окружности. Аналогично CL · LD = R2.
|
AB
| + |
AD
| = |
ABў
| + |
ADў
| = |
CDў + ADў
| = |
AC
| . |
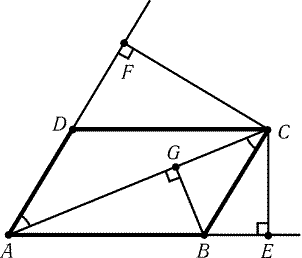 Рис. 1.5 |
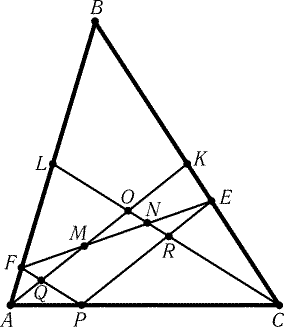 Рис. 1.6 |
Рис. 1.7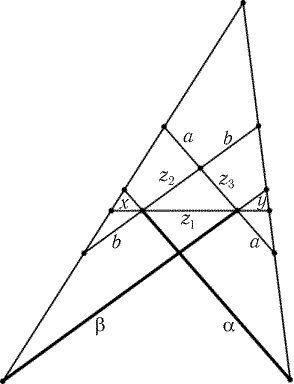
| 1
| + | 1
| = | 1
| . |
|
x
| = |
x + z1
|
|
a + z3
| = |
b
|
|
y + z1
| = |
y
|
|
a
| = |
b + z2
|
Пусть точки B1 и C1 симметричны B и C относительно серединного перпендикуляра к отрезку MN. Так как AM : NB = MN : BM = MC : NC, то MA · MC1 = AM · NC = NB · MC = MB1 · MC. Следовательно, точка A лежит на окружности, описанной вокруг трапеции BB1CC1.
Возможны два варианта: РABE = РCBE или РABE = РBCE. Первый вариант отпадает, так как в этом случае DABE = DCBE. Остается второй вариант. В этом случае РABC = РABE + РCBE = РABE + РBAE = 90°. В прямоугольном треугольнике ABC катеты относятся, как 1 : Ц3, поэтому его углы равны 90°,60°,30°.
| SBDEF/2SADE = SBDE/SADE = DB/AD = EF/AD = | Ц |
SEFC/SADE
|
| SBDEF = 2 | Ц |
SADE · SEFC
|
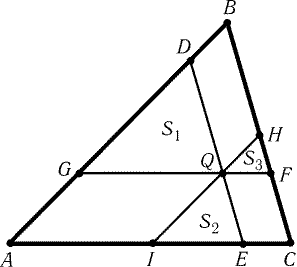
Рис. 1.8
|
| S = ( | Ц |
S1
| + | Ц |
S2
| + | Ц |
S3
| . )2 |
а) Ясно, что
| SAEH + SCFG = |
SABD
| + |
SCBD
| = |
SABCD
|
| SBEF + SDGH = |
SABCD
|
| SEFGH = SABCD – |
SABCD
| – |
SABCD
| = |
SABCD
| . |
б) Так как AC = BD, то EFGH — ромб (задача 1.2). Согласно задаче a) SABCD = 2SEFGH = EG · FH.
Второе решение. Так как DE = 1, EA = Ц2, EB = 2,AD = Ц5 и
| BA = | Ц |
10
|
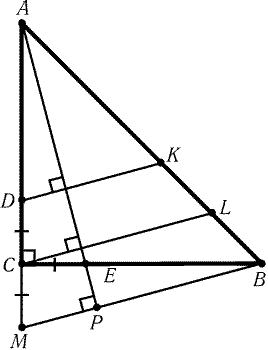 Рис. 1.10 |
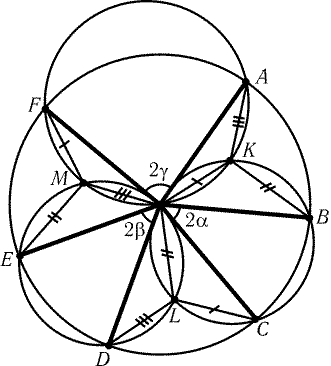 Рис. 1.11 |
Рис. 1.12
б) Возьмем на сторонах AB и AC такие точки Bў и Cў, что ABў : AB = ACў : AC = 2 : 3. Середина M отрезка BўCў совпадает с точкой пересечения медиан треугольника ABC. Построим на сторонах ABў и ACў внешним образом прямоугольные треугольники ABўC1 и AB1Cў с углом j = 60°. Тогда B1 и C1 — центры правильных треугольников, построенных на сторонах AB и AC; с другой стороны, согласно задаче а) MB1 = MC1 и РB1MC1 = 120°.
Замечание. Утверждения задач а) и б) остаются верными и для треугольников, построенных внутренним образом.
б) Построим на стороне BC внешним образом равнобедренный треугольник BA1C с углом 360° – 2j при вершине A1 (если j < 90°, строим внутренним образом треугольник с углом 2j). Так как сумма углов при вершинах трех построенных равнобедренных треугольников равна 360°, треугольник A1B1C1 имеет углы 180° – j,j/2 и j/2 (см. задачу 1.48). В частности, этот треугольник равнобедренный, а значит, A1 = O.
б) Так как OA^l и l||B1C1, то OA^B1C1.
Если AH · A1H = BH · B1H = CH · C1H, то DA1BH ~ DB1AH, а значит, РBA1H = РAB1H = j. Поэтому РCA1H = РCB1H = 180° – j. Аналогично РAC1H = РCA1H = 180° – j и РAC1H = РAB1H = j, поэтому j = 90° т. е. AA1,BB1 и CC1 — высоты.
б) Прямые AB,BC и CA являются биссектрисами внешних углов треугольника A1B1C1, поэтому A1A — биссектриса угла B1A1C1, а значит, AA1^BC. Для прямых BB1 и CC1 доказательство аналогично.
Рис. 1.13
б) Так как углы между диаметром AC и касательными к окружностям в точках F,D,E равны, то РFAB = РDAC = РEBC и РFBA = РDCA = РECB, т. е. F лежит на отрезке AD, E — на отрезке DC. Кроме того, РAFB = РBEC = РADC = 90°, поэтому FDEB — прямоугольник.
Так как TM1 = RM = AQ и TM1||AQ, то AM1||TQ. Аналогично AP1||RP. Поскольку РM1AP1 = 90°, то RP^TQ.
Обозначим точки пересечения прямых TQ и RP, M1A и RP, P1A и TQ через E,F,G соответственно. Чтобы доказать, что точка E лежит на прямой AC, достаточно доказать, что прямоугольники AFEG и AM1CP1 подобны. Так как РARF = РAM1R = РM1TG = РM1CT, можно обозначить величины этих углов одной буквой a. AF = RAsin a = M1Asin 2a, AG = M1Tsin a є M1Csin 2a, поэтому прямоугольники AFEG и AM1CP1 подобны.
|
 Глава 1. Задачи для самостоятельного решения | Глава 1. Задачи для самостоятельного решения | |
Оглавление | | Глава 2  |
 |
| Copyright © 2002 МЦНМО |
Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru. |
|