Согласно задаче 3.2 CM = (AC + CE – AE)/2
и CN = (BC + CE – BE)/2. Учитывая, что AC = BC,
получаем MN = |CM – CN| = |AE – BE|/2.
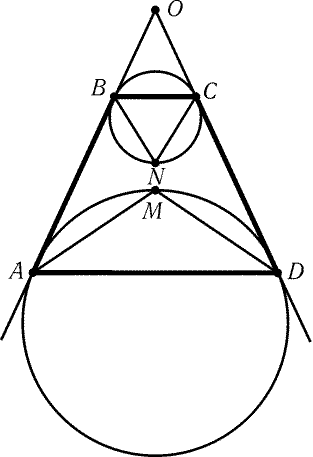
Рис. 3.8
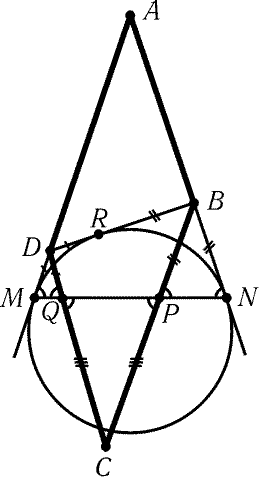
Рис. 3.9
3.4. Пусть прямые AB,BC,CD и DA касаются окружности
в точках P,Q,R и S. Тогда CQ = CR = x, поэтому BP = BC + CQ = BC + x
и DS = DC + CR = DC + x. Следовательно, AP = AB + BP = AB + BC + x
и AS = AD + DS = AD + DC + x. Учитывая, что AP = AS, получаем требуемое.
3.5. Пусть прямая AB касается окружностей с центрами O1
и O2 в точках C и D. Так как РO1AO2 = 90°,
прямоугольные треугольники AO1C и O2AD подобны.
Поэтому O1C : AC = AD : DO2. Кроме того, AD = CB
(см. задачу 3.2). Следовательно, AC · CB = Rr.
3.6. Пусть прямые AB и CD пересекаются в точке O. Для
определенности будем считать, что точки A и D принадлежат
первой окружности, а B и C- второй, причем OB < OA (рис. 3.8).
Точка M пересечения биссектрис углов A и D четырехугольника ABCD
является серединой той дуги первой окружности, которая
лежит внутри треугольника AOD, а точка N пересечения биссектрис
углов B и C- серединой той дуги второй окружности, которая
лежит вне треугольника BOC (см. задачу 2.93, а)).
Четырехугольник ABCD описанный тогда и только тогда, когда точки M
и N совпадают.
3.7. Пусть R- точка касания вневписанной окружности со
стороной BD, P и Q- точки пересечения отрезка MN с BC
и CD соответственно (рис. 3.9). Так как РDMQ = РBPN,
РDQM = РBNP и РDMQ = РBNP, то
треугольники MDQ,PBN и PCQ равнобедренные. Поэтому CP = CQ,DQ = DM = DR и BP = BN = BR. Следовательно, P,Q и R- точки касания
вписанной окружности треугольника BCD с его сторонами (см.
задачу 5.1).
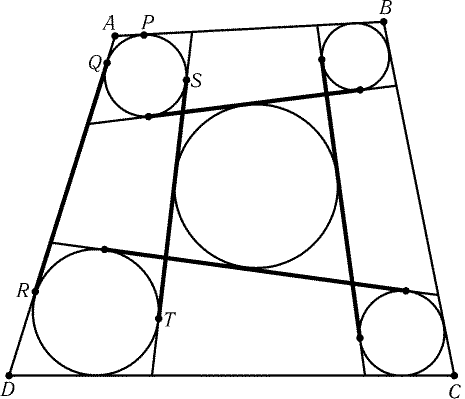
Рис. 3.10
3.8. Обозначим некоторые точки касания так, как показано на
рис. 3.10. Сумма длин одной пары противоположных сторон среднего
четырехугольника равна сумме длин пары других его сторон.
Продолжим стороны этого четырехугольника до точек касания
с вписанными окружностями остальных четырехугольников (ST-
один из полученных отрезков). При этом обе суммы длин пар
противоположных отрезков увеличатся на одно и то же число.
Каждый из полученных отрезков является общей касательной к паре
«угловых» окружностей; его можно заменить на равную ему по
длине другую общую внешнюю касательную (т. е. ST заменить на QR).
Для доказательства равенства AB + CD = BC + AD остается
воспользоваться равенствами вида AP = AQ.
3.9. Пусть P- точка пересечения диагоналей выпуклого
четырехугольника ABCD. Четырехугольник ABCD вписанный тогда и
только тогда, когда DAPB ~ DDPC, т. е. PA · PC = PB · PD. Так как четырехугольники ALBN и AMBK
вписанные, то PL · PN = PA · PB = PM · PK. Поэтому
четырехугольник KLMN вписанный.
-
3.10.
-
Пусть O- точка пересечения прямой AB и
отрезка MN. Тогда OM2 = OA · OB = ON2, т. е. OM = ON.
-
3.11.
-
Пусть для определенности лучи OA и BC сонаправлены;
M- точка пересечения прямых KL и OA. Тогда РLOM = РLCB = РOKM, а значит, DKOM ~ DOLM.
Следовательно, OM : KM = LM : OM, т. е. OM2 = KM · LM.
Кроме того, MA2 = MK · ML. Поэтому MA = OM.
-
3.12.
-
Пусть O- точка пересечения диагоналей AC и BD.
Тогда MO · OC = BO · OD. Тогда как OC = OA и BO = OD, то MO · OA = BO2 и MO · OA = DO2. Эти равенства означают, что OB
касается описанной окружности треугольника ABM и OD касается
описанной окружности треугольника ADM.
-
3.13.
-
Пусть C- точка пересечения прямой AB с описанной
окружностью треугольника BMN, отличная от точки B; AP-
касательная к окружности S. Тогда AB · AC = AM · AN = AP2, а
значит, AC = AP2/AB т. е. точка C одна и та же для всех прямых l.
Замечание.
Следует исключить случай, когда длина касательной, проведенной из A
к S, равна AB.
-
3.14.
-
Ясно, что MC2 = MP · MQ = MA · MB, причем точка M
лежит на луче AB, если AC > BC, и на луче BA, если AC < BC. Пусть
для определенности точка M лежит на луче AB.
Тогда (MB + BC)2 = (MB + BA) · MB. Следовательно,
MB = BC2/(AB – 2BC), а значит, положение точки M не зависит от выбора
окружности Sў.
-
3.15.
-
Пусть M- точка пересечения прямой CD и
касательной к окружностям в точке A. Тогда MC = MA = MD. Поэтому
точка A лежит на окружности с диаметром CD.
-
3.16.
-
Точки O1,A и O2 лежат на одной прямой,
поэтому РA2AO2 = РA1AO1. Треугольники AO2A2
и AO1A1 равнобедренные, поэтому РA2AO2 = РAA2O2
и РA1AO1 = РAA1O1. Следовательно,
РAA2O2 = РAA1O1 т. е. O1A1||O2A2.
-
3.17.
-
Пусть O1,O2 и O3- центры
окружностей S1,S2 и S3; A,B,C- точки касания
окружностей S2 и S3, S3 и S1, S1 и S2; A1
и B1- точки пересечения прямых CA и CB с окружностью S3.
Согласно предыдущей задаче B1O3||CO1 и A1O3||CO2. Точки O1,C и O2 лежат на одной прямой, поэтому
точки A1,O3 и B1 тоже лежат на одной прямой, т. е. A1B1
диаметр окружности S3.
-
3.18.
-
Пусть A1,A2 и B- точки касания окружностей с
центрами O и O1, O и O2, O1 и O2,.
Тогда O1O2 = O1B + BO2 = O1A1 + O2A2. Поэтому
OO1 + OO2 + O1O2 = (OO1 + O1A1) + (OO2 + O2A2) = OA1 + OA2 = 2R.
-
3.19.
-
Пусть O,O1 и O2- центры окружностей S,S1
и S2; C- общая точка окружностей S1 и S2, лежащая на
отрезке AB. Треугольники AOB, AO1C и CO2B равнобедренные,
поэтому OO1CO2- параллелограмм и OO1 = O2C = O2B, а значит,
AO = AO1 + O1O = AO1 + O2B.
-
3.20.
-
Пусть O1 и O2- центры окружностей S1
и S2; X- вторая точка пересечения прямой AB с
окружностью S2. Квадрат искомой длины касательной равен BA · BX. Так как AB : BX = O1A : O1O2, то
AB · BX = AB2 · O1O2/R = a2(R±r)/R, где знак минус берется
в случае внутреннего касания.
-
3.21.
-
Пусть O,O1 и O2 — центры окружностей с
диаметрами AB,AC и BC. Достаточно проверить, что KO = OL. Докажем,
что DO1KO = DO2OL. В самом деле, O1K = AC/2 = O2O,
O1O = BC/2 = O2L и РKO1O = РOO2L = 180° – 2a,
где a — угол между прямыми KL и AB.
-
3.22.
-
Пусть Oi- центр окружности Si, Ai-
точка касания окружностей Si и Si + 1.
Четырехугольник O1O2O3O4 выпуклый; пусть a1,a2,a3
и a4- величины его углов. Легко проверить, что РAi – 1AiAi + 1 = (ai + ai + 1)/2, поэтому
РA1 + РA3 = (a1 + a2 + a3 + a4)/2 = РA2 + РA4.
-
3.23.
-
а) Пусть A1,B1 и C1- проекции точек A,B
и C на прямую l; C2- проекция точки C на прямую AA1.
По теореме Пифагора CC22 = AC2 – AC22, т. е.
A1C12 = (a + c)2 – (a – c)2 = 4ac. Аналогично B1C12 = 4bc
и A1B12 = 4ab. Так как A1C1 + C1B1 = A1B1,
то
,
т. е. 1/Цb + 1/Цa = 1/Цc.
б) Пусть A,B,C — центры «внешних» окружностей, D — центр
«внутренней» окружности (рис. 3.11). Полупериметр треугольника BDC
равен b + c + d, поэтому
|
cos 2 |
ж
и
|
BDC
2
|
ц
ш
|
= |
d(b + c + d)
(b + d)(c + d)
|
,
sin 2 |
ж
и
|
BDC
2
|
ц
ш
|
= |
bc
(b + d)(c + d)
|
|
|
(см. задачу 12.13). Если aў + bў + gў = 180°,
то sin 2aў + sin 2bў – sin 2gў + 2 sin bўgў cos aў = 0
(это утверждение эквивалентно теореме косинусов). Подставив в эту
формулу значения aў = РBDC/2, bў = РADC/2
и gў = РADB/2, получим
|
|
bc
(b + d)(c + d)
|
– |
ac
(a + d)(c + d)
|
– |
ab
(a + d)(b + d)
|
+ 2 |
(a + d)(b + d)(c + d)
|
= 0, |
|
т. e.
|
|
a + d
a
|
– |
b + d
b
|
– |
c + d
c
|
+ 2 |
ж
Ц
|
|
= 0. |
|
Разделив на d, имеем
| a – b – g – d + 2 |
Ц
|
bg + gd + db
|
= 0
|
. Поэтому
(a + b + g + d)2 = (a – b – g – d)2 + 4(ab + ag + ad) = 4(bg + gd + db) + 4(ab + ag + ad) = 2(a
> + d)2 – 2(a2 + b2 + g2 + d2),
т. е. 2(a2 + b2 + g2 + d2) = (a + b + g + d)2.
-
3.24.
-
Пусть A1,B1 и C1- центры данных окружностей
(рис. 3.12). Тогда A1BC1H- ромб, а значит, BA1||HC1. Аналогично B1A||HC1, поэтому B1A||BA1
и B1ABA1- параллелограмм.
а) Так как A1B1^CH и A1B1||AB, то AB^CH.
Аналогично доказывается, что BC^AH и CA^BH.
б) Так же, как было доказано, что B1A||BA1, можно доказать,
что B1C||BC1 и A1C||AC1; кроме того, длины всех
этих шести отрезков равны R. Достроим треугольник BA1C до
ромба BA1CO. Тогда AB1CO тоже ромб. Поэтому AO = BO = CO = R,
т. e. O- центр описанной окружности треугольника ABC, и ее
радиус равен R.
-
3.25.
-
Легко проверить, что
ИAB1±ИB1A1 = ИAC1 + ИC1A1,
ИBC1 + ИC1B1 = ИBA1±ИB1A1
и ИC1A1±ИCA1 = ИC1B1±ИB1C, где знак
минус берется только в случае б . Складывая эти равенства,
получаем ИAB1 + ИBC1±ИCA1 = ИAC1 + ИBA1±ИCB1.
С другой стороны, удвоенные величины углов треугольника ABC
равны ИBA1±ИCA1, ИAB1±ИCB1
и ИBC1 + ИAC1, а их сумма равна 360°.
-
3.26.
-
Так как ИAP + ИBP + ИPQ = 180° (см.
задачу 3.25), то ИAB = 180° – ИPQ.
Аналогично ИCD = 180° – ИPQ,
т. е. ИAB = ИCD, а значит, AB = CD. Кроме того,
PQ^AB и PQ^CD (см. задачу 3.24),
поэтому AB||CD.
-
3.27.
-
Точки M,B и C лежат на окружности с диаметром AO.
Кроме того, хорды OB и OC этой окружности равны.
-
3.28.
-
Точки B и X лежат на окружности с диаметром KO,
поэтому РXKO = РXBO.
Аналогично РXLO = РXCO. Так как РXBO = РXCO,
то треугольник KOL равнобедренный, причем OX- его высота.
-
3.29.
-
Достаточно проверить, что AK · AL = AM · AO. В
самом деле, тогда точки K,L,M и O лежат на одной окружности, и
поэтому РMKO = РMLO. Так как DAOP ~ D
APM, то AM · AO = AP2; ясно также, что AK · AL = AP2.
-
3.30.
-
Пусть O- центр окружности; точки Dў и Eў
симметричны точкам D и E относительно прямой AO. Согласно
задаче 28.7 прямые EDў и EўD пересекаются в точке M.
Поэтому РBDM = РEBM и РBEM = РDBM, а значит,
DBDM ~ DEBM
Следовательно, BM : DM = EM : BM. Кроме того, если
прямая ED разделяет точки B и M, то РDME = И
DE = 2РDCE.
Из равенства РBEM = РDBM следует, что РBEM = РDBC = РDEC.
-
3.31.
-
а) Так как DKAB ~ DKBC,
то AB : BC = KB : KC. Аналогично AD : DC = KD :
KC. Учитывая, что KB = KD, получаем требуемое.
б) Задача сводится к предыдущей, так как
|
|
PQ
BQ
|
= |
sin PBQ
sin BPQ
|
= |
sin ABD
sin KBA
|
= |
sin ABD
sin ADB
|
= |
AD
AB
|
,
|
QR
BQ
|
= |
CD
CB
|
. |
|
-
3.32.
-
Опустим из центра O окружности S перпендикуляр OM
на прямую l. Докажем, что точка X, в которой пересекаются AB
и OM, остается неподвижной. Точки A,B и M лежат на окружности
с диаметром PO. Поэтому РAMO = РABO = РBAO, а значит,
DAMO ~ DXAO, так как угол при вершине O
у этих треугольников общий. Следовательно, AO : MO = XO :
AO, т. е. OX = OA2/MO- постоянная величина.
-
3.33.
-
Так как РOBP = РOAB = РOCB,
то DOBP ~ DOCB, а значит, OB2 = OP · OC.
Проведем из точки C касательную CD к окружности S1.
Тогда OD2 = OB2 = OP · OC. Следовательно,
DODC ~ DOPD и РOPD = РODC = 90°.
-
3.34.
-
Прямые BC и AD являются высотами треугольника APB,
поэтому прямая PQ, проходящая через точку Q их пересечения,
перпендикулярна прямой AB.
-
3.35.
-
Обозначим точки пересечения прямых AC и BD, BC
и AD через K и K1 соответственно. Согласно предыдущей
задаче KK1^AB, поэтому достаточно доказать, что точка
пересечения касательных в точках C и D лежит на прямой KK1.
Докажем, что касательная в точке C проходит через
середину отрезка KK1. Пусть M- точка пересечения касательной
в точке C и отрезка KK1. Стороны острых углов ABC и CKK1
соответственно перпендикулярны, поэтому они равны. Аналогично РCAB = РCK1K. Ясно также, что РKCM = РABC, поэтому
треугольник CMK равнобедренный. Аналогично треугольник CMK1
равнобедренный и KM = CM = K1M, т. е. M- середина отрезка KK1.
Аналогично доказывается, что касательная в точке D проходит
через середину отрезка KK1.
-
3.36.
-
а) Прямая AC пересекает окружность в точках A
и A1, прямая BC — в точках B и B1. Если A = A1
(или B = B1), то прямая AC (или BC) — искомый перпендикуляр. Если
же это не так, то AB1 и BA1 являются высотами треугольника ABC
и искомая прямая — это прямая, проходящая через точку C и точку
пересечения прямых AB1 и BA1.
б) Возьмем точку C1, не лежащую на окружности, и опустим
из нее перпендикуляр на AB. Пусть он пересекается с окружностью
в точках D и E. Построим точку P пересечения прямых DC и AB,
а затем точку F пересечения прямой PE с окружностью. При
симметрии относительно AB точка C переходит в точку F.
Поэтому CF — искомый перпендикуляр.
-
3.37.
-
Так как PA^ObOc, то прямая PA проходит через
точку Oa тогда и только тогда, когда прямая POa проходит через
точку пересечения высот треугольника OaObOc. Аналогичные
утверждения верны и для точек B и C. Из условия задачи следует,
что P- точка пересечения высот треугольника OaObOc, а
значит, POc^OaOb.
-
3.38.
-
Пусть 2a и 2b- длины катетов, 2c- длина
гипотенузы. Сумма площадей «луночек» равна pa2 + pb2 + SABC – pc2. Ясно, что p(a2 + b2 – c2) = 0.
-
3.39.
-
Доказательство достаточно провести для каждой из четырех
частей, на которые диаметры делят исходный круг (рис. 3.13).
Рассмотрим в круге сегмент, отсекаемый хордой, на которую опирается
центральный угол 90°; пусть S и s- площади таких
сегментов для исходного и четырех построенных кругов соответственно.
Ясно, что S = 4s. Остается заметить, что площадь части с одинарной
штриховкой равна S – 2s = 2s, а площадь части с двойной штриховкой
равна 2s.
-
3.40.
-
Обозначим точки пересечения окружностей, построенных
на отрезках OB и OC, OA и OC, OA и OB, через A1,B1,C1
соответственно (рис. 3.14). РOA1B = РOA1C = 90°,
поэтому точки B,A1 и C лежат на одной прямой, а так как окружности
имеют одинаковые радиусы, то BA1 = A1C. Точки A1,B1,C1 являются
серединами сторон треугольника ABC, поэтому BA1 = C1B1
и BC1 = A1B1. Так как круги имеют одинаковый радиус, то равные
хорды BA1 и C1B1 отсекают от кругов части равной площади, а
равные хорды C1B и B1A1 также отсекают от кругов части равной
площади. Поэтому площадь криволинейного треугольника A1B1C1 равна
площади параллелограмма A1B1C1B, т. е. равна половине площади
треугольника ABC.
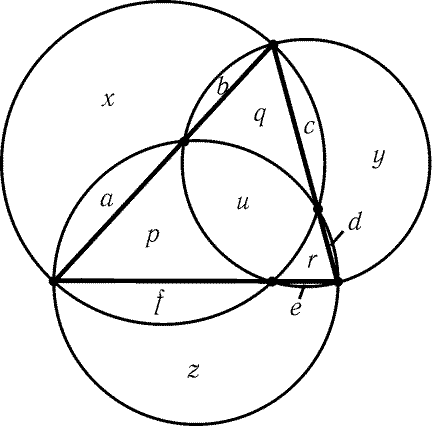
Рис. 3.15
3.41. Рассматриваемые окружности проходят через основания
высот треугольника, а значит, точки их пересечения лежат на
сторонах треугольника. Пусть x,y,z и u- площади рассматриваемых
криволинейных треугольников; a,b,c,d,e и f- площади сегментов,
отсекаемых от окружностей сторонами треугольника; p,q и r-
площади частей треугольника, лежащих вне внутреннего криволинейного
треугольника (рис. 3.15). Тогда x + (a + b) = u + p + q + (c + f),y + (c + d) = u + q + r + (e + b) и z + (e + f) = u + r + p + (a + d). Складывая эти равенства,
получаем x + y + z = 2(p + q + r + u) + u.
3.42. а) Пусть O и O1- центры окружностей S
и S1. Треугольники MO1N и PON равнобедренные, причем РMO1N = РPON. Следовательно, точки P,M и N лежат на одной
прямой.
б) Ясно, что PQ2 = PM · PN = PM · (PM + MN). Пусть K-
середина хорды AB. Тогда PM2 = PK2 + MK2 и PM · MN = AM · MB = AK2 – MK2. Поэтому PQ2 = PK2 + AK2 = PA2.
-
3.43.
-
Согласно задаче 3.42, б) BE = BD. Поэтому РDAE + РADE = РDEB = РBDE = РBDC + РCDE.
А так как РDAB = РBDC, то РADE = РCDE.
-
3.44.
-
Пусть O1 и O2- центры вписанных окружностей,
CP и CQ- касательные к ним.
Тогда CO12 = CP2 + PO12 = CP2 + O1M2 и, так как CQ = CA = CP
(задача 3.42, б)), CO22 = CQ2 + QO22 = CP2 + O2M2. Следовательно,
CO12 – CO22 = MO12 – MO22, а значит, прямая CM
перпендикулярна O1O2 (см. задачу 7.6). Поэтому прямая MN проходит
через точку C.
Замечание.
Если окружности не пересекаются, а касаются, утверждение остается
верным; в этом случае прямую MN нужно заменить на касательную к
окружностям в их общей точке.
-
3.45.
-
Пусть РLAB = a и РLBA = b (a + b = 90°).
Согласно задаче 3.42, б) AB1 = AL, поэтому
РAB1L = (90° – a)/2. Аналогично
РBA1L = (90° – b)/2. Следовательно,
РA1LB1 = (a + b)/2 = 45°.
-
3.46.
-
Пусть A1 и B1- середины дуг BC и AC;
O- центр вписанной окружности. Тогда A1B1^CO (см.
задачу 2.19, а) и MN^CO, а значит, MN||A1B1. Будем
перемещать точки Mў и Nў по лучам CA и CB так,
что MўNў||A1B1. Лишь при одном положении точек Mў и Nў
точка L, в которой пересекаются прямые B1Mў и A1Nў, попадает на
описанную окружность треугольника ABC. С другой стороны, если
отрезок MN проходит через точку O, точка L попадает на эту
окружность (см. задачу 2.50).
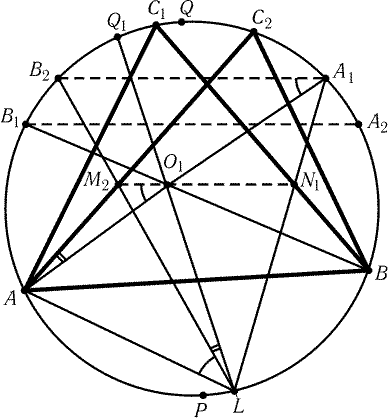
Рис. 3.16
3.47. Решение этой задачи обобщает решение предыдущей задачи.
Достаточно доказать, что центр O1 вписанной окружности
треугольника ABC1 лежит на отрезке M2N1. Пусть A1
и A2- середины дуг BC1 и BC2, B1 и B2- середины
дуг AC1 и AC2; PQ- диаметр окружности S,
перпендикулярный хорде AB, причем Q и C1 лежат по одну сторону
от прямой AB. Точка O1 является точкой пересечения хорд AA1
и BB1, а точка L касания окружностей S и S1 является точкой
пересечения прямых A1N1 и B2M2 (рис. 3.16). Пусть РC1AB = 2a,РC1BA = 2b, РC1AC2 = 2j.
Тогда ИA1A2 = 2j = ИB1B2, т. е. A1B2||
||B1A2. Угол между хордами A1B2 и BC1
равен (ИB2C1 + ИA1B)/2 = b – j + a, а угол между хордами BC1
и AC2
равен (ИC1C2 + ИAB)/2 = 2j + 180° – 2a – 2b.
Поэтому хорда M2N1 образует с касательными BC1 и AC2 равные
углы a + b – j, а значит, M2N1||A1B2.
Предположим теперь, что точки M2ў и N1ў перемещаются по
хордам AC2 и BC1 так, что M2ўN1ў||A1B2. Пусть
прямые A1N1ў и B2M2ў пересекаются в точке Lў. Точка Lў
лежит на окружности S лишь при одном положении точек M2ў и N1ў.
Поэтому достаточно указать на дуге AB такую точку L1, что
если M2ўў,N1ўў- точки пересечения хорд AC2 и L1B2,
BC1 и L1A1, то M2ўўN1ўў||A1B2 и точка O1 лежит
на отрезке M2ўўN1ўў. Пусть Q1- такая точка окружности S,
что 2Р(PQ,PQ1) = Р(PC2,PC1), и L1- точка
пересечения прямой Q1O1 с окружностью S. Докажем, что точка L1
искомая. Так как ИB1Q = 2a,
то ИB2Q1 = 2(a – 2j) = ИC2A1. Поэтому
четырехугольник AM2ўўO1L1 вписанный,
а значит, РM2ўўO1A = РM2ўўL1A = РB2A1A,
т. е. M2ўўO1||B2A1. Аналогично N1ўўO1||B2A1.
-
3.48.
-
Пусть окружности с центрами O1 и O2 проходят через
точку A. Радиусы O1A и O2A перпендикулярны касательным
к окружностям в точке A, поэтому окружности ортогональны тогда
и только тогда, когда РO1AO2 = 90°,
т. е. O1O22 = O1A2 + O2A2.
-
3.49.
-
Пусть A1,B1 и C1- центры данных окружностей,
причем точки A,B и C лежат на отрезках B1C1,C1A1 и A1B1
соответственно. Так как A1B = A1C,B1A = B1C и C1A = C1B, то A,B
и C- точки касания вписанной окружности треугольника A1B1C1
с его сторонами (см. задачу 5.1). Таким образом, радиусы A1B,B1C
и C1A данных окружностей касаются описанной окружности
треугольника ABC.
-
3.50.
-
Легко проверить, что угол поворота от
вектора
до вектора
(против часовой стрелки)
равен 2Р(AB,AMi). Ясно также,
что Р(AB,AM1) = Р(AB,AM2).
-
3.51.
-
Проведем через точку P другую прямую, пересекающую
окружность в точках A1 и B1. Тогда D
PAA1 ~ DPB1B, поэтому PA : PA1 = PB1 : PB.
-
3.52.
-
Проведем через точку P касательную PC. D
PAC ~ DPCB, поэтому PA : PC = PC : PB.
-
3.53.
-
Пусть прямая, проходящая через точку P и центр
окружности, пересекает окружность в точках A и B. Тогда PA = d + R
и PB = |d – R|. Поэтому PA · PB = |d2 – R2|. Ясно также, что
величина d2 – R2 и степень точки P относительно окружности S
имеют одинаковые знаки.
-
3.54.
-
Пусть R1 и R2- радиусы окружностей. Рассмотрим
систему координат, в которой центры окружностей имеют
координаты ( – a,0) и (a,0). Согласно задаче 3.53 степени точки с
координатами (x,y) относительно данных окружностей
равны (x + a)2 + y2 – R12 и (x – a)2 + y2 – R22 соответственно.
Приравнивая эти выражения, получаем x = (R12 – R22)/4a. Это уравнение
задает прямую, перпендикулярную отрезку, соединяющему центры
окружностей.
-
3.55.
-
Степени точки пересечения окружностей относительно
каждой из них равны нулю, поэтому она лежит на радикальной
оси. Если точек пересечения две, то они однозначно задают
радикальную ось.
-
3.56.
-
Так как центры окружностей не лежат на одной прямой,
радикальная ось первой и второй окружностей пересекается с радикальной
осью второй и третьей окружностей. Степени точки
пересечения относительно всех трех окружностей равны, поэтому
она лежит на радикальной оси первой и третьей окружностей.
-
3.57.
-
Согласно задаче 3.55 прямые, содержащие хорды, являются
радикальными осями. Согласно задаче 3.56 радикальные оси пересекаются
в одной точке, если центры окружностей не лежат на одной
прямой. В противном случае они перпендикулярны этой прямой.
-
3.58.
-
Пусть O1 и O2- центры данных окружностей,
r1 и r2- их радиусы. Окружность S радиуса r с центром O
ортогональна окружности Si тогда и только тогда,
когда r2 = OOi2 – ri2, т. е. квадрат радиуса окружности S равен
степени точки O относительно окружности Si. Поэтому множеством
центров искомых окружностей является множество тех точек радикальной
оси, степени которых относительно данных окружностей положительны.
-
3.59.
-
а) Указанные точки лежат на радикальной оси.
б) Точки касания внешних касательных с окружностями являются
вершинами трапеции ABCD с основанием AB. Середины боковых
сторон AD и BC принадлежат радикальной оси, поэтому середина O
диагонали AC тоже принадлежит радикальной оси. Если прямая AC
пересекает окружности в точках A1 и C1, то OA1 · OA = OC1 · OC, а значит, OA1 = OC1 и AA1 = CC1.
-
3.60.
-
а) Пусть SA и SB- окружности с
диаметрами AA1 и BB1; S- окружность с диаметром AB.
Общими хордами окружностей S и SA, S и SB являются
высоты AHa и BHb, поэтому они (или их продолжения) пересекаются в
точке H. Согласно задаче 3.57 общая хорда окружностей SA и SB
проходит через точку пересечения хорд AHa и BHb.
б) Общая хорда окружностей SA и SB проходит через точку
пересечения прямых A1Ha и B1Hb (т. е. через точку C) тогда
и только тогда, когда CB1 · CHb = CA1 · CHa (длины отрезков
следует считать ориентированными). Так как CHb = (a2 + b2 – c2)/2b
и CHa = (a2 + b2 – c2)/2a, приходим к соотношению CB1/b = CA1/a.
-
3.61.
-
Проведем в треугольнике CDE высоты CC1 и DD1;
пусть H- точка их пересечения. Окружности с диаметрами AC и BD
проходят через точки C1 и D1 соответственно, поэтому степень
точки H относительно каждой из этих окружностей равна ее степени
относительно окружности с диаметром CD (эта окружность проходит через
точки C1 и D1). Аналогично доказывается, что степени точки H
относительно окружностей с диаметрами AC,BD и EF равны, т. е.
радикальные оси этих окружностей проходят через точку H. Для точек
пересечения высот остальных трех треугольников доказательство
проводится аналогично.
Замечание.
Центры рассматриваемых окружностей лежат на прямой Гаусса (см.
задачу 4.55), поэтому их общая радикальная ось перпендикулярна прямой
Гаусса.
-
3.62.
-
Прямые A1A2,B1B2 и C1C2 пересекаются в
некоторой точке O (см. задачу 3.57). Так как D
A1OB2 ~ DB1OA2, то A1B2 : A2B1 = OA1 :
OB1. Аналогично B1C2 : B2C1 = OB1 : OC1
и C1A2 : C2A1 = OC1 : OA1. Перемножая эти равенства,
получаем требуемое.
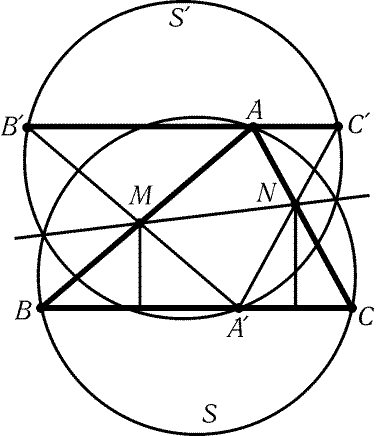
Рис. 3.17
3.63. Обозначим через Bў и Cў точки пересечения
прямых AўM и AўN с прямой, проведенной через точку A
параллельно BC (рис. 3.17). Так как треугольники AўBM и AўNC
равнобедренные, то DABC = DAўBўCў. Поскольку AM · BM = AўM · BўM, степени точки M относительно окружностей S
и Sў, описанных около треугольников ABC и AўBўCў соответственно,
равны. Это верно и для точки N, поэтому прямая MN является
радикальной осью окружностей S и Sў. Окружности S и Sў имеют
одинаковые радиусы, поэтому их радикальная ось является их осью
симметрии. Точка Aў, лежащая на окружности Sў, при симметрии
относительно прямой MN переходит в точку, лежащую на окружности S.
3.64. Пусть AC и BD- касательные; E и K-
точки пересечения прямых AC и BD, AB и CD; O1 и O2-
центры окружностей (рис. 3.18). Так как AB^O1E, O1E^O2E
и O2E^CD, то AB^CD, а значит, K- точка
пересечения окружностей S1 и S2 с диаметрами AC и BD.
Точка K лежит на радикальной оси окружностей S1 и S2; остается
проверить, что этой радикальной осью является прямая O1O2.
Радиусы O1A и O1B являются касательными к S1 и S2, поэтому
точка O1 лежит на радикальной оси. Аналогично точка O2 лежит на
радикальной оси.
-
3.65.
-
Обозначим данные окружности через S1,…,Sn. Для
каждой окружности Si рассмотрим множество Mi, состоящее из тех
точек X, для которых степень относительно Si не больше степеней
относительно S1,…,Sn. Тогда Mi- выпуклое множество. В
самом деле, пусть Mij- множество точек X, для которых
степень относительно Si не больше степени относительно Sj.
Mij является полуплоскостью, состоящей из точек, лежащих по одну
сторону с окружностью Si от радикальной оси окружностей Si
и Sj. Множество Mi является пересечением выпуклых
множеств Mij, поэтому оно само выпуклое. Кроме того, поскольку
каждое из множеств Mij содержит окружность Si, то Mi
содержит Si. Так как для каждой точки плоскости какая-то из
степеней относительно S1,…,Sn является наименьшей,
множества Mi покрывают всю плоскость. Рассматривая те части
множеств Mi, которые лежат внутри исходного многоугольника, получаем
требуемое разбиение.
-
3.66.
-
а) Точки B1 и C1 лежат на окружности с
диаметром BC, поэтому степени точки Aў относительно описанных
окружностей треугольников A1B1C1
и ABC равны степени точки Aў
относительно этой окружности. Значит, точка Aў лежит на радикальной оси
окружности Эйлера и описанной окружности треугольника ABC.
Для точек Bў и Cў доказательство аналогично.
б) Рассмотрим треугольник A1B1C1, образованный внешними
биссектрисами треугольника ABC (треугольник A1B1C1 остроугольный).
Согласно задаче а) точки Aў,Bў и Cў
лежат на радикальной
оси описанных окружностей треугольников ABC и A1B1C1.
Радикальная ось этих окружностей перпендикулярна прямой, соединяющей
их центры, т. е. прямой Эйлера треугольника A1B1C1. Остается
заметить, что точка пересечения высот треугольника A1B1C1 является
точкой пересечения биссектрис треугольника ABC (см. задачу 1.57, а)).
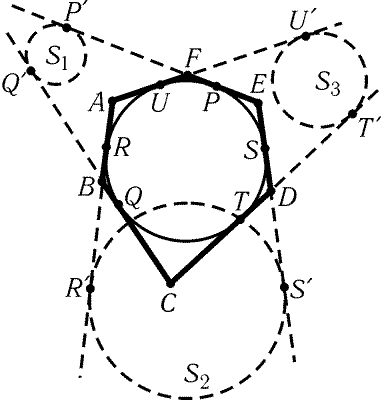
Рис. 3.19
3.67. Пусть выпуклый шестиугольник ABCDEF касается окружности
в точках R,Q,T,S,P,U (точка R лежит на AB, Q- на BC и
т. д.).
Выберем произвольное число a > 0 и построим на прямых BC и EF
точки Qў и Pў так, что QQў = PPў = a, а векторы
и
сонаправлены с векторами
и
.
Аналогично строим точки Rў,Sў,Tў,Uў (рис. 3.19; RRў = SSў = TTў = UUў = a).
Построим окружность S1, касающуюся прямых BC и EF в точках Qў
и Pў. Аналогично построим окружности S2 и S3.
Докажем, что точки B и E лежат на радикальной оси окружностей S1
и S2. BQў = QQў – BQ = RRў – BR = BRў (если QQў < BQ,
то BQў = BQ – QQў = BR – RRў = BRў) и EPў = EP + PPў = ES + SSў = ESў. Аналогично
доказывается, что прямые FC и AD являются радикальными осями
окружностей S1 и S3, S2 и S3 соответственно. Так как
радикальные оси трех окружностей пересекаются в одной точке,
прямые AD,BE и CF пересекаются в одной точке.
-
3.68.
-
Пусть Ai- точка касания окружностей Si
и Si + 1, X- точка пересечения прямых A1A4 и A2A3.
Тогда X- точка пересечения общих внешних касательных к
окружностям S2 и S4 (см. задачу 5.66). А так как
четырехугольник A1A2A3A4 вписанный (задача 3.22), то XA1 · XA4 = XA2 · XA3, а значит, точка X лежит на радикальной оси
окружностей S1 и S3.
-
3.69.
-
а) Рассмотрим систему координат с началом O в середине
отрезка, соединяющего центры окружностей, а ось Ox направим
вдоль этого отрезка. Пусть точка P имеет координаты (x,y);
R и r — радиусы окружностей S1 и S2; a = d/2.
Тогда (x + a)2 + y2 = R2
и p = (x – a)2 + y2 – r2 = ((x + a)2 + y2 – R2) – 4ax – r2 + R2 = R2 – r2 – 4ax.
Пусть точка A имеет координаты (x0,y0).
Тогда (x0 + a)2 + y02 – R2 = (x0 – a)2 + y02 – r2,
т. е. x0 = (R2 – r2)/4a. Поэтому 2dh = 4a|x0 – x| = |R2 – r2 – 4ax| = |p|.
б) Пусть d — расстояние между центрами описанных окружностей
треугольников ACD и BCD; ha и hb- расстояния от точек A
и B до прямой CD. Согласно задаче а) |pa| = 2dha и |pb| = 2dhb.
Учитывая, что SBCD = hbCD/2 и SACD = haCD/2, получаем требуемое.

 Глава 3. Задачи для самостоятельного решения |
Глава 3. Задачи для самостоятельного решения | 

 Глава 3. Задачи для самостоятельного решения |
Глава 3. Задачи для самостоятельного решения | 


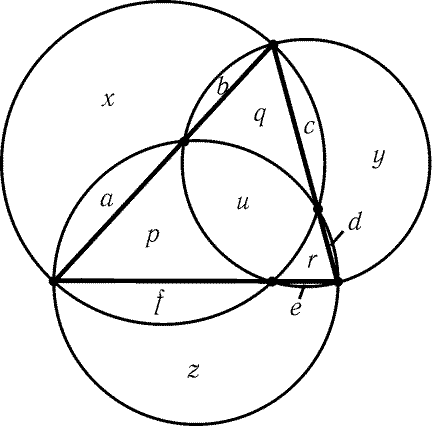


 Глава 3. Задачи для самостоятельного решения |
Глава 3. Задачи для самостоятельного решения | 
