| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
10.1.
-
Пусть медианы AA1 и BB1 пересекаются в точке M.
Так как BC > AC, то точки A и C лежат по одну сторону
от серединного перпендикуляра к отрезку AB, а значит, по ту же сторону
лежат медиана CC1 и ее точка M. Следовательно, AM < BM,
т. е. ma < mb.
-
10.2.
-
Предположим, например, что a > b. Тогда ma < mb
(задача 10.1). А так как четырехугольник A1MB1C описанный,
то
,
т. е. (a – b)/2 = (ma – mb)/3. Получено противоречие.
-
10.3.
-
Пусть, например, BC > AC. Тогда MA < MB (см.
задачу 10.1), поэтому BC + MB + MC > AC + MA + MC.
-
10.4.
-
а) Так как c Ј a + b,
то c2 Ј (a + b)2 = a2 + b2 + 2ab Ј 2(a2 + b2).
б) Пусть M- точка пересечения медиан треугольника ABC. Согласно
задаче а) MA2 + MB2 і AB2/2, т. е.
.
-
10.5.
-
а) Пусть M- точка пересечения медиан, O-
центр описанной окружности треугольника ABC. Тогда
| AO2 + BO2 + CO2 = ( |
®
AM
|
+ |
®
MO
|
)2 + ( |
®
BM
|
+ |
®
MO
|
)2 + ( |
®
CM
|
+ |
®
MO
|
)2 = AM2 + BM2 + CM2 + 2( |
®
AM
|
+ |
®
BM
|
+ |
®
CM
|
, |
®
MO
|
) + 3MO2
|
. Так как
,
то AO2 + BO2 + CO2 = AM2 + BM2 + CM2 + 3MO2 і AM2 + BM2 + CM2,
т. е. 3R2 і 4(ma2 + mb2 + mc2)/9.
б) Достаточно заметить, что (ma + mb + mc)2 Ј 3(ma2 + mb2 + mc2)
(см. приложение к гл. 9).
-
10.6.
-
Формулу Герона можно переписать в виде
16S2 = 2a2b2 + 2a2c2 + 2b2c2 – a4 – b4 – c4. А так как
mc2 = (2a2 + 2b2 – c2)/4 (задача 12.11, а)), то неравенства
mc2 Ј ((a2 + b2)/2c)2 и mc2 > ((a2 – b2)/2c)2 эквивалентны
неравенствам 16S2 Ј 4a2b2 и 16S2 > 0 соответственно.
-
10.7.
-
Пусть y = a2 + b2 + c2 и y1 = ma2 + mb2 + mc2.
Тогда 3y = 4y1 (задача 12.11, б)), y < 2x (задача 9.7)
и 2x1 + y1 < 2x + y, так как (ma + mb + mc)2 < (a + b + c)2 (см.
задачу 9.2). Сложив неравенство 8x1 + 4y1 < 8x + 4y
с равенством 3y = 4y1, получим 8x1 < y + 8x < 10x, т. е. x1/x < 5/4.
Пусть M- точка пересечения медиан треугольника ABC. Достроим
треугольник AMB до параллелограмма AMBN. Применив
к треугольнику AMN доказанное утверждение, получим (x/4)/(4x1/9) < 5/4, т. е. x/x1 < 20/9.
-
10.8.
-
Ясно, что ha Ј b, hb Ј c, hc Ј a, причем
по крайней мере одно их этих неравенств строгое.
Поэтому ha + hb + hc < a + b + c.
-
10.9.
-
Пусть ha > 1 и hb > 1. Тогда a і hb > 1.
Поэтому S = aha/2 > 1/2.
-
10.10.
-
По условию BH і AC, а так как перпендикуляр короче
наклонной, то BH і AC і AM. Аналогично AM і BC і BH.
Поэтому BH = AM = AC = BC. Поскольку AC = AM, то отрезки AC и AM
совпадают, т. е. РC = 90°, а так как AC = BC, то углы
треугольника ABC равны 45, 45, 90°.
-
10.11.
-
Ясно, что
|
1
ha
|
+ |
1
hb
|
= |
a + b
2S
|
= |
a + b
(a + b + c)r
|
|
и a + b + c < 2(a + b) < 2(a + b + c).
-
10.12.
-
Так как aha = 2S = r(a + b + c),
то
| ha = r |
ж
и
|
1 + |
b
a
|
+ |
c
a
|
ц
ш
|
|
. Сложив такие равенства
для ha,hb
и hc и воспользовавшись неравенством
, получим требуемое.
-
10.13.
-
Так как ha – hb = 2S(1/a – 1/b) = 2S(b – a)/ab и 2S Ј ab,
то ha – hb Ј b – a.
-
10.14.
-
Согласно задаче 12.21
. Кроме того,
.
-
10.15.
-
Так как 2sin bsin g
= cos (b – g) – cos (b + g) Ј 1 + cos a,
то
|
|
ha
a
|
= |
sin bsin g
sin a
|
Ј |
1 + cos a
2sin a
|
= |
1
2
|
ctg |
a
2
|
. |
|
-
10.16.
-
Так как b/2R = sin b, то после домножения на 2p
переходим к неравенству (a + b + c)(ha + hb + hc) Ј 3sin b(a2 + ac + c2). Вычитая из обеих частей 6S, получаем
a(hb + hc) + b(ha + hc) + c(ha + hb) Ј 3sin b(a2 + c2). Так как,
например, ahb = a2sin g
= a2c/2R, переходим к неравенству
a(b2 + c2) – 2b(a2 + c2) + c(a2 + b2) Ј 0. Для доказательства
последнего неравенства рассмотрим квадратный трехчлен f(x) = x2(a + c) – 2x(a2 + c2) + ac(a + c). Легко проверить, что f(a) = – a(a – c)2 Ј 0
и f(c) = – c(a – c)2 Ј 0. А так как коэффициент при x положителен
и a Ј b Ј c, то f(b) Ј 0.
-
10.17.
-
Согласно задаче 12.35, а) la2 = 4bcp(p – a)/(b + c)2.
Кроме того, 4bc Ј (b + c)2.
-
10.18.
-
Ясно, что ha/la = cos ((b – g)/2). Согласно
задаче 12.36, а)
|
2r/R = 8sin (a/2)sin (b/2)sin (g/2) = 4sin (a/2)[cos ((b – g)/2) – |
|
|
– cos ((b + g)/2)] = 4x(q – x), где x = sin (a/2) и q = cos ((b – g)/2). |
|
Остается заметить, что 4x(q – x) Ј q2.
-
10.19.
-
а) Согласно задаче 10.17 la2 Ј p(p – a). Складывая
три аналогичных неравенства, получаем требуемое.
б) Для любых чисел la,lb и lc справедливо
неравенство (la + lb + lc)2 Ј 3(la2 + lb2 + lc2).
-
10.20.
-
Достаточно доказать, что
|
Ц
|
p(p – a)
|
+ |
Ц
|
p(p – b)
|
+ mc Ј |
Ц
|
3p
|
|
.
Можно считать, что p = 1;
пусть x = 1 – a и y = 1 – b.
Тогда mc2 = (2a2 + 2b2 – c2)/4 = 1 – (x + y) + (x – y)2/4 = m(x,y).
Рассмотрим функцию
| f(x,y) = Цx + Цy + |
Ц
|
m(x,y)
|
|
. Нужно доказать,
что f(x,y) Ј Ц3 при x,y і 0 и x + y Ј 1.
Пусть
| g(x) = f(x,x) = 2Цx + |
Ц
|
1 – 2x
|
|
. Так как
,
то при возрастании x от 0 до 1/3 g(x) возрастает от 1 до Ц3,
а при возрастании x от 1/3 до 1/2 g(x) убывает от Ц3
до Ц2. Введем новые переменные d = x – y и q = Цx + Цy.
Легко проверить, что (x – y)2 – 2q2(x + y) + q4 = 0,
т. е. x + y = (d2 + q4)/2q2. Поэтому
|
f(x,y) = q + |
ж
Ц
|
|
1 – |
q2
2
|
– |
d2(2 – q2)
4q2
|
|
. |
|
Заметим теперь, что q2 = (Цx + Цy)2 Ј 2(x + y) Ј 2, т. е.
d2(2 – q2)/4q2 і 0. Следовательно, при фиксированном q значение
функции f(x,y) максимально, если d = 0, т. е. x = y; случай x = y
разобран выше.
-
10.21.
-
Ясно, что
|
1
a
|
+ |
1
b
|
+ |
1
c
|
= (ha + hb + hc)/2S
|
. Кроме того, 9r Ј ha + hb + hc (задача 10.12)
и ha + hb + hc Ј ma + mb + mc Ј 9R/2 (задача 10.5, б)).
-
10.22.
-
Докажем сначала, что b + c – a < 2bc/a. Пусть 2x = b + c – a,2y = a + c – b и 2z = a + b – c. Требуется доказать, что 2x < 2(x + y)(x + z)/(y + z),
т. е. xy + xz < xy + xz + x2 + yz. Последнее неравенство очевидно.
Так как 2bccos a
= b2 + c2 – a2 = (b + c – a)(b + c + a) – 2bc,
то
|
|
2bccos a
b + c
|
= b + c – a + |
й
л
|
(b + c – a)a
b + c
|
– |
2bc
b + c
|
щ
ы
|
. |
|
Выражение в квадратных скобках отрицательно, так как b + c – a < 2bc/a.
-
10.23.
-
Согласно задаче 12.30
a2 + b2 + c2 = (a + b + c)2 – 2(ab + bc + ac) = 4p2 – 2r2 – 2p2 – 8rR = 2p2 – 2r2 – 8rR
и abc = 4prR.
Таким образом, нужно
доказать неравенство 2p2 – 2r2 – 8rR < 2(1 – 4prR), где p = 1. Это
неравенство очевидно.
-
10.24.
-
Согласно задаче 12.30 ab + bc + ca = r2 + p2 + 4Rr. Кроме
того, 16Rr – 5r2 Ј p2 Ј 4R2 + 4Rr + 3r2 (задача 10.34).
-
10.25.
-
Так как r(ctg a + ctg b) = c = rc(tg a + tg b),
то
|
c2 = rrc |
ж
и
|
2 + |
tg a
tg b
|
+ |
tg b
tg a
|
ц
ш
|
і 4rrc. |
|
-
10.26.
-
Достаточно воспользоваться результатами задач 12.36, а)
и 10.45. Заметим также, что x(1 – x) Ј 1/4, т. е. r/R Ј 1/2.
-
10.27.
-
Так как hc Ј a и hc Ј b, то 4S = 2chc Ј c(a + b). Поэтому 6r(a + b + c) = 12S Ј 4ab + 4S Ј (a + b)2 + c(a + b) = (a + b)(a + b + c).
-
10.28.
-
Так как
(задача 12.21),
то
|
ra
ha
|
= |
ж
и
|
ra
rb
|
+ |
ra
rc
|
ц
ш
|
/2
|
.
Запишем аналогичные равенства для rb/hb и rc/hc и сложим их.
Учитывая, что
, получаем требуемое.
-
10.29.
-
Так как Rr = RS/p = abc/4p (см. задачу 12.1), то приходим
к неравенству 27abc Ј 8p3 = (a + b + c)3.
Так как (a + b + c)2 Ј 3(a2 + b2 + c2) для любых чисел a,b и c,
то p2 Ј 3(a2 + b2 + c2)/4 = ma2 + mb2 + mc2 (см. задачу 12.11, б)).
Остается заметить, что ma2 + mb2 + mc2 Ј 27R2/4
(задача 10.5, а)).
-
10.30.
-
Так как OA = r/sin (A/2), OB = r/sin (B/2)
и OC = r/sin (C/2), а углы РA/2, РB/2 и РC/2
острые, то РA Ј РB Ј РC. Следовательно,
РA Ј 60° и РB Ј 90°, а значит,
sin (A/2) Ј 1/2 и sin (B/2) Ј 1/Ц2.
-
10.31.
-
Если РC і 120°, то сумма расстояний
от любой точки внутри треугольника до его вершин не меньше a + b
(задача 12.21); кроме того, a + b і 6r (задача 12.27).
Если все углы треугольника меньше 120°, то в точке минимума
суммы расстояний до вершин треугольника квадрат этой суммы
равен (a2 + b2 + c2)/2 + 2Ц3S (задача 18.22, б)). Далее,
(a2 + b2 + c2)/2 і 2Ц3S (задача 10.53, б)) и 4Ц3S і 36r2 (задача 10.53, а)).
-
10.32.
-
Пусть a
= cos (A/2), b
= cos (B/2) и g
= cos (C/2).
Согласно задаче 12.17, б) a/ra = a/bg, b/rb = b/ga
и c/rc = g/ab. Поэтому после домножения на abg требуемое
неравенство перепишется в виде 3(a2 + b2 + g2) і 4(b2g2 + g2a2 + a2b2).
Так как a2 = (1 + cos A)/2,b2 = (1 + cos B)/2 и g2 = (1 + cos C)/2, то переходим
к неравенству cos A + cos B + cos C + 2(cos Acos B + cos Bcos C + cos Ccos A) Ј 3. Остается воспользоваться результатами задач 10.36
и 10.43.
-
10.33.
-
а) Сложив равенство 4R + r = ra + rb + rc
(задача 12.24)
с неравенством R – 2r і 0
(задача 10.26), получим
|
5R – r і ra + rb + rc = pr((p – a) – 1 + (p – b) – 1 + (p – c) – 1) = |
|
|
= p(ab + bc + ca – p2)/S = p(2(ab + bc + ca) – a2 – b2 – c2)/4S. |
|
Остается заметить, что 2(ab + bc + ac) – a2 – b2 – c2 і 4Ц3S (задача 10.54).
б) Легко проверить,
что 4R – ra = rb + rc – r = pr/(p – b) + pr/(p – c) – pr/p = (p – a)(p2 – bc)/S.
Остается заметить, что
4(p2–bc) = a2 + b2 + c2 + 2(ab – bc + ca) = 2(ab + bc + ac) – a2 – b2 – c2 + 2(a2 + b2 + c2 – 2bc) і 4Ц3S + 2(a2 + (b – c)2).
-
10.34.
-
Пусть a,b и c- длины сторон треугольника,
F = (a – b)(b – c)(c – a) = A – B, где A = ab2 + bc2 + ca2 и B = a2b + b2c + c2a.
Докажем, что требуемые неравенства можно получить, преобразовав
очевидное неравенство F2 і 0. Пусть s1 = a + b + c = 2p,s2 = ab + bc + ca = r2 + p2 + 4rR и s3 = abc = 4prR (см. задачу 12.30).
Можно проверить, что F2 = s12s22 – 4s23 – 4s13s3 + 18s1s2s3 – 27s32. В самом деле, (s1s2)2 – F2 = (A + B + 3abc)2-(A – B)2 = 4AB + 6(A + B)s3 + 9s32 = 4(a3b3 + …) + 4(a4bc + …) + 6(A + B)s3 + 21s32. Ясно также, что
4s23 = 4(a3b3 + …) + 12(A + B)s3 + 24s32,4s13s3 = 4(a4bc + …) + 12(A + B)s3 + 24s32
и 18s1s2s3 = 18(A + B)s3 + 54s32.
Выразив s1,s2 и s3 через p,r и R, получим
|
F2 = – 4r2[(p2 – 2R2 – 10Rr + r2)2 – 4R(R – 2r)3] і 0. |
|
Следовательно, получаем
|
p2 і 2R2 + 10Rr – r2 – 2(R – 2r) |
Ц
|
R(R – 2r)
|
= |
|
|
= [(R – 2r) – |
Ц
|
R(R – 2r)
|
]2 + 16Rr – 5r2 і
16Rr – 5r2
|
|
и
|
p2 Ј 2R2 + 10Rr + r2 + 2(R – 2r) |
Ц
|
R(R – 2r)
|
= |
|
|
= 4R2 + 4Rr + 3r2 – [(R – 2r) – |
Ц
|
R(R – 2r)
|
]2 Ј 4R2 + 4Rr + 3r2. |
|
-
10.35.
-
Так как ra + rb + rc = 4R + r и rarb + rbrc + rcra = p2
(задачи 10.24 и 10.25), то ra2 + rb2 + rc2 = (4R + r)2 – 2p2. Согласно
задаче 10.34 p2 Ј 4R2 + 4Rr + 3r2, поэтому
ra2 + rb2 + rc2 і 8R2 – 5r2. Остается заметить, что r Ј R/2
(задача 10.26).
-
10.36.
-
а) Согласно задаче 12.38
cos a + cos b + cos g
= (R + r)/R. Кроме того, r Ј R/2
(задача 10.26).
б) Следует из а) (см. замечание).
-
10.37.
-
а) Ясно, что sin a + sin b + sin g
= p/R. Кроме того,
p Ј 3Ц3 R/2 (задача 10.29).
б) Следует из а) (см. замечание).
-
10.38.
-
а) Согласно задаче 12.44, а)
ctg a + ctg b + ctg g
= (a2 + b2 + c2)/4S. Кроме того,
a2 + b2 + c2 і 4Ц3S (задача 10.53, б)).
б) Следует из а) (см. замечание).
-
10.39.
-
а) Согласно задаче 12.44, а)
ctg (a/2) + ctg (b/2) + ctg (g/2) = p/r. Кроме того,
p і 3Ц3r (задача 10.53, а)).
б) Следует из а) (см. замечание). Для тупоугольного треугольника
tg a + tg b + tg g < 0; см., например, задачу 12.46.
-
10.40.
-
а) Согласно задаче 12.36, а)
sin (a/2)sin (b/2)sin (g/2) = r/4R. Кроме того,
r Ј R/2 (задача 10.26).
б) Для остроугольного треугольника следует из а) (см. замечание).
Для тупоугольного треугольника cos acos bcos g < 0.
-
10.41.
-
а) Так как sin x = 2sin (x/2)cos (x/2), то, используя
результаты задач 12.36, а) и 12.36, в), получаем
sin asin bsin g
= pr/2R2. Кроме того, p Ј 3Ц3R/2
(задача 10.29) и r Ј R/2 (задача 10.26).
б) Следует из а) (см. замечание).
-
10.42.
-
Согласно задаче 12.39, б)
cos 2a + cos 2b + cos 2g
= 1 – 2cos acos bcos g. Остается
заметить, что cos acos bcos g Ј 1/8 (задача 10.40, б)),
а для тупоугольного треугольника cos acos bcos g < 0.
-
10.43.
-
Ясно, что 2(cos acos b + cos bcos g + cos gcos a) = (cos a + cos b + cos g)2 – cos 2a – cos 2b – cos 2g. Остается заметить, что cos a + cos b + cos g Ј 3/2
(задача 10.36, а)) и cos 2a + cos 2b + cos 2g і 3/4
(задача 10.42).
-
10.44.
-
Пусть продолжения биссектрис остроугольного
треугольника ABC с углами a,b и g пересекают описанную
окружность в точках A1,B1 и C1. Тогда SABC = R2(sin 2a + sin 2b + sin 2g)/2 и SA1B1C1 = R2(sin (a + b) + sin (b + g) + sin (g + a))/2. Остается воспользоваться результатами
задач 12.72 и 10.26.
-
10.45.
-
Ясно, что 2sin (b/2)sin (g/2) = cos ((b – g)/2) – cos ((b + g)/2) Ј 1 – sin (a/2).
-
10.46.
-
Опустим из вершин A и B перпендикуляры AA1
и BB1 на биссектрису угла ACB. Тогда AB і AA1 + BB1 = bsin (g/2) + asin (g/2).
-
10.47.
-
Согласно задаче 12.32 tg (a/2)tg (b/2) = (a + b – c)/(a + b + c). А так как a + b < 3c, то a + b – c < (a + b + c)/2.
-
10.48.
-
Так как p – 2a > 0, p – 2b > 0, p – 2g > 0
и (p – 2a) + (p – 2b) + (p – 2g) = p, существует треугольник
с углами p – 2a, p – 2b, p – 2g. Длины сторон, противолежащих
углам p – 2a, p – 2b, p – 2g, пропорциональны числам
sin (p – 2a) = sin 2a, sin 2b, sin 2g. Поскольку p – 2a > p – 2b > p – 2g и против большего угла лежит бóльшая сторона,
то sin 2a > sin 2b > sin 2g.
-
10.49.
-
Заметим сначала, что cos 2g – cos (p – a – b) = cos 2acos 2b – sin 2asin 2b.
Поэтому cos 2a + cos 2b – cos 2g
= cos 2a + cos 2b – cos 2acos 2b + sin 2asin 2b. Так как
| acos j + bsin j Ј |
Ц
|
a2 + b2
|
|
(см.
приложение к гл. 9), то
| (1 – cos 2b)cos 2a + sin 2bsin 2a + cos 2b Ј |
Ц
|
(1 – cos 2b)2 + sin 22b
|
+ cos 2b
= 2|sin b| + 1 – 2sin 2b
|
. Остается заметить, что наибольшее значение
квадратного трехчлена 2t + 1 – 2t2 достигается в точке t = 1/2
и равно 3/2. Максимальное значение соответствует
углам a
= b
= 30°, g
= 120°.
-
10.50.
-
Так как AB < CB, AX < CX и SABX = SBCX,
то sin XAB > sin XCB. Учитывая, что угол XCB острый, получаем
требуемое.
-
10.51.
-
Если углы треугольника ABC равны a,b и g,
то углы треугольника A1B1C1 равны (b + g)/2, (g + a)/2
и (a + b)/2.
-
10.52.
-
Пусть M- точка пересечения медиан AA1,BB1
и CC1. Достроив треугольник AMB до параллелограмма AMBN,
получим РBMC1 = am и РAMC1 = bm. Легко проверить,
что РC1CB < g/2 и РB1BC < b/2. Следовательно,
am = РC1CB + РB1BC < (b + g)/2 < b.
Аналогично gm = РA1AB + РB1BA > (a + b)/2 > b.
Предположим сначала, что треугольник ABC остроугольный. Тогда
точка H пересечения высот лежит внутри треугольника AMC1.
Следовательно, РAMB < РAHB, т. е. p – gm < p – g,
и РCMB > РCHB, т. е. p – am < p – a. Предположим
теперь, что угол a тупой. Тогда угол CC1B тоже тупой, а значит,
угол am острый, т. е. am < a. Опустим из точки M
перпендикуляр MX на BC. Тогда gm > РXMB > 180° – РHAB > g.
Так как a > am, то a + (p – am) > p, т. е. точка M лежит
внутри описанной окружности треугольника AB1C1. Следовательно,
g
= РAB1C1 < РAMC1 = bm. Аналогично a
= РCB1A1 > РCMA1 = bm, так как g + (p – gm) < p.
-
10.53.
-
а) Ясно, что S2/p = (p – a)(p – b)(p – c) Ј ((p – a + p – b + p – c)/3)3 = p3/27.
Поэтому pr = S Ј p2/3Ц3,
т. е. r Ј p/3Ц3.
Домножив последнее неравенство на r, получим требуемое.
б) Так как (a + b + c)2 Ј 3(a2 + b2 + c2), то S Ј p2/3Ц3 = (a + b + c)2/12Ц3 Ј (a2 + b2 + c2)/4Ц3.
-
10.54.
-
Пусть x = p – a, y = p – b, z = p – c. Тогда (a2 – (b – c)2) + (b2 – (a – c)2) + (c2 – (a – b)2) = 4(p – b)(p – c) + 4(p – a)(p – c) + 4(p – a)(p – b) = 4(yz + zx + xy)
и
|
4Ц3S = 4 |
Ц
|
3p(p – a)(p – b)(p – c)
|
= 4 |
Ц
|
3(x + y + z)xyz
|
. |
|
Итак, нужно доказать неравенство
| xy + yz + zx і |
Ц
|
3(x + y + z)xyz
|
|
. После возведения в квадрат и сокращения получаем
|
x2y2 + y2z2 + z2x2 і x2yz + y2xz + z2xy. |
|
Складывая неравенства x2yz Ј x2(y2 + z2)/2,y2xz Ј y2(x2 + z2)/2 и z2xy Ј z2(x2 + y2)/2, получаем
требуемое.
-
10.55.
-
а) Перемножив три равенства вида S = (absin g)/2,
получим S3 = ((abc)2sin gsin bsin a)/8. Остается
воспользоваться результатом задачи 10.41.
б) Так как (hahbhc)2 = (2S)6/(abc)2
и (abc)2 і (4/Ц3)3S3, то (hahbhc)2 Ј (2S)6(Ц3/4)3/S3 = (Ц3S)3.
Так как (rarbrc)2 = S4/r2 (задача 12.18, в)
и r2(Ц3)3 Ј S (задача 10.53, а)),
то (rarbrc)2 і (Ц3S)3.
-
10.56.
-
Пусть p = BA1/BC, q = CB1/CA и r = AC1/AC.
Тогда SA1B1C1/SABC = 1 – p(1 – r) – q(1 – p) – r(1 – q) = 1 – (p + q + r) + (pq + qr + rp).
По теореме Чевы (задача 5.77)
pqr = (1 – p)(1 – q)(1 – r),
т. е. 2pqr = 1 – (p + q + r) + (pq + qr + rp);
кроме того,
(pqr)2 = p(1 – p)q(1 – q)r(1 – r) Ј (1/4)3.
Следовательно,
| SA1B1C1/SABC = 2pqr Ј |
1
4
|
|
.
-
10.57.
-
Можно считать, что площадь треугольника ABC равна 1.
Тогда a + b + c = 1 – u, поэтому данное неравенство перепишется
в виде u2 і 4abc. Пусть x = BA1/BC, y = CB1/CA и z = AC1/AB.
Тогда u = 1 – (x + y + z) + xy + yz + zx и abc = xyz(1 – x)(1 – y)(1 – z) = v(u – v),
где v = xyz. Поэтому мы переходим к неравенству u2 і 4v(u – v),
т. е. (u – 2v)2 і 0. Последнее неравенство очевидно.
-
10.58.
-
а) Пусть x = BA1/BC, y = CB1/CA и z = AC1/AB. Можно
считать, что площадь треугольника ABC равна 1. Тогда
SAB1C1 = z(1 – y), SA1BC1 = x(1 – z) и SA1B1C = y(1 – x). Так
как x(1 – x) Ј 1/4, y(1 – y) Ј 1/4 и z(1 – z) Ј 1/4, то произведение
чисел SAB1C1, SA1BC1 и SA1B1C
не превосходит (1/4)3, а значит, одно из них не превосходит 1/4.
б) Пусть для определенности x і 1/2.
Если y Ј 1/2,
то при гомотетии с центром C и коэффициентом 2 точки A1 и B1 переходят
во внутренние точки сторон BC и AC, а значит,
SA1B1C Ј SA1B1C1.
Поэтому можно считать, что y і 1/2 и аналогично z і 1/2.
Пусть x = (1 + a)/2, y = (1 + b)/2 и z = (1 + g)/2.
Тогда SAB1C1 = (1 + g – b – bg)/4,SA1BC1 = (1 + a – g – ag)/4 и SA1B1C = (1 + b – a–ab)/4,
а значит, SA1B1C1 = (1 + ab + bg +
ag)/4 и SAB1C1 + SA1BC1 + SA1B1C Ј 3/4.
-
10.59.
-
Достаточно доказать, что если AC < BC, то РABC < РBAC. Так как AC < BC, то на стороне BC можно выбрать
точку A1 так, что A1C = AC. Тогда РBAC > РA1AC = РAA1C > РABC.
-
10.60.
-
Пусть A1- середина стороны BC.
Если AA1 < BC/2 = BA1 = A1C,
то РBAA1 > РABA1
и РCAA1 > РACA1,
поэтому РA = РBAA1 + РCAA1 > РB + РC,
т. е. РA > 90°.
Аналогично, если AA1 > BC/2, то РA < 90°.
-
10.61.
-
Если мы фиксируем две стороны треугольника, то чем
больше будет угол между ними, тем больше будет третья сторона. Поэтому
из неравенства РA > РA1 следует, что BD > B1D1,
т. е. РC > РC1. Предположим теперь, что РB і РB1. Тогда AC і A1C1, т. е. РD > РD1.
Поэтому 360° = РA + РB + РC + РD > РA1 + РB1 + РC1 + РD1 = 360°. Получено
противоречие; следовательно, РB < РB1 и РD < РD1.
-
10.62.
-
Пусть точка B1 симметрична B относительно
точки M. Так как высота, опущенная из точки M на сторону BC,
равна половине AH, т. е. половине BM, то РMBC = 30°.
Поскольку AH- наибольшая из высот, то BC- наименьшая
из сторон. Поэтому AB1 = BC Ј AB, т. е. РABB1 Ј РAB1B = РMBC = 30°. Следовательно, РABC = РABB1 + РMBC Ј 30° + 30° = 60°.
-
10.63.
-
Предположим сначала, что РA > РD.
Тогда BE > EC и РEBA < РECD.
Так как в треугольнике EBC
сторона BE больше стороны EC, то РEBC < РECB.
Поэтому РB = РABE + РEBC < РECD + РECB = РC,
что противоречит условию задачи.
Значит, РA = РB = РC = РD.
Аналогично предположение РB > РE
приводит к неравенству РC < РD. Поэтому РB = РC = РD = РE.
-
10.64.
-
Будем проводить доказательство сразу для общего случая.
Пусть прямая MN пересекает стороны многоугольника в точках M1
и N1. Ясно, что MN Ј M1N1. Пусть точка M1 лежит
на стороне AB, а точка N1- на PQ. Так как РAM1N1 + РBM1N1 = 180°, то один из этих углов
не меньше 90°. Пусть для определенности РAM1N1 і 90°. Тогда AN1 і M1N1, так как против
большего угла лежит бóльшая сторона. Аналогично доказывается, что
либо AN1 Ј AP, либо AN1 Ј AQ. Следовательно, длина
отрезка MN не превосходит длины отрезка с концами в вершинах
многоугольника.
-
10.65.
-
Отрезок можно продолжить до пересечения с границей сектора, так как
при этом его длина только увеличится. Поэтому можно считать, что
точки M и N лежат на границе сектора. Возможны три случая.
1. Точки M и N лежат на дуге окружности. Тогда MN = 2Rsin (MON/2) Ј 2Rsin (AOB/2) = AB, так как РMON/2 Ј РAOB/2 Ј 90°.
2. Точки M и N лежат на отрезках AO и BO. Тогда MN
не превосходит наибольшей стороны треугольника AOB.
3. Одна из точек M и N лежит на дуге окружности, а другая-
на отрезке AO или BO. Пусть для определенности M лежит на AO,
а N- на дуге окружности. Тогда MN не превосходит наибольшей
стороны треугольника ANO. Остается заметить, что AO = NO = R и AN Ј AB.
-
10.66.
-
Если данный отрезок не имеет общих точек с окружностью, то с помощью
гомотетии с центром A (и коэффициентом больше 1) его можно
перевести в отрезок, имеющий общую точку X с дугой AB
и лежащий в нашей области. Проведем через точку X
касательную DE к окружности (точки D и E лежат
на отрезках AB и AC). Тогда отрезки AD и AE
меньше AB и DE <
(DE + AD + AE)/2 = AB, т. е. все стороны
треугольника ADE меньше AB. Так как наш отрезок лежит
внутри треугольника ADE (или на его стороне DE), то его
длина не превосходит AB.
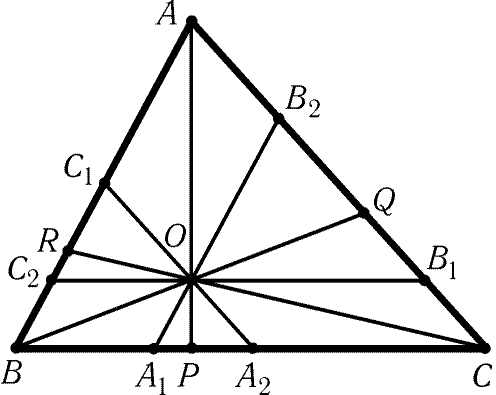
Рис. 10.1
10.67. Предположим сначала, что центр O окружности лежит
внутри данного пятиугольника A1A2A3A4A5. Рассмотрим углы
A1OA2, A2OA3,…, A5OA1. В сумме эти пять углов дают 2p,
поэтому один из них, например A1OA2, не превосходит 2p/5. Тогда
отрезок A1A2 можно поместить в сектор OBC, где РBOC = 2p/5 и точки B и C расположены на окружности.
В треугольнике OBC наибольшей стороной является BC,
поэтому A1A2 Ј BC.
Если точка O не принадлежит данному пятиугольнику, то углы A1OA2,…, A5OA1 дают в объединении угол меньше p, причем каждая
точка этого угла покрыта ими дважды. Поэтому в сумме эти пять углов
дают меньше 2p, т. е. один из них меньше 2p/5. Дальнейшее
доказательство аналогично предыдущему случаю.
Если точка O лежит на стороне пятиугольника, то один
из рассматриваемых углов не больше p/4, а если она является его
вершиной, то один из них не больше p/3. Ясно,
что p/4 < p/3 < 2p/5.
-
10.68.
-
Возьмем на сторонах BC, CA, AB точки A1 и A2,
B1 и B2, C1 и C2 так, что B1C2||BC, C1A2||CA,A1B2||AB (рис. 10.1). В треугольниках A1A2O, B1B2O, C1C2O
наибольшими сторонами являются A1A2, B1O, C2O соответственно.
Поэтому OP < A1A2, OQ < B1O, OR Ј C2O, т. е. OP + OQ + OR < A1A2 + B1O + C2O = A1A2 + CA2 + BA1 = BC.
-
10.69.
-
Так как c2 = a2 + b2, то cn = (a2 + b2)cn – 2 = a2cn – 2 + b2cn – 2 > an + bn.
-
10.70.
-
Высота любого треугольника больше 2r. Кроме того,
в прямоугольном треугольнике 2r = a + b – c (задача 5.16).
-
10.71.
-
Так как ch = 2S = r(a + b + c) и
,
то
, где
. Так как 0 < 2ab/(a2 + b2) Ј 1,
то 1 < x Ј Ц2. Следовательно, 2/5 < 1/(1 + Ц2) Ј r/h < 1/2.
-
10.72.
-
Ясно, что
и c2 = a2 + b2 і 2ab.
Поэтому
|
|
c2
r2
|
= |
(a + b + c)2c2
a2b2
|
і |
a2b2
|
= 4(1 + Ц2)2. |
|
-
10.73.
-
Согласно задаче 12.11,
а) ma2 + mb2 = (4c2 + a2 + b2)/4 = 5c2/4.
Кроме того, 5c2/4 і 5(1 + Ц2)2r2 = (15 + 10Ц2)r2 > 29r2
(см. задачу 10.72).
-
10.74.
-
Пусть O- центр описанной окружности,
A1,B1,C1- середины сторон BC, CA, AB соответственно.
Тогда ma = AA1 Ј AO + OA1 = R + OA1. Аналогично mb Ј R + OB1
и mc Ј R + OC1. Следовательно,
|
|
ma
ha
|
+ |
mb
hb
|
+ |
mc
hc
|
Ј R |
ж
и
|
1
ha
|
+ |
1
hb
|
+ |
1
hc
|
ц
ш
|
+ |
OA1
ha
|
+ |
OB1
hb
|
+ |
OC1
hc
|
. |
|
Остается воспользоваться результатом задачи 12.22 и решением
задачи 4.46.
-
10.75.
-
Согласно задаче 4.47
|
1
b
|
+ |
1
c
|
= |
2cos (a/2)
la
|
і |
Ц2
la
|
|
. Складывая три
аналогичных неравенства, получаем требуемое.
-
10.76.
-
Обозначим точку пересечения медиан через M, а центр
описанной окружности через O. Если треугольник ABC не тупоугольный,
то точка O лежит внутри его (или на его стороне); для определенности
будем считать, что она лежит внутри треугольника AMB.
Тогда AO + BO Ј AM + BM, т. е. 2R Ј 2ma/3 + 2mb/3
или ma + mb і 3R. Остается заметить, что так как угол COC1
(C1- середина AB) тупой, то CC1 і CO, т. е. mc і R.
Равенство достигается только для вырожденного треугольника.
-
10.77.
-
В любом треугольнике hb Ј lb Ј mb
(см. задачу 2.68), поэтому ha = lb і hb
и mc = lb Ј mb. Следовательно, a Ј b и b Ј c (см.
задачу 10.1), т. е. c - наибольшая сторона,
а g- наибольший угол.
Из равенства ha = mc следует, что g Ј 60° (см.
задачу 10.62). Так как наибольший угол g треугольника ABC
не превосходит 60°, все углы треугольника 60°.
-
10.78.
-
Согласно задаче 1.60 отношение
периметров треугольников A1B1C1 и ABC равно r/R. Кроме
того, r Ј R/2 (задача 10.26).
Замечание.
Используя результат задачи 12.72, легко проверить,
что SA1B1C1/SABC = r1/2R1 Ј 1/4.
-
10.79.
-
Пусть AA1 и BB1 - биссектрисы треугольников OAH и OBH. Согласно
задаче 2.1 они являются биссектрисами углов A и B, т.е. центр вписанной
окружности - точка пересечения прямых AA1 и BB1. Из неравенства
AC > BC следует, что AH > BH. Поэтому
|
A1H/A1O = AH/AO > BH/BO = B1H/B1O, |
|
т. е. точки на прямой OH расположены в таком порядке: O, A1, B1, H.
Точка O лежит внутри треугольника ABH, поэтому точка пересечения прямых
AA1 и BB1 лежит внутри треугольника BOH.
-
10.80.
-
Пусть 90° і a і b і g.
Тогда CH- наибольшая высота. Центры вписанной и описанной
окружностей обозначим через I и O, точки касания вписанной
окружности со сторонами BC,CA,AB- через K,L,M соответственно
(рис. 10.2).
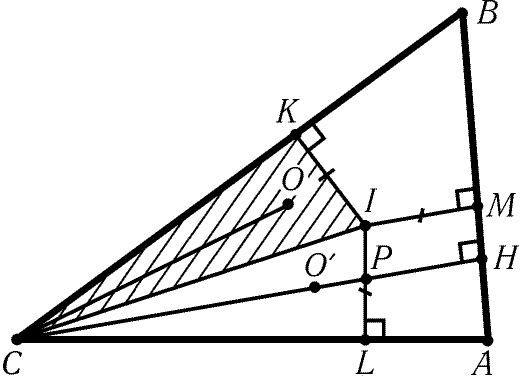
Рис. 10.2
Докажем сначала, что точка O лежит внутри треугольника KCI.
Для этого достаточно доказать, что CK і KB и РBCO Ј BCI.
Ясно, что CK = rctg (g/2) і rctg (b/2) = KB и 2РBCO = 180° – РBOC = 180° – 2a Ј 180° – a – b
= g
= 2РBCI. Так как РBCO = 90° – a
= РACH, при симметрии относительно CI
прямая CO переходит в прямую CH. Пусть Oў- образ точки O
при этой симметрии, P- точка пересечения CH и IL.
Тогда CP і COў = CO = R. Остается доказать, что PH і IM = r. Это
следует из того, что РMIL = 180° – a і 90°.
10.81. Пусть B2C2- проекция отрезка B1C1
на сторону BC. Тогда B1C1 і B2C2 = BC – BC1cos b – CB1cos g.
Аналогично A1C1 і AC – AC1cos a – CA1cos g
и A1B1 і AB – AB1cos a – BA1cos b.
Домножим эти неравенства
на cos a, cos b и cos g соответственно и сложим их.
Получим B1C1cos a + C1A1cos b + A1B1cos g і acos a + bcos b + ccos g – (acos bcos g + bcos acos g + ccos acos b).
Так как c = acos b + bcos a,
то ccos g = acos bcos g + bcos acos g.
Записав три аналогичных
неравенства и сложив их, получим acos bcos g + bcos acos g + ccos acos b
= (acos a + bcos b + ccos g)/2.
-
10.82.
-
Так как cos 2a + cos 2b + cos 2g + 2cos acos bcos g
= 1 (задача 12.39, б)), то треугольник ABC
остроугольный тогда и только тогда,
когда cos 2a + cos 2b + cos 2g < 1, т. е.
sin 2a + sin 2b + sin 2g > 2. Домножая обе части последнего
неравенства на 4R2, получаем требуемое.
-
10.83.
-
Достаточно заметить, что p2 – (2R + r)2 = 4R2cos acos bcos g (см. задачу 12.41, б)).
-
10.84.
-
Пусть РA Ј РB Ј РC. Если
треугольник ABC не остроугольный, то CC1 < AC < AA1 для любых
точек A1 и C1 на сторонах BC и AB. Докажем теперь, что
для остроугольного треугольника можно выбрать точки A1,B1 и C1,
обладающие требуемым свойством. Для этого достаточно проверить, что
существует число x, удовлетворяющее следующим неравенствам:
,
и
. Остается заметить,
что
,
и ha < b.
-
10.85.
-
Пусть РA Ј РB Ј РC. Предположим
сначала, что треугольник ABC остроугольный. При повороте прямой l,
в исходном положении параллельной AB, длина проекции треугольника
на l будет сначала монотонно изменяться от c до hb, затем
от hb до a, от a до hc, от hc до b, от b до ha
и, наконец, от ha до c. Так как hb < a, то существует такое
число x, что hb < x < a. Легко проверить, что отрезок длиной x
встречается на любом из первых четырех интервалов монотонности.
Предположим теперь, что треугольник ABC не остроугольный.
При повороте прямой l, в исходном положении параллельной AB, длина
проекции треугольника на l монотонно убывает сначала от c до hb,
затем
от hb до hc; после этого она монотонно возрастает сначала
от hc до ha, а затем
от ha до c.
Всего получается два
интервала монотонности.
-
10.86.
-
Пусть точки M и N лежат на сторонах AB и AC
соответственно. Проведем через вершину C прямую, параллельную
стороне AB. Пусть N1- точка пересечения этой прямой
и прямой MN. Тогда N1O : MO = 2, но NO Ј N1O,
поэтому NO : MO Ј 2.
-
10.87.
-
Окружность S, вписанная в треугольник ABC, лежит
внутри треугольника AўBўCў. Проведя к этой окружности касательные,
параллельные сторонам треугольника AўBўCў, можно получить
треугольник AўўBўўCўў, подобный треугольнику AўBўCў,
для которого S является вписанной окружностью.
Поэтому rABC = rAўўBўўCўў < rAўBўCў.
-
10.88.
-
Биссектриса lc разбивает треугольник ABC на два
треугольника, удвоенные площади которых равны alcsin (g/2)
и blcsin (g/2). Поэтому aha = 2S = lc(a + b)sin (g/2). Из условия
задачи следует, что a/(a + b) Ј 1/2 Ј sin (g/2).
-
10.89.
-
Ясно, что ctg A + ctg B = c/hc і c/mc. Пусть M
- точка пересечения медиан, N- середина отрезка AB. Так
как треугольник AMB прямоугольный, MN = AB/2. Следовательно,
c = 2MN = 2mc/3.
-
10.90.
-
Так как BN · BA = BM2 и BM < BA, то BN < BM,
а значит, AN > CN.
-
10.91.
-
Проведем через точку B перпендикуляр к стороне AB.
Пусть F- точка пересечения этого перпендикуляра с продолжением
стороны AC (рис. 10.3). Докажем, что биссектриса AD, медиана BM
и высота CH пересекаются в одной точке тогда и только тогда,
когда AB = CF. В самом деле, пусть L- точка пересечения BM
и CH. Биссектриса AD проходит через точку L тогда и только тогда,
когда BA : AM = BL : LM, но BL : LM = FC : CM = FC : AM.
Если на стороне AF некоторого прямоугольного треугольника ABF
(РABF = 90°) отложить отрезок CF = AB, то углы BAC
и ABC будут острыми. Остается выяснить, в каких случаях угол ACB
будет острым. Опустим из точки B перпендикуляр BP на сторону AF.
Угол ACB острый, если FP > FC = AB, т. е. BFsin A > BFctg A.
Следовательно, 1 – cos 2A = sin 2A > cos A, т. е. cos A < (Ц5 – 1)/2. В итоге получаем, что
|
90° > РA > arccos (( |
Ц
|
5 – 1
|
)/2) » 51°50ў. |
|
-
10.92.
-
Так как против большей стороны лежит больший угол,
то (a – b)(a – b) і 0, (b – c)(b – g) і 0 и (a – c)(a – g) і 0.
Складывая эти неравенства, получаем
|
2(aa + bb + cg) і a(b + g) + b(a + g) + c(a + b) = (a + b + c)p – aa – bb-cg, |
|
т. е.
p/3 Ј (aa + bb + cg)/(a + b + c).
Из неравенства треугольника следует, что
|
a(b + c – a) + b(a + c – b) + g(a + b – c) > 0, |
|
т. е. a(b + g – a) + b(a + g – b) + c(a + b – g) > 0. Так
как a + b + g
= p, то a(p – 2a) + b(p – 2b) + c(p – 2g) > 0,
т. е. (aa + bb + cg)/(a + b + c) < p/2.
-
10.93.
-
Возьмем на лучах OB и OC такие точки C1 и B1,
что OC1 = OC и OB1 = OB. Пусть B2 и C2- проекции
точек B1 и C1 на прямую, перпендикулярную AO. Тогда BOsin AOC + COsin AOB = B2C2 Ј BC. Сложив три аналогичных неравенства,
получим требуемое. Легко проверить также, что условие B1C1^AO,C1A1^BO и A1B1^CO эквивалентно тому, что O-
точка пересечения биссектрис.
-
10.94.
-
Так как РCBD = РC/2 и РB і РA, то РABD = РB + РCBD і (РA + РB + РC)/2 = 90°.
-
10.95.
-
По свойству биссектрисы BM : MA = BC : CA
и BK : KC = BA : AC. Поэтому BM : MA = BK : KC,
т. е.
|
|
AB
AM
|
= 1 + |
BM
MA
|
< 1 + |
BK
KC
|
= |
CB
CK
|
. |
|
Следовательно, точка M более удалена от прямой AC, чем точка K,
т. е. РAKM > РKAC = РKAM и РKMC < РMCA = РMCK. Поэтому AM > MK и MK > KC (см. задачу 10.59).
-
10.96.
-
Предположим, что все данные отношения меньше 2.
Тогда SABO + SAOC < 2SXBO + 2SXOC = 2SOBC,SABO + SOBC < 2SAOC и SAOC + SOBC < 2SABO. Сложив эти
неравенства, приходим к противоречию. Аналогично доказывается, что одно
из данных соотношений не больше 2.
-
10.97.
-
Обозначим радиусы окружностей S,S1 и S2
через r,r1 и r2. Пусть треугольники AB1C1 и A2BC2 подобны
треугольнику ABC, причем коэффициенты подобия равны r1/r и r2/r
соответственно. Окружности S1 и S2 являются вписанными
для треугольников AB1C1 и A2BC2. Следовательно, эти треугольники
пересекаются, так как иначе окружности S1 и S2 не имели бы общих
точек. Поэтому AB1 + A2B > AB, т. е. r1 + r2 > r.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:45.

 Глава 10. Задачи для самостоятельного решения |
Глава 10. Задачи для самостоятельного решения | 

 Глава 10. Задачи для самостоятельного решения |
Глава 10. Задачи для самостоятельного решения | 

