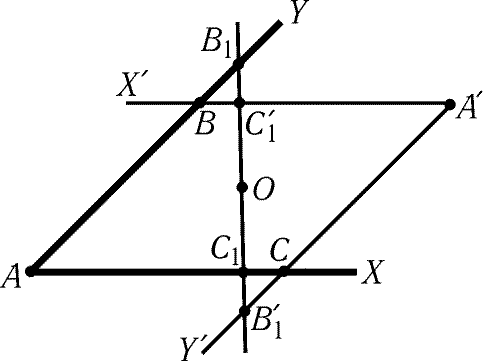| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
11.1.
-
По теореме косинусов a2 = b2 + c2 – 2bccos a
= (b – c)2 + 2bc(1 – cos a) = (b – c)2 + 4S(1 – cos a)/sin a. Так как второе слагаемое постоянно,
то a минимально, если b = c.
-
11.2.
-
Пусть вневписанная окружность касается сторон AB и AC в точках K
и L. Так как AK = AL = p, то вневписанная окружность Sa фиксирована.
Радиус r вписанной окружности максимален, когда она касается
окружности Sa, т. е. треугольник ABC равнобедренный. Ясно
также, что S = pr.
-
11.3.
-
Согласно задаче 10.53, а) S Ј p2/3Ц3, причем равенство
достигается только для правильного треугольника.
-
11.4.
-
По теореме косинусов b2 + c2 = a2 + 2bccos a. Так как 2bc Ј b2 + c2
и cos a > 0, то b2 + c2 Ј a2 + (b2 + c2)cos a, т. е.
b2 + c2 Ј a2/(1 – cos a). Равенство достигается, если b = c.
-
11.5.
-
Пусть O - центр окружности радиуса R; A, B и C -
вершины треугольника;
,
,
. Тогда AB2 + BC2 + CA2 = |a – b|2 + |b – c|2 + |c – a|2 = 2(|a|2 + |b|2 + |c|2)-2(a, b) – 2(b, c) – 2(c, a).
Так как |a + b + c|2 = |a|2 + |b|2 + |c|2 + 2(a, b) + 2(b, c) + 2(c, a),
то AB2 + BC2 + CA2 = 3(|a|2 + |b|2 + |c|2) – |a + b + c|2 Ј 3(|a|2 + |b|2 + |c|2) = 9R2,
причем равенство достигается, только если a + b + c = 0.
Это равенство означает, что треугольник ABC правильный.
-
11.6.
-
Обозначим длину высоты, опущенной на сторону BC, через h.
Так как DAMN ~ DABC, то MN/BC = (h – 2r)/h,
т. е.
. Поскольку r = S/p = ah/2p,
то MN = a(1 – a/p). Максимум выражения a(1 – a/p) = a(p – a)/p
достигается при a = p/2; он равен p/4. Остается заметить, что
существует треугольник периметра 2p со стороной a = p/2 (положим
b = c = 3p/4).
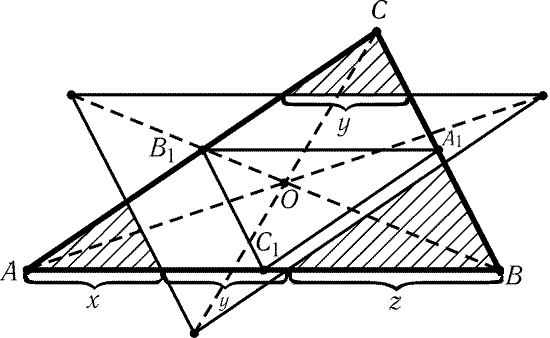
Рис. 11.1
11.7.
Пусть O - центр симметрии многоугольника M, расположенного
внутри треугольника T, S(T) - образ треугольника T
при симметрии относительно точки O. Тогда M лежит и в T, и в S(T).
Поэтому среди всех центрально симметричных многоугольников с данным
центром симметрии, лежащих в T, наибольшую площадь имеет
пересечение T и S(T). Точка O лежит внутри треугольника T,
так как пересечением T и S(T) является выпуклый многоугольник,
а выпуклый многоугольник всегда содержит свой центр симметрии.
Пусть A1, B1 и C1 - середины сторон BC, CA и AB
треугольника T = ABC. Предположим сначала, что точка O лежит
внутри треугольника A1B1C1. Тогда пересечением T и S(T)
является шестиугольник (рис. 11.1). Пусть сторона AB делится
сторонами треугольника S(T) в отношении x : y : z,
где x + y + z = 1. Тогда отношение суммы площадей заштрихованных
треугольников к площади треугольника ABC равно x2 + y2 + z2;
нужно минимизировать это выражение. Так как 1 = (x + y + z)2 = 3(x2 + y2 + z2) – (x – y)2 – (y – z)2 – (z – x)2, то x2 + y2 + z2 і 1/3,
причем равенство достигается только при x = y = z;
последнее равенство означает, что O - точка пересечения
медиан треугольника ABC.
Рассмотрим теперь другой случай: точка O лежит внутри одного
из треугольников AB1C1, A1BC1, A1B1C, например внутри
DAB1C1. В этом случае пересечением T и S(T)
является параллелограмм, причем если мы заменим точку O точкой
пересечения прямых AO и B1C1, то площадь этого параллелограмма
может только увеличиться. Если же точка O лежит на стороне B1C1,
то этот случай уже фактически был нами рассмотрен (нужно положить
x = 0).
Искомым многоугольником является шестиугольник с вершинами в точках,
делящих стороны треугольника на три равные части. Его площадь равна
2/3 площади треугольника.
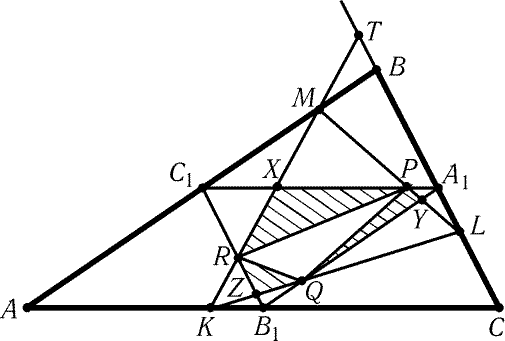
Рис. 11.2
11.8.
Обозначим точку пересечения прямых KM и BC через T, а точки
пересечения сторон треугольников A1B1C1 и KLM так, как
показано на рис. 11.2. Тогда TL : RZ = KL : KZ = LC : ZB1.
Так как TL і BA1 = A1C і LC, то RZ і ZB1, т. е.
SRZQ і SZB1Q. Аналогично SQYP і SYA1P
и SPXR і SXC1R. Складывая все эти неравенства и неравенство
SPQR > 0, получаем, что площадь шестиугольника PXRZQY не меньше
площади оставшейся части треугольника A1B1C1, т. е. его
площадь не меньше SA1B1C1/2 = 1/8. Равенство достигается, например,
если точка K совпадает с B1, а точка M - с B.
11.9.
Так как площадь правильного треугольника со стороной a равна
a2 Ц3/4, сторона правильного треугольника площадью 1
равна 2/ 4Ц3, а его высота 4Ц3. Докажем, что
из полосы шириной меньше 4Ц3 нельзя вырезать правильный
треугольник площадью 1. Пусть правильный треугольник ABC лежит внутри
полосы шириной меньше 4Ц3. Пусть для определенности
проекция вершины B на границу полосы лежит между проекциями
вершин A и C. Тогда прямая, проведенная через точку B
перпендикулярно границе полосы, пересекает отрезок AC в некоторой
точке M. Высота треугольника ABC не превосходит BM, а BM
не больше ширины полосы, поэтому высота треугольника ABC
меньше 4Ц3, т. е. его площадь меньше 1.
Остается доказать, что из полосы шириной 4Ц3 можно вырезать
любой треугольник площадью 1. Докажем, что у любого треугольника
площадью 1 есть высота,
не превосходящая 4Ц3. Для этого
достаточно доказать, что у него есть сторона не меньше 2/ 4Ц3.
Предположим, что все стороны треугольника ABC меньше 2/ 4Ц3.
Пусть a - наименьший угол этого треугольника. Тогда
a Ј 60° и SABC = (AB · ACsin a)/2 < (2/ 4Ц3)2(Ц3/4) = 1. Получено противоречие. Треугольник, у которого
есть высота не превосходящая 4Ц3, можно поместить
в полосу шириной 4Ц3, положив сторону, на которую опущена
эта высота, на сторону полосы.
-
11.10.
-
Возведя обе части данного равенства в квадрат, его легко привести к виду
|
( |
Ц
|
ab1
|
– |
Ц
|
a1b
|
)2 + ( |
Ц
|
ca1
|
– |
Ц
|
c1a
|
)2 + ( |
Ц
|
bc1
|
– |
Ц
|
cb1
|
)2 = 0, |
|
т. е. a/a1 = b/b1 = c/c1.
-
11.11.
-
Фиксируем углы a, b и g.
Пусть A1B1C1 -
треугольник с углами a1, b1
и g1. Рассмотрим
векторы a, b и c, сонаправленные с векторами
,
и
и имеющие длины
sin a, sin b и sin g.
Тогда
|
cos a1
sin a
|
+ |
cos b1
sin b
|
+ |
cos g1
sin g
|
= – [(a, b) + (b, c) + (c, a)]/(sin asin b
sin g)
|
.
А так как 2[(a, b) + (b, c) + (c, a)] = |a + b + c|2 – |a|2 – |b|2 – |c|2,
то величина (a, b) + (b, c) + (c, a)
минимальна, когда a + b + c = 0,
т. е. a1 = a, b1 = b, g1 = g.
-
11.12.
-
Пусть x = ctg a1 и y = ctg b1. Тогда x + y > 0 (так как
a1 + b1 < p) и ctg g1 = (1 – xy)/(x + y) = (x2 + 1)/(x + y) – x.
Поэтому a2ctg a1 + b2ctg b1 + c2ctg g1 = (a2 – b2 – c2)x + b2(x + y) + c2(x2 + 1)/(x + y). При фиксированном x это выражение
минимально при таком y, что b2(x + y) = c2(x2 + 1)/(x + y), т. е.
| c/b = (x + y)/ |
Ц
|
1 + x2
|
= sin a1(ctg a1 + ctg b1) = sin g1/sin b1
|
.
Аналогичные рассуждения показывают, что если a : b : c = sin a1 : sin b1 : sin g1, то рассматриваемое
выражение минимально. В этом случае треугольники подобны
и a2ctg a + b2ctg b + c2ctg g
= 4S (см. задачу 12.44, б)).
-
11.13.
-
Пусть f = bccos x + cacos y + abcos z.
Так как cos x = – cos ycos z + sin ysin z, то f = c(a – bcos z)cos y + bcsin ysin z + abcos z.
Рассмотрим треугольник, длины двух сторон которого равны a и b,
а угол между ними равен z; пусть x и h - углы,
лежащие против сторон a и b, t - длина стороны, лежащей
против угла z. Тогда cos z = (a2 + b2 – t2)/2ab и cos h = (t2 + a2 – b2)/2at, поэтому (a – bcos z)/t = cos h. Кроме
того, b/t = sin h/sin z. Следовательно, f = ctcos (h – y) + (a2 + b2 – t2)/2.
Так как cos (h – y) Ј 1, то
| f Ј |
(a2 + b2 + c2)
2
|
– |
(c – t)2
2
|
Ј (a2 + b2 + c2)/2
|
.
Так как a і b, то x і h,а значит – x Ј – h < y – h < p – z – h = x,
т. е. cos (y – h) > cos x. Поэтому
|
f > ctcos x + |
a2 + b2 – t2
2
|
= |
c – b
2b
|
t2 + |
c(b2 – a2)
2b
|
+ |
a2 + b2
2
|
= g(t). |
|
Коэффициент при t2 отрицателен или равен нулю; кроме того,
t < a + b. Следовательно, g(t) і g(a + b) = bc + ca – ab.
-
11.14.
-
а) Так как CMXN - прямоугольник, то MN = CX. Поэтому длина
отрезка MN будет наименьшей, если CX - высота.
б) Пусть SABC = S. Тогда SAMX = AX2 · S/AB2 и SBNX = BX2 · S/AB2. Поскольку AX2 + BX2 і AB2/2 (причем
равенство достигается, только если X - середина отрезка AB),
то SCMXN = S – SAMX – SBNX Ј S/2. Площадь четырехугольника
CMXN будет наибольшей, если X - середина стороны AB.
-
11.15.
-
Точки P и Q лежат на окружности, построенной на отрезке CM
как на диаметре. В этой окружности постоянный угол C опирается
на хорду PQ, поэтому длина хорды PQ будет минимальна, если
минимален диаметр CM окружности, т. е. CM - высота
треугольника ABC.
-
11.16.
-
По теореме синусов радиусы описанных окружностей треугольников
ACM и BCM равны AC/(2sin AMC) и BC/(2sin BMC) соответственно.
Легко проверить, что sin AMC = sin BMC. Поэтому AC/(2sin AMC) + BC/(2sin BMC) = (AC + BC)/(2sin BMC). Последнее выражение будет
наименьшим, если sin BMC = 1, т. е. CM^AB.
-
11.17.
-
Точки P и Q лежат на окружности с диаметром AM, поэтому
PQ = AMsin PAQ = AMsin A. Значит, длина отрезка PQ максимальна,
когда AM - диаметр описанной окружности.
-
11.18.
-
Ясно, что 2SABC = ada + bdb + cdc. Поэтому произведение
(ada)(bdb)(cdc) будет наибольшим, если ada = bdb = cdc
(см. с. 231). Так как величина abc постоянна, произведение (ada)(bdb)(cdc) будет наибольшим тогда и только тогда, когда будет
наибольшим произведение dadbdc.
Покажем, что
равенство ada = bdb = cdc
означает, что O -
точка пересечения медиан треугольника ABC. Обозначим точку
пересечения прямых AO и BC через A1.
Тогда BA1 : A1C = SABA1 : SACA1 = SABO : SACO = (cdc) : (bdb) = 1,
т. е. AA1 - медиана. Аналогично доказывается, что точка O
лежит на медианах BB1 и CC1.
-
11.19.
-
Пусть a
= MA1/AA1, b
= MB1/BB1 и g
= MC1/CC1.
Так как a + b + g
= 1 (см. задачу 4.48, а)), то 3Ц(abg) Ј (a + b + g)/3 = 1/3, причем равенство достигается, когда
a
= b
= g
= 1/3, т. е. M - точка пересечения медиан.
-
11.20.
-
Пусть x = MA1, y = MB1 и z = MC1. Тогда ax + by + cz = 2SBMC + 2SAMC + 2SAMB = 2SABC. Поэтому
|
ж
и
|
a
x
|
+ |
b
y
|
+ |
c
z
|
ц
ш
|
· 2SABC = |
ж
и
|
a
x
|
+ |
b
y
|
+ |
c
z
|
ц
ш
|
(ax + by + cz) = a2 + b2 + c2 + ab |
ж
и
|
x
y
|
+ |
y
x
|
ц
ш
|
+ bc |
ж
и
|
y
z
|
+ |
z
y
|
ц
ш
|
+ ac |
ж
и
|
z
x
|
+ |
x
z
|
ц
ш
|
і a2 + b2 + c2 + 2ab + 2bc + 2ac
|
, причем равенство достигается , только если x = y = z,
т. е. M - центр вписанной окружности треугольника ABC.
-
11.21.
-
Предположим сначала, что все углы треугольника ABC меньше
120°. Тогда внутри его существует точка O,из которой
все стороны видны под углом 120°. Проведем через
вершины A, B и C прямые, перпендикулярные отрезкам OA, OB
и OC. Эти прямые образуют правильный треугольник A1B1C1
(рис. 11.3). Пусть Oў - любая точка, лежащая внутри треугольника
ABC и отличная от точки O. Докажем, что тогда OўA + OўB + OўC > OA + OB + OC, т. е. O - искомая точка. Пусть Aў, Bў и Cў
- основания перпендикуляров, опущенных из точки Oў на стороны
B1C1, C1A1 и A1B1, a - длина стороны правильного
треугольника A1B1C1. Тогда OўAў + OўBў + OўCў = 2(SOўB1C1 + SOўA1B1 + SOўA1C1)/a = 2SA1B1C1/a = OA + OB + OC. Так как
наклонная длиннее перпендикуляра, то OўA + OB + OўC > OўAў + OўBў + OўCў = OA + OB + OC.
Пусть теперь один из углов треугольника ABC,
например угол C,
больше 120°. Проведем через точки A
и B перпендикуляры B1C1 и C1A1 к отрезкам CA и CB,
а через точку C - прямую A1B1 перпендикулярную биссектрисе
угла ACB (рис. 11.4). Так как РAC1B = 180° – РACB < 60°, то B1C1 > A1B1. Пусть Oў - любая точка,
лежащая внутри треугольника A1B1C1. Поскольку B1C1 · OўAў + C1A1 · OўBў + A1B1 · OўCў = 2SA1B1C1,
то (OўAў + OўBў + OўCў) · B1C1 = 2SA1B1C1 + (B1C1 – A1B1) · OўCў.
Так как B1C1 > A1B1, то сумма OўAў + OўBў + OўCў минимальна
для точек, лежащих на стороне B1A1. Ясно также, что OўA + OўB + OўC і OўAў + OўBў + OўCў. Следовательно, искомой точкой является вершина C.
-
11.22.
-
Пусть расстояния от точки O до сторон BC, CA и AB равны x,
y и z соответственно. Тогда ax + by + cz = 2(SBOC + SCOA + SAOB) = 2SABC. Ясно также, что x : y : z = (SBOC/a) :
(SCOA/b) : (SAOB/c).
Уравнение ax + by + cz = 2S задает плоскость в трехмерном пространстве
с координатами x, y, z, причем вектор (a,b,c)
перпендикулярен этой плоскости, так как если ax1 + by1 + cz1 = 2S
и ax2 + by2 + cz2 = 2S, то a(x1 – x2) + b(y1 – y2) + c(z1 – z2) = 0.
Нам нужно найти точку (x0, y0, z0) этой плоскости, для которой
достигается минимум выражения x2 + y2 + z2, и проверить, что этой
точке соответствует некоторая внутренняя точка треугольника.
Так как x2 + y2 + z2 - это квадрат расстояния от начала координат
до точки (x, y, z), то искомой точкой является основание
перпендикуляра, опущенного из начала координат на плоскость,
т. е. x : y : z = a : b : c. Остается проверить,
что внутри треугольника существует точка O, для которой
x : y : z = a : b : c. Это равенство
эквивалентно условию
|
(SBOC/a) : (SCOA/b) : (SAOB/c) = a : b : c, |
|
т. е. SBOC : SCOA : SAOB = a2 : b2 : c2. А так как равенство SBOC : SAOB = a2 : c2
следует из равенств
SBOC : SCOA = a2 : b2 и SCOA : SAOB = b2 : c2,
то искомая точка - это точка пересечения прямых CC1 и AA1,
делящих стороны AB и BC в отношениях BC1 : C1A = a2 :
b2 и CA1 : A1B = b2 : c2 соответственно.
-
11.23.
-
Пусть O - вершина данного угла. Точка C является точкой
касания стороны угла с окружностью, проходящей через точки A
и B, т. е. OC2 = OA · OB. Для нахождения длины отрезка
OC достаточно провести касательную к любой окружности,
проходящей через точки A и B.
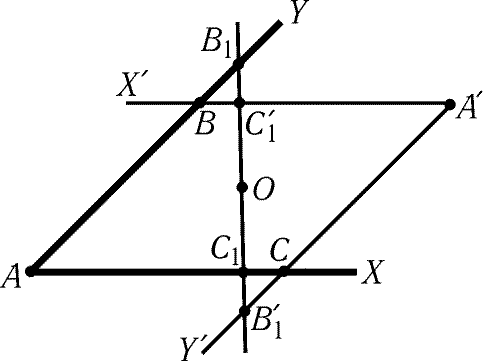
Рис. 11.5
11.24.
Рассмотрим угол XўAўYў, симметричный углу XAY относительно
точки O. Пусть B и C - точки пересечения сторон этих
углов. Обозначим точки пересечения прямой, проходящей через
точку O, со сторонами углов XAY и XўAўYў
через B1, C1
и B1ў, C1ў соответственно (рис. 11.5). Так как SAB1C1 = SAўB1ўC1ў, то SAB1C1 = (SABAўC + SBB1C1ў + SCC1B1ў)/2.
Площадь треугольника AB1C1 минимальна, если B1 = B и C1 = C,
т. е. искомой прямой является BC.
11.25.
Возьмем на сторонах OA и OB точки K и L так, что KP||OB
и LP||OA. Тогда KM : KP = PL : LN, а значит,
| KM + LN і 2 |
Ц
|
KM · LN
|
= 2 |
Ц
|
KP · PL
|
= 2 |
Ц
|
OK · OL
|
|
,
причем равенство достигается, когда
.
Ясно также, что OM + ON = (OK + OL) + (KM + LN).
-
11.26.
-
Отложим на лучах AX и AY равные отрезки AB и AC. Если
точка M лежит на отрезке BC, то сумма расстояний от нее
до прямых AB и AC равна 2(SABM + SACM)/AB = 2SABC/AB.
Поэтому сумма расстояний от точки до прямых AX и AY тем
меньше, чем меньше расстояние от ее проекции на биссектрису
угла XAY до точки A.
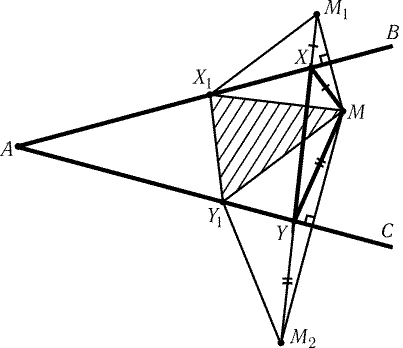
Рис. 11.6
11.27.
Пусть точки M1 и M2 симметричны M относительно прямых
AB и AC. Так как РBAM1 = РBAM и РCAM2 = РCAM, то РM1AM2 = 2РBAC < 180°. Поэтому
отрезок M1M2 пересекает лучи AB и AC в некоторых точках X
и Y (рис. 11.6). Докажем, что X и Y - искомые точки.
В самом деле, если точки X1 и Y1 лежат на лучах AB и AC,
то MX1 = M1X1 и MY1 = M2Y1, т. е. периметр треугольника MX1Y1
равен длине ломаной M1X1Y1M2. Из всех ломаных с концами
в точках M1 и M2 наименьшую длину имеет отрезок M1M2.
11.28.
Четырехугольник ABOC
наибольшей площади выпуклый. Среди всех
треугольников ABC с фиксированными углом A и стороной BC
наибольшую площадь имеет равнобедренный треугольник с основанием
BC. Значит, среди всех рассматриваемых четырехугольников
ABOC с фиксированной диагональю BC наибольшую площадь имеет
четырехугольник, для которого AB = AC, т. е. точка O лежит
на биссектрисе угла A. Рассмотрим, далее, треугольник ABO,
в котором фиксированы угол BAO, равный РA/2,
и сторона BO. Площадь этого треугольника максимальна, когда
AB = AO.
-
11.29.
-
Пусть O - точка пересечения диагоналей выпуклого четырехугольника
ABCD, а O1 - любая другая точка. Тогда AO1 + CO1 і AC = AO + CO и BO1 + DO1 і BD = BO + DO,причем хотя бы одно
из неравенств строгое. Следовательно, O - искомая точка.
-
11.30.
-
Так как SAOB : SBOC = AO : OC = SAOD : SDOC,
то SBOC · SAOD = SAOB · SDOC = 36. Следовательно,
| SBOC + SAOD і 2 |
Ц
|
SBOC · SAOD
|
= 12
|
, причем
равенство достигается, если SBOC = SAOD, т. е. SABC = SABD,
откуда AB||CD. При этом площадь четырехугольника равна 4 + 9 + 12 = 25.
-
11.31.
-
Пусть S0 и S - рассматриваемые суммы площадей треугольников
для прямой l0, проходящей через точку пересечения диагоналей
трапеции, и для некоторой другой прямой l. Легко проверить, что
S = S0 + s,
где s - площадь треугольника, образованного диагоналями
AC и BD и прямой l. Поэтому l0 - искомая прямая.
-
11.32.
-
Длины диагоналей трапеции обозначим через d1 и d2, длины
их проекций на основание - через p1 и p2, длины оснований
- через a и b, высоту - через h. Пусть
для определенности d1 і d2. Тогда p1 і p2. Ясно, что
p1 + p2 і a + b. Поэтому p1 і (a + b)/2 = S/h = 1/h. Следовательно,
| d12 = p12 + h2 і |
1
h2
|
+ h2 і 2
|
, причем равенство
достигается, только если p1 = p2 = h = 1. При этом d1 = Ц2.
-
11.33.
-
Докажем, что искомой точкой является точка M, делящая сторону
BC в отношении BM : MC = AK : KD. Обозначим точки
пересечения отрезков AM и BK, DM и CK через P, Q
соответственно. Тогда KQ : QC = KD : MC = KA : MB = KP : PB, т. е. прямая PQ параллельна основаниям трапеции.
Пусть M1 - любая другая точка на стороне BC.
Для определенности можно считать, что M1 лежит на отрезке BM.
Обозначим точки пересечения AM1 и BK, DM1 и CK, AM1
и PQ, DM1 и PQ, AM и DM1 через P1, Q1, P2,
Q2, O соответственно (рис. 11.7). Нужно доказать, что
SMPKQ > SM1P1KQ1, т. е. SMOQ1Q > SM1OPP1.
Ясно, что SMOQ1Q > SMOQ2Q = SM1OPP2 > SM1OPP1.
-
11.34.
-
Согласно задаче 4.45, а)
|
S2 = (p – a)(p – b)(p – c)(p – d) – abcdcos 2((B + D)/2). |
|
Эта величина максимальна, когда cos ((B + D)/2) = 0, т. е.
РB + РD = 180°.
-
11.35.
-
Если A и Aў - симметричные относительно точки O вершины
многоугольника, то сумма расстояний до точек A и Aў одна
и та же для всех точек отрезка AAў, а для всех других точек она
больше. Точка O принадлежит всем таким отрезкам.
-
11.36.
-
Если в треугольнике ABC угол B тупой или прямой, то по теореме
косинусов AC2 і AB2 + BC2. Поэтому, если в многоугольнике угол
при вершине B не острый, то, выбросив вершину B, получим
многоугольник с не меньшей суммой квадратов длин сторон. Так как
у любого n-угольника при n і 3 есть неострый угол, с помощью
такой операции мы приходим к треугольнику. Среди всех треугольников,
вписанных в данную окружность, наибольшую сумму квадратов длин
сторон имеет правильный треугольник (см. задачу 11.5).
-
11.37.
-
Если точка X делит некоторый отрезок PQ в отношении
l : (1 – l), то
|
®
AiX
|
= (1 – l) |
®
AiP
|
+ l |
®
AiQ
|
|
, а значит AiX Ј (1 – l)AiP + lAiQ.
Следовательно,
| f(X) = |
е
| AiX Ј (1 – l) |
е
| AiP + l |
е
| AiQ = (1 – l)f(P) + lf(Q)
|
. Пусть, например, f(P) Ј f(Q);
тогда f(X) Ј f(Q). Поэтому функция f на отрезке PQ
принимает максимальное значение в одном из его концов; точнее
говоря, внутри отрезка не может быть точки строгого максимума
функции f. Следовательно, если X - любая точка
многоугольника, то f(X) Ј f(Y), где Y - некоторая точка
стороны многоугольника, а f(Y) Ј f(Z), где Z -
некоторая вершина.
-
11.38.
-
Геометрическое место точек X, для которых угол OXA постоянен,
состоит их двух симметричных относительно прямой OA дуг
окружностей S1 и S2. Рассмотрим тот случай, когда диаметр
окружностей S1 и S2 равен радиусу исходной окружности,
т. е. эти окружности касаются исходной окружности в точках M1
и M2,
для которых РOAM1 = РOAM2 = 90°.
Точки M1 и M2 являются искомыми, так как если РOXA > РOM1A = РOM2A, то точка X лежит строго внутри
фигуры, образованной окружностями S1 и S2, т. е. не может
лежать на исходной окружности.
-
11.39.
-
Обозначим точку пересечения прямой l и отрезка AB через O.
Рассмотрим произвольную окружность S, проходящую через точки A
и B. Она пересекает l в некоторых точках M и N. Поскольку
MO · NO = AO · BO - постоянная величина,
то
|
MN = MO + NO і 2 |
Ц
|
MO · NO
|
= 2 |
Ц
|
AO · BO
|
, |
|
причем равенство достигается, только если MO = NO. В этом случае
центр окружности S является точкой пересечения серединного
перпендикуляра к AB и перпендикуляра к l, проходящего через
точку O.
-
11.40.
-
Построим окружность с диаметром PQ. Если эта окружность
пересекается с прямой l, то любая из точек пересечения является
искомой, поскольку в этом случае Pў = Qў. Если же окружность
не пересекается с прямой l, то для любой точки M
на прямой l угол PMQ острый и РPўPQў = 90°±РPMQ. Теперь легко убедиться, что длина хорды PўQў минимальна,
если угол PMQ максимален. Для нахождения точки M остается
провести через точки P и Q окружности, касающиеся
прямой l (см. задачу 8.56, а)), и из точек касания выбрать нужную.
-
11.41.
-
Пусть сумма расстояний от точек A и B до прямой l равна 2h.
Если прямая l пересекает отрезок AB в точке X, то SAOB = h · OX, поэтому величина h экстремальна, когда экстремальна
величина OX, т. е. прямая OX соответствует стороне или высоте
треугольника AOB. Если прямая l не пересекает отрезок AB,
то величина h равна средней линии трапеции, ограниченной
перпендикулярами, опущенными из точек A и B на прямую l.
Эта величина экстремальна, когда прямая l перпендикулярна
медиане OM треугольника AOB или соответствует стороне
треугольника AOB. Остается выбрать две из полученных четырех прямых.
-
11.42.
-
Предположим сначала, что точки являются вершинами выпуклого
пятиугольника. Сумма углов пятиугольника равна 540°,
поэтому один из его углов не превосходит 540°/5 = 108°.
Диагонали делят этот угол на три угла, поэтому один из них
не превосходит 108°/3 = 36°. В этом случае a Ј 36°.
Если точки не являются вершинами выпуклого пятиугольника, то одна из них
лежит внутри треугольника, образованного тремя другими. Один
из углов этого треугольника не превосходит 60°. Отрезок,
соединяющий соответствующую вершину с внутренней точкой, делит
этот угол на два угла, поэтому один из них не превосходит 30°.
В этом случае a Ј 30°.
Во всех случаях a Ј 36°.
Ясно, что для правильного пятиугольника a = 36°.
-
11.43.
-
Замкнутый маршрут, проходящий через все перекрестки, может иметь 20
поворотов (рис. 11.8). Остается доказать, что меньше 20 поворотов
такой маршрут иметь не может. После каждого поворота происходит
переход с горизонтальной улицы на вертикальную или с вертикальной
на горизонтальную. Поэтому число горизонтальных звеньев замкнутого
маршрута равно числу вертикальных звеньев и равно половине числа
поворотов. Предположим, что замкнутый маршрут имеет меньше 20
поворотов. Тогда найдутся улицы обоих направлений, по которым
маршрут не проходит. Поэтому маршрут не проходит через перекресток
этих улиц.
-
11.44.
-
Прямая может пересекать 15 клеток (рис. 11.9). Докажем теперь, что
прямая не может пересекать более 15 клеток. Число клеток, которые
пересекает прямая, на 1 меньше числа точек пересечения ее с отрезками,
задающими стороны клеток. Внутри квадрата имеется 14 таких
отрезков. Поэтому внутри квадрата не более 14 точек пересечения
прямой со сторонами клеток. Никакая прямая не может пересекать
границу доски более чем в двух точках, поэтому число точек
пересечения ее с отрезками не превышает 16. Следовательно,
наибольшее число клеток шахматной доски размером 8×8,
которые можно пересечь одной прямой, равно 15.
-
11.45.
-
Докажем сначала, что 33 точки разместить таким образом нельзя.
Действительно, если на отрезке длиной 1 находятся 33 точки,
то расстояние между какими-нибудь двумя из них не превосходит 1/32.
Отрезок с концами в этих точках содержит две точки, а он должен
содержать не более 1 + 1000/322 точек, т. е. менее двух точек.
Докажем теперь, что 32 точки разместить можно. Возьмем 32 точки,
делящие отрезок на равные части (концы данного отрезка входят
в число этих 32 точек). Тогда отрезок длиной d содержит либо [31d],
либо [31d] + 1 точек. Нужно доказать, что [31d] Ј 1000 d2.
Если 31d < 1, то [31d] = 0 < 1000 d2. Если 31d і 1,
то [31d] Ј 31d Ј (31d)2 = 961 d2 < 1000d2.
Примечание.
[x] - целая часть числа x, т. е. наибольшее целое число,
не превосходящее x.
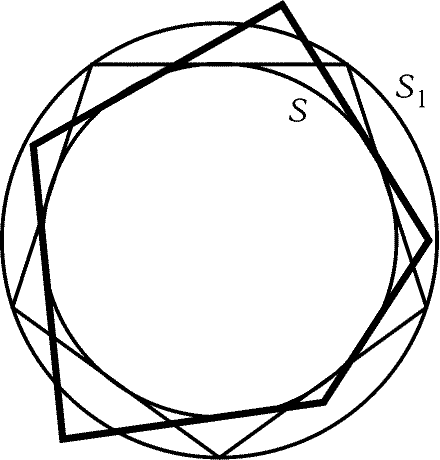
Рис. 11.10
11.46.
а) Пусть неправильный n-угольник описан около окружности S.
Опишем около этой окружности правильный n-угольник, а около
него опишем окружность S1 (рис. 11.10). Докажем, что площадь
части неправильного n-угольника, заключенной внутри S1,
больше площади правильного n-угольника. Все касательные
к S отсекают от S1 равные сегменты. Поэтому сумма площадей
сегментов, отсекаемых от S1 сторонами правильного n-угольника,
равна сумме площадей сегментов, отсекаемых от S1 сторонами
неправильного n-угольника или их продолжениями. Но для правильного
n-угольника эти сегменты не пересекаются (точнее говоря, не имеют
общих внутренних точек), а для неправильного n-угольника
некоторые из них обязательно перекрываются, поэтому площадь
объединения этих сегментов для правильного n-угольника
больше, чем для неправильного. Следовательно, площадь части
неправильного n-угольника, заключенной внутри окружности S1,
больше площади правильного n-угольника, а площадь всего
неправильного n-угольника и подавно больше площади правильного.
б) Эта задача следует из а), так как периметр многоугольника,
описанного около окружности радиуса R, равен 2S/R, где S
- площадь многоугольника.
-
11.47.
-
Стороны треугольника ABC пропорциональны sin a, sin b
и sin g. Если угол g фиксирован, то величина |sin a – sin b| = 2|sin ((a – b)/2)sin (g/2)| тем больше, чем больше
величина j
= |a – b|. Остается заметить, что величины
S = 2R2 sin asin bsin g
= R2 sin g(cos (a – b) + cos g) = R2 sin g(cos j + cos g) и sin a + sin b
= 2cos (g/2)cos (j/2) монотонно убывают при возрастании j.
-
11.48.
-
а) Обозначим длину стороны правильного n-угольника, вписанного
в данную окружность, через an. Рассмотрим произвольный неправильный
n-угольник, вписанный в эту окружность. У него обязательно
найдется сторона длиной меньше an. А вот стороны длиной больше an
у него может и не быть, но тогда этот многоугольник можно заключить
в сегмент, отсекаемый стороной правильного n-угольника. Так
как при симметрии относительно стороны правильного n-угольника
сегмент, отсекаемый этой стороной, попадает внутрь n-угольника,
площадь n-угольника больше площади сегмента. Поэтому можно считать,
что у рассматриваемого n-угольника есть сторона длиной
меньше an и сторона длиной больше an.
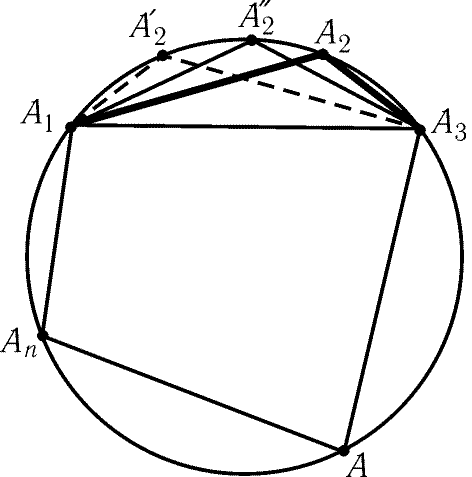
Рис. 11.11
Мы можем поменять местами соседние стороны n-угольника, т. е.
вместо многоугольника
A1A2A2јAn
взять многоугольник
A1A2ўA3јAn,
гдеточка A2ў симметрична точке A2
относительно серединного перпендикуляра к отрезку A1A3
(рис. 11.11). При этом оба многоугольника вписаны в одну и ту же
окружность и их площади равны. Ясно, что с помощью этой операции
можно сделать соседними любые две стороны многоугольника. Поэтому
будем считать, что у рассматриваемого n-угольника A1A2 > an
и A2A3 < an.
Пусть A2ў - точка, симметричная точке A2
относительно серединного перпендикуляра к отрезку A1A3. Если
точка A2ўў лежит на дуге A2A2ў, то разность углов
при основании A1A3 у треугольника A1A2ўўA3 меньше, чем
у треугольника A1A2A3, так как величины углов A1A3A2ўў
и A3A1A2ўў заключены между величинами углов A1A3A2
и A3A1A2. Поскольку A1A2ў < an и A1A2 > an, то на дуге
A2A2ў существует точка A2ўў, для которой A1A2ўў = an.
Площадь треугольника A1A2ўўA3 больше площади треугольника
A1A2A3 (см. задачу 11.47, а)). Площадь многоугольника
A1A2ўўA3јAn больше площади исходного многоугольника,
и у него по крайней мере на 1 больше число сторон, равных an.
За конечное число шагов мы придем к правильному n-угольнику,
причем каждый раз площадь увеличивается. Следовательно, площадь
любого неправильного n-угольника, вписанного в окружность,
меньше площади правильного n-угольника, вписанного в ту же
окружность.
б) Доказательство аналогично предыдущему, нужно только воспользоваться
результатом задачи 11.47, б), а не задачи 11.47, а).
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:45.

 Глава 11. Задачи для самостоятельного решения |
Глава 11. Задачи для самостоятельного решения | 

 Глава 11. Задачи для самостоятельного решения |
Глава 11. Задачи для самостоятельного решения |