| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
§ 1. Теорема синусов
-
12.1.
-
Докажите, что площадь S треугольника равна abc/4R.
-
12.2.
-
Точка D лежит на основании AC равнобедренного
треугольника ABC. Докажите, что радиусы описанных окружностей
треугольников ABD и CBD равны.
-
12.3.
-
Выразите площадь треугольника ABC через длину
стороны BC и величины углов B и C.
-
12.4.
-
Докажите, что
|
|
a + b
c
|
= cos |
a – b
2
| / |
sin |
g
2
|
, и |
a – b
c
|
= sin |
a – b
2
| / |
cos |
g
2
|
. |
|
-
12.5.
-
В остроугольном треугольнике ABC проведены
высоты AA1 и CC1. Точки A2 и C2 симметричны A1 и C1
относительно середин сторон BC и AB. Докажите, что прямая,
соединяющая вершину B с центром O описанной окружности, делит
отрезок A2C2 пополам.
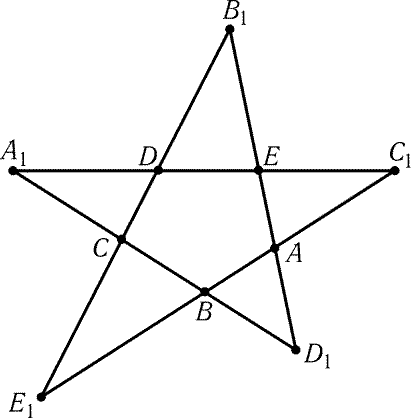
Рис. 12.1
12.6. Через точку S проведены прямые a,b,c и d;
прямая l пересекает их в точках A,B,C и D. Докажите, что
величина AC · BD/(BC · AD) не зависит от выбора прямой l.
12.7. Даны прямые a и b, пересекающиеся в точке O,
и произвольная точка P. Прямая l, проходящая через точку P,
пересекает прямые a и b в точках A и B. Докажите, что
величина (AO/OB)/(PA/PB) не зависит от выбора прямой l.
12.8. Обозначим вершины и точки звеньев (неправильной)
пятиконечной звезды так, как показано на рис. 12.1. Докажите, что
|
A1C · B1D · C1E · D1A · E1B = A1D · B1E · C1A · D1B · E1C. |
|
-
12.9.
-
Два подобных равнобедренных треугольника имеют общую
вершину. Докажите, что проекции их оснований на прямую, соединяющую
середины оснований, равны.
-
12.10*.
-
На окружности с диаметром AB взяты точки C и D.
Прямая CD и касательная к окружности в точке B пересекаются
в точке X. Выразите BX через радиус окружности R
и углы j
= РBAC и y = РBAD.
Глава 12 | 
