Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!)	МЦНМО, 2002


Глава 17. Задачи для самостоятельного решения \|	Оглавление \|	Глава 18.

Решения

17.1.: Обозначим точки, симметричные точкам C и D относительно прямой AB, через Cў и Dў соответственно. РCўMD = 90°, поэтому CM² + MD² = CўM² + MD² = CўD². Поскольку РCўCD = 45°, хорда CўD имеет постоянную длину.

17.2.: Проведем диаметр окружности S, являющийся осью симметрии окружностей S₁ и S₂. Пусть точки Cў и B₂ў симметричны точкам C и B₂ относительно этого диаметра (рис. 17.1).

Окружности S₁ и S гомотетичны с центром гомотетии в точке A₁, причем при этой гомотетии прямая B₁B₂ў переходит в прямую CCў, поэтому эти прямые параллельны. Ясно также, что B₂B₂ў||CCў. Поэтому точки B₁, B₂ў и B₂ лежат на одной прямой, причем эта прямая параллельна прямой CCў.

17.3.

Пусть прямая, симметричная прямой A₁B₁ относительно прямой AB, пересекает стороны CA и CB (или их продолжения) в точках A₂ и B₂. Так как РA₁AM = РB₂BM и РA₁MA = РB₂MB, то DA₁AM ~ DB₂BM, т. е. A₁A : A₁M = B₂B : B₂M. Кроме того, так как MB - биссектриса треугольника B₁MB₂, то B₂B : B₂M = B₁B : B₁M.

Рис. 17.1

Рис. 17.2

17.4.: Предположим, что четырехугольник ABCD построен. Пусть для определенности AD > AB. Обозначим через Bў точку, симметричную точке B относительно диагонали AC. Точка Bў лежит на стороне AD, причем BўD = AD – AB. В треугольнике BўCD известны длины всех сторон: BўD = AD – AB и BўC = BC. Построив треугольник BўCD, на продолжении стороны BўD за точку Bў построим точку A. Дальнейшее построение очевидно.

17.5.: Предположим, что четырехугольник ABCD построен. Для определенности будем считать, что AD > AB. Пусть O - центр вписанной окружности; точка Dў симметрична D относительно прямой AO; Aў — точка пересечения прямых AO и DC, Cў - точка пересечения прямых BC и AўDў (рис. 17.2).

В треугольнике BCўDў известны сторона BDў и прилегающие к ней углы РDўBCў = 180° – РB и РBDўCў = РD. Построим треугольник BCўDў по этим элементам. Так как ADў = AD, то можно построить точку A. Затем строим точку O пересечения биссектрис углов ABCў и BDўCў. Зная положение точки O, можно построить точку D и вписанную окружность. Точка C является точкой пересечения прямой BCў и касательной к окружности, проведенной из точки D.

17.6.: Предположим, что треугольник ABC построен. Пусть Cў - точка, симметричная точке C относительно серединного перпендикуляра к отрезку AB. В треугольнике ACCў известны AC = b, ACў = a и РCACў = РA – РB. Поэтому его можно построить. Точка B симметрична точке A относительно серединного перпендикуляра к отрезку CCў.

17.7.: Предположим, что треугольник ABC построен. Обозначим через Cў точку, симметричную C относительно серединного перпендикуляра к стороне AB, через Bў - точку, симметричную B относительно прямой CCў. Для определенности будем считать, что AC < BC. Тогда РACBў = РACCў + РCўCB = 180° – РA + РCўCB = 180° – (РA – РB), т. е. угол ACBў известен.

Треугольник ABBў можно построить, так как AB = c, BBў = 2h_c и РABBў = 90°. Точка C является точкой пересечения серединного перпендикуляра к отрезку BBў и дуги окружности, из которой отрезок ABў виден под углом 180° – (РA – РB).

17.8.: а) Предположим, что треугольник ABC построен. Пусть Cў - точка, симметричная точке A относительно биссектрисы угла C. Тогда РBCўA = 180° – РACўC = 180° – (180° – РC)/2 = 90° + РC/2 и BCў = a – b.

В треугольнике ABC известны AB = c, BCў = a – b и РCў = 90° + РC/2. Так как РCў > 90°, треугольник ABCў строится по этим элементам однозначно. Точка C является точкой пересечения серединного перпендикуляра к отрезку ACў и прямой BCў.

б) Решение аналогично решению задачи а). В качестве Cў нужно взять точку, симметричную точке A относительно биссектрисы внешнего угла C треугольника ABC. Так как РACўB = РC/2 < 90°, задача может иметь два решения.

17.9.: Пусть S - окружность радиуса a с центром B, Sў - окружность радиуса AX с центром X, Aў - точка, симметричная точке A относительно прямой l. Тогда окружность Sў касается окружности S, а точка Aў лежит на окружности Sў. Остается провести через данные точки A и Aў окружность Sў, касающуюся данной окружности S, и найти ее центр X (см. задачу 8.56, б)).

17.10.: Пусть проекция точки A на прямую ON лежит ближе к точке O, чем проекция точки B. Предположим, что равнобедренный треугольник XYZ построен.

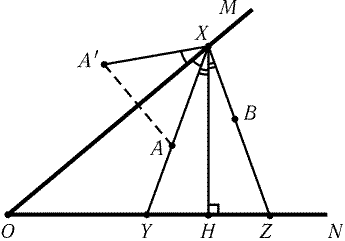
Рис. 17.3

Рассмотрим точку Aў, симметричную точке A относительно прямой OM. Опустим из точки X перпендикуляр XH на прямую ON (рис. 17.3). Так как РAўXB = РAўXO + РOXA + РYXH + РHXZ = 2РOXY +
+ 2РYXH = 2РOXH = 180° – 2РMON, то угол AўXB известен. Точка X является точкой пересечения прямой OM и дуги, из которой отрезок AўB виден под углом 180° – 2РMON. При этом проекция точки X на прямую ON должна лежать между проекциями точек A и B.

Обратно, если РAўXB = 180° – РMON и проекция точки X на прямую ON лежит между проекциями точек A и B, то треугольник XYZ равнобедренный.

17.11.: Предположим, что точка X построена. Пусть Bў - точка, симметричная точке B относительно прямой MN; окружность радиуса ABў с центром Bў пересекает прямую MN в точке Aў. Тогда луч BўX является биссектрисой угла ABўAў. Следовательно, X - точка пересечения прямых BўO и MN, где O - середина отрезка AAў.

17.12.: Проведем через точку A₁ прямую BC, перпендикулярную прямой l₁. Вершина A искомого треугольника ABC является точкой пересечения прямых, симметричных прямой BC относительно прямых l₂ и l₃.

17.13.: Пусть точка Aў симметрична точке A относительно биссектрисы угла C. Тогда C - точка пересечения прямой AўB и прямой, на которой лежит биссектриса угла C.

17.14.: Пусть A₂ и A₃ - точки, симметричные точке A относительно прямых l₂ и l₃. Тогда точки A₂ и A₃ лежат на прямой BC. Поэтому точки B и C являются точками пересечения прямой A₂A₃ с прямыми l₂ и l₃.

17.15.: Предположим, что треугольник ABC построен, причем N - середина AC, M - середина BC и биссектриса угла A лежит на данной прямой l. Построим точку Nў, симметричную N относительно прямой l. Прямая BA проходит через точку Nў и параллельна прямой MN. Таким образом мы находим вершину A и прямую BA. Проведя прямую AN, получим прямую AC. Остается построить отрезок, концы которого лежат на сторонах угла BAC и M - его середина (см. решение задачи 16.15).

17.16.: Пусть точки Aў и Bў симметричны A и B относительно прямой CM. Тогда AM + MB = AўM + MB > AўB = AўC + CB = AC + CB.

17.17.: Пусть точки Bў, Cў и Mў симметричны точкам B, C и M относительно биссектрисы внешнего угла при вершине A. Тогда AM + AMў і MMў = (BBў + CCў)/2 = (b + c)sin (90° – (a/2)) = (b + c)cos (a/2).

17.18.: Пусть точка Bў симметрична B относительно биссектрисы угла ACB. Тогда BўA₁ = BB₁, т. е. требуется проверить, что BўA₁ < AA₁. Для этого достаточно заметить, что РABўA₁ > РABўB > 90°.

17.19.: Пусть Dў - точка, симметричная точке D относительно серединного перпендикуляра к отрезку AC. Тогда S_ABCD = S_ABCDў = S_BADў + S_BCDў Ј AB · ADў/2 + BC · CDў/2 = (AB · CD + BC · AD)/2.

17.20.: Пусть точка Aў симметрична точке A относительно прямой l. Пусть X - точка на прямой l. Тогда AX + XB = AўX + XB і AўB, причем равенство достигается, только если точка X лежит на отрезке AўB. Поэтому искомая точка является точкой пересечения прямой l и отрезка AўB.

17.21.: Пусть PQR - треугольник, образованный основаниями высот треугольника ABC, PўQўRў - любой другой треугольник, вписанный в треугольник ABC. Пусть, далее, точки P₁ и P₂ (соответственно, P₁ў и P₂ў) симметричны точке P (соответственно Pў) относительно прямых AB и AC (рис. 17.4). Точки Q и R лежат на отрезке P₁P₂ (см. задачу 1.58), поэтому периметр треугольника PQR равен длине отрезка P₁P₂. А периметр треугольника PўQўRў равен длине ломаной P₁ўRўQўP₂ў, т. е. он не меньше длины отрезка P₁ўP₂ў. Остается заметить, что (P₁ўP₂ў)² = P₁P₂² + 4d², где d - расстояние от точки P₁ў до прямой P₁P₂.

Рис. 17.4

17.22.: Пусть X - произвольная точка, X₁ = S_l₁(X) и X₂ = S_l₂(X₁).

а) Выберем на прямой l₁ произвольную точку O и рассмотрим систему координат с началом O и осью абсцисс, направленной по прямой l₁. Прямая l₂ задается в этой системе координат уравнением y = a. Пусть y, y₁ и y₂ - ординаты точек X, X₁ и X₂. Ясно, что y₁ = – y и y₂ = (a – y₁) + a = y + 2a. Так как точки X, X₁ и X₂ имеют одинаковые абсциссы, то X₂ = T_2a(X), где T_a - перенос, переводящий l₁ в l₂, причем a^l₁.

б) Рассмотрим систему координат с началом O и осью абсцисс, направленной по прямой l₁. Пусть угол поворота от прямой l₁ к l₂ в этой системе координат равен a, углы поворотов от оси абсцисс до лучей OX, OX₁ и OX₂ равны j, j₁ и j₂. Ясно, что j₁ = – j и j₂ = (a – j₁) + a = j + 2a. Так как OX = OX₁ = OX₂, то X₂ = R^2a_O(X), где R^a_O - поворот, переводящий l₁ в l₂.

17.23.

Представим T°T в виде композиции трех преобразований:

T°T = (S_a°S_b°S_c)°(S_a°S_b°S_c) = (S_a°S_b)°(S_c°S_a)°(S_b°S_c).

При этом S_a°S_b, S_c°S_a и S_b°S_c - повороты на углы 2Р(b, a), 2Р(a, c) и 2Р(c, b) соответственно. Сумма углов поворотов равна 2(Р(b, a) + Р(a, c) + Р(c, b)) = 2Р(b, b) = 0°, причем эта величина определена с точностью до 2 · 180° = 360°. Следовательно, эта композиция поворотов является параллельным переносом (см. задачу 18.35).

17.24.: Если точки X и Y симметричны относительно прямой l₃, то точки S_l₁(X) и S_l₁(Y) симметричны относительно прямой l₂, т. е. S_l₁(X) = S_l₂°S_l₁(Y). Поэтому S_l₁°S_l₃ = S_l₂°S_l₁ и S_l₃ = S_l₁°S_l₂°S_l₁.

17.25.: Пусть O - центр вписанной окружности; a и b - прямые OA и OB. Тогда S_a°S_b(C₁) = S_a(A₁) = A₂ и S_b°S_a(C₁) = S_b(B₁) = B₂. Точки A₂ и B₂ получаются из точки C₁ поворотами с центром O на противоположные углы, поэтому A₂B₂||AB. Аналогичные рассуждения показывают, что стороны треугольников ABC и A₂B₂C₂ параллельны, а значит, эти треугольники гомотетичны. Прямые AA₂, BB₂ и CC₂ проходят через центр гомотетии, переводящей треугольник ABC в A₂B₂C₂. Заметим, что при этой гомотетии описанная окружность треугольника ABC переходит в его вписанную окружность, т. е. центр гомотетии лежит на прямой, соединяющей центры этих окружностей.

17.26.: Для каждого вектора прыжка имеется ровно два положения кузнечика, для которых прыжок задается этим вектором. Поэтому последовательность прыжков периодична тогда и только тогда, когда имеется лишь конечное число различных векторов прыжков.

Пусть a₁ - вектор прыжка кузнечика с прямой l₂ на прямую l₁; a₂, a₃, a₄, ј - векторы последующих прыжков. Тогда a₂ = S_l₂(a₁), a₃ = S_l₁(a₂), a₄ = S_l₂(a₃), ј Так как композиция S_l₁°S_l₂ является поворотом на угол 2g (или на угол 2p – 2g), векторы a₃, a₅, a₇, ј получаются из вектора a₁ поворотами на 2g, 4g, 6g, ј (или на 2(p – g), 4(p – g), 6(p – g), ј). Поэтому набор a₁, a₃, a₅, ј содержит конечное число различных векторов тогда и только тогда, когда g/p - рациональное число. Набор a₂, a₄, a₆, ј рассматривается аналогично.

17.27.: а) Предположим, что многоугольник A₁A₂јA_n построен. Проведем через центр O окружности серединные перпендикуляры l₁, l₂, ј, l_n к хордам A₁A₂, A₂A₃, ј, A_nA₁ соответственно. Прямые l₁, ј, l_n известны, так как они проходят через точку O и перпендикулярны данным прямым. Кроме того, A₂ = S_l₁(A₁), A₃ = S_l₂(A₂), ј, A₁ = S_{l_n}(A_n), т. е. точка A₁ является неподвижной точкой композиции симметрий S_{l_n}°ј°S_l₁. При нечетном n на окружности неподвижных точек ровно две; при четном n либо неподвижных точек нет, либо все точки неподвижны.

б) Предположим, что искомый многоугольник A₁јA_n построен. Рассмотрим многоугольник B₁јB_n, образованный точками касания описанного многоугольника с окружностью. Стороны многоугольника B₁јB_n перпендикулярны данным прямым, т. е. имеют заданные направления, поэтому его можно построить (см. задачу а)); остается провести касательные к окружности в точках B₁, ј, B_n.

17.28.: Рассмотрим композицию последовательных симметрий относительно данных прямых l₁, ј, l_n. В задаче а) в качестве вершины A₁ искомого n-угольника нужно взять неподвижную точку этой композиции, а в задаче б) в качестве прямой A₁A_n нужно взять неподвижную прямую.

17.29.: При последовательных симметриях относительно прямых L₁, ј, l_n – 1, перпендикулярных данным прямым и проходящих через центр окружности, вершина A₁ искомого многоугольника переходит в вершину A_n. Если n нечетно, то композиция этих симметрий - поворот на известный угол, поэтому через точку M нужно провести хорду A₁A_n известной длины. Если n четно, то рассматриваемая композиция является симметрией относительно некоторой прямой, поэтому из точки M нужно опустить перпендикуляр на эту прямую.

17.30.: Пусть O - центр данного круга, D_R - круг радиуса R с центром O. Докажем, что множеством образов точек D_R при симметриях относительно прямых, проходящих через D₁, является круг D_R + 2. В самом деле, образы точки O при указанных симметриях заполняют круг D₂, а круги радиуса R с центрами в D₂ заполняют круг D_R + 2. Поэтому за n отражений из точек D₁ можно получить любую точку из D_2n + 1 и только эти точки. Остается заметить, что точку A можно «загнать» внутрь D_R за n отражений тогда и только тогда, когда за n отражений можно перевести некоторую точку из D_R в A.

17.31.: Обозначим симметрии относительно прямых OA₁, ј, OA_n через S_!, ј, S_n. Пусть X_k = S_k(X) при k = 1, ј, n. Нужно доказать, что при некотором повороте относительно точки O система точек X₁, ј, X_n переходит в себя. Ясно, что S_k + 1°S_k(X_k) = S_k + 1°S_k°S_k(X) = X_k + 1. Преобразования S_k + 1°S_k являются поворотами относительно точки O на угол 4p/n (см. задачу 17.22, б)).

Замечание. При четном n получается n/2-угольник.

17.32.: Пусть прямые l₁ и l₂ являются осями симметрии плоской фигуры. Это означает, что если точка X принадлежит фигуре, то точки S_l₁(X) и S_l₂(X) принадлежат фигуре. Рассмотрим прямую l₃ = S_l₁(l₂). Согласно задаче 17.24 S_l₃(X) = S_{l_!}°S_l₂°S_l₁(X), поэтому l₃ также является осью симметрии.

Если у фигуры ровно две оси симметрии, то l₃ = l₁ или l₃ = l₂. Ясно, что l₃ № l₁, поэтому l₃ = l₂, т. е. прямая l₂ перпендикулярна прямой l₁.

17.33.: Предположим, что многоугольник имеет три оси симметрии, которые не пересекаются в одной точке, т. е. они образуют треугольник. Пусть X - точка многоугольника, наиболее удаленная от некоторой внутренней точки M этого треугольника. Точки X и M лежат по одну сторону от одной из рассматриваемых осей симметрии l. Если Xў - точка, симметричная X относительно прямой l, то MXў > MX и точка Xў более удалена от точки M, чем точка X. Получено противоречие, поэтому все оси симметрии многоугольника пересекаются в одной точке.

17.34.: Все оси симметрии проходят через одну точку O (задача 17.33). Если l₁ и l₂ — оси симметрии, то l₃ = S_l₁(l₂) - тоже ось симметрии (см. задачу 17.24). Выберем одну из осей симметрии l нашего многоугольника. Остальные оси разбиваются на пары прямых, симметричных относительно l. Если прямая l₁, перпендикулярная l и проходящая через точку O, не является осью симметрии, то число осей симметрии нечетно. Поэтому прямая l₁ является осью симметрии. Ясно, что S_l₁°S_l = R_O^180° — центральная симметрия, т. е. O — центр симметрии.

17.35.: Пусть F — движение, переводящее точку A в Aў, причем точки A и Aў не совпадают; S симметрия относительно серединного перпендикуляра l к отрезку AAў. Тогда S°F(A) = A, т. е. A - неподвижная точка преобразования S°F. Кроме того, если X - неподвижная точка преобразования F, то AX = AўX, т. е. точка X лежит на прямой l, а значит, X — неподвижная точка преобразования S°F. Таким образом, точка A и все неподвижные точки преобразования F являются неподвижными точками преобразования S°F.

Возьмем точки A, B и C, не лежащие на одной прямой, и рассмотрим их образы при данном движении G. Можно построить такие преобразования S₁, S₂ и S₃, являющиеся симметриями относительно прямых или тождественными преобразованиями, что преобразование S₃°S₂°S₁°G оставляет неподвижными точки A, B и C, т. е. оно является тождественным преобразованием E. Домножая равенство S₃°S₂°S₁°G = E слева последовательно на S₃, S₂ и S₁ и учитывая, что S_i°S_i = E, получаем G = S₁°S₂°S₃.

17.36.: Согласно задаче 17.35 любое движение первого рода является композицией двух симметрий относительно прямых. Остается воспользоваться результатом задачи 17.22.

17.37.: Согласно задаче 17.35 любое движение второго рода можно представить в виде S₃°S₂°S₁, где S₁, S₂ и S₃ — симметрии относительно прямых l₁, l₂ и l₃. Предположим сначала, что прямые l₂ и l₃ не параллельны. Тогда при повороте прямых l₂ и l₃ относительно точки их пересечения на любой угол композиция S₃°S₂ не изменяется (см. задачу 17.22. б)), поэтому можно считать, что l₂^l₁. Остается повернуть прямые l₁ и l₂ относительно точки их пересечения так, чтобы прямая l₂ стала параллельна прямой l₃.

Предположим теперь, что l₂||l₃. Если прямая l₁ не параллельна этим прямым, то прямые l₁ и l₂ можно повернуть относительно точки их пересечения так, что прямые l₂ и l₃ станут не параллельны. А если l₁||l₂, то прямые l₁ и l₂ можно перенести параллельно так, что прямые l₂ и l₃ совпадут.

Глава 17. Задачи для самостоятельного решения \|	Оглавление \|	Глава 18.

Внимание! Данное издание содержит опечатки!
Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора.
Заказ книги: biblio@mccme.ru.