| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
19.1.
-
При гомотетии с центром в точке пересечения диагоналей
четырехугольника и коэффициентом 3/2 точки пересечения медиан
указанных треугольников переходят в середины сторон четырехугольника.
Остается воспользоваться результатом задачи 1.2.
-
19.2.
-
При гомотетии с центром K, переводящей DKBC в
DKAD, точка M переходит в N, поэтому точка K лежит
на прямой MN. При гомотетии с центром L, переводящей
DLBC в DLDA, точка M переходит в N.
Поэтому точка L лежит на прямой MN.
-
19.3.
-
Пусть продолжения боковых сторон AB и CD пересекаются
в точке K, а диагонали трапеции пересекаются в точке L. Согласно
предыдущей задаче прямая KL проходит через середину отрезка
AD, а по условию задачи эта же прямая делит пополам угол
AKD. Поэтому треугольник AKD равнобедренный (см. задачу 16.1),
а значит, трапеция ABCD тоже равнобедренная.
-
19.4.
-
При гомотетии с центром M и коэффициентом – 2 прямые
PA1, PB1 и PC1 переходят в прямые la, lb и lc,
а значит, искомая точка Q является образом точки P при этой
гомотетии.
-
19.5.
-
Рассмотрим гомотетию HBk с центром B, переводящую
отрезок AC в отрезок AўCў, касающийся описанной окружности
треугольника ABC. Обозначим середины отрезков PK и AўCў через O1
и D, центр окружности S - через O.
Окружность S является вписанной окружностью треугольника AўBCў,
поэтому достаточно доказать, что при гомотетии HBk точка O1
переходит в O. Для этого достаточно проверить, что BO1 :
BO = BA : BAў. Это равенство следует из того, что PO1 и DA
- высоты подобных прямоугольных треугольников BPO и BDAў.
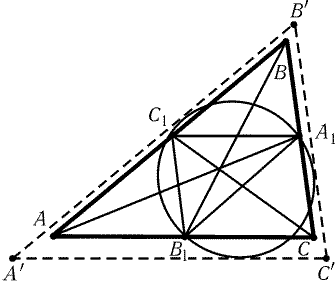
Рис. 19.1
19.6.
Пусть k - коэффициент подобия многоугольников, причем
k < 1. Сдвигая стороны исходного многоугольника внутрь последовательно
на k, k2, k3, ј, получаем стягивающуюся систему вложенных
выпуклых многоугольников, подобных исходному с коэффициентами k, k2,
k3, ј Единственная общая точка этих многоугольников
является центром вписанной окружности исходного многоугольника.
19.7.
Пусть A1, B1 и C1 - середины сторон BC, AC и AB
соответственно. При гомотетии с центром в точке пересечения
медиан треугольника и коэффициентом гомотетии – 1/2 описанная
окружность S треугольника ABC переходит в описанную окружность S1
треугольника A1B1C1. Так как окружность S1 пересекает
все стороны треугольника ABC, то можно построить треугольник
AўBўCў со сторонами, параллельными сторонам треугольника ABC,
для которого S1 будет вписанной окружностью (рис. 19.1). Пусть r
и rў - радиусы вписанных окружностей треугольников ABC и AўBўCў;
R и R1 - радиусы окружностей S и S1. Ясно, что
r Ј rў = R1 = R/2. Равенство достигается, если треугольники AўBўCў
и ABC совпадают, т. е. S1 - вписанная окружность треугольника
ABC. В этом случае AB1 = AC1, поэтому AB = AC. Аналогично AB = BC.
19.8.
Так как
|
®
MMi
|
= ( |
®
MA1
|
+ ј + |
®
MAn
|
– |
®
MAi
|
)/(n – 1) = – |
®
MAi
|
/(n – 1)
|
, то точка Ai переходит в точку Mi при
гомотетии с центром M и коэффициентом – 1/(n – 1).
19.9.
Пусть A и B - пара наиболее удаленных друг от друга
точек многоугольника F. Тогда F1 = HA1/2(F) и
F2 = HB1/2(F) - искомые фигуры. В самом деле, F1
и F2 не пересекаются, так как лежат по разные стороны от
серединного перпендикуляра к отрезку AB. Кроме того, Fi
содержится в F, так как F - выпуклый многоугольник.
19.10.
Пусть M - точка пересечения медиан треугольника ABC,
O - середина отрезка AB. Ясно, что
,
поэтому точки M заполняют окружность, полученную из исходной
окружности гомотетией с коэффициентом 1/3 и центром O.
-
19.11.
-
а) При гомотетии с центром B, переводящей вписанную
окружность во вневписанную окружность, касающуюся стороны AC,
точка M переходит в некоторую точку Mў. Точка Mў является
концом диаметра, перпендикулярного прямой AC, поэтому Mў
является точкой касания вписанной окружности со стороной AC,
а значит, и точкой пересечения прямой BM со стороной AC.
Поэтому K = Mў и точка K является точкой касания вневписанной
окружности со стороной AC. Теперь легко вычислить, что
AK = (a + b – c)/2 = CD, где a, b и c - длины сторон треугольника ABC.
б) Рассмотрим гомотетию с центром M, переводящую прямую EH в
прямую, касающуюся данной окружности. При этой гомотетии
точки E, F, K и H переходят в точки Eў, Fў, Kў и Hў.
Согласно задаче a) EўFў = KўHў, поэтому EF = KH.
-
19.12.
-
Воспользуемся решением и обозначениями задачи 19.11, а).
Так как AK = DC, то B1K = B1D, а значит, B1O - средняя линия
треугольника MKD.
-
19.13.
-
Пусть Oa, Ob, Og и Od - центры окружностей a,
b, g и d; O1 и O2 - центры вписанной и описанной
окружностей треугольника ABC. Треугольник OaObOg
переходит в треугольник ABC при гомотетии с центром O1. При этой
гомотетии точка O2 переходит в центр описанной окружности
треугольника OaObOg, совпадающий с точкой Od.
Поэтому точки O1, O2 и Od лежат на одной прямой.
-
19.14.
-
Пусть A1, B1 и C1 - центры данных окружностей, касающихся
сторон треугольника, O - центр окружности, касающейся
этих окружностей, O1 и O2 - центры вписанной и описанной
окружностей треугольника ABC. Прямые AA1, BB1 и CC1 являются
биссектрисами треугольника ABC, поэтому они пересекаются в точке O1.
Следовательно, треугольник A1B1C1 переходит в треугольник
ABC при гомотетии с центром O1, причем коэффициент гомотетии
равен отношению расстояний от точки O1 до сторон треугольников
ABC и A1B1C1, т. е. равен (r – r)/r. При этой гомотетии
описанная окружность треугольника ABC переходит в описанную окружность
треугольника A1B1C1. Так как OA1 = OB1 = OC1 = 2r, радиус
описанной окружности треугольника A1B1C1 равен 2r.
Следовательно, R(r – r)/r = 2r, т. е. r = rR/(2r + R).
-
19.15.
-
Пусть X - центр гомотетии (с положительным коэффициентом),
переводящей вписанную окружность треугольника ABC в описанную
окружность. Прямая AX пересекает вписанную окружность в точках
Aў и Aўў, одна из которых (для определенности Aўў) при
указанной гомотетии переходит в точку A, а другая - в
некоторую точку A2, лежащую на описанной окружности.
Рассмотрим гомотетию с центром A, переводящую Aў в A2.
При этой гомотетии центр вписанной окружности переходит в точку,
лежащую на отрезке OA2. Это означает, что вписанная
окружность переходит в окружность, касающуюся описанной
окружности в точке A2. Следовательно, A2 = A1. Поэтому
прямые AA1, BB1 и CC1 проходят через точку X.
-
19.16.
-
Возьмем на биссектрисе угла ABC произвольную точку O
и построим окружность S с центром O, касающуюся сторон
угла. Прямая BM пересекает окружность S в точках M1 и M2.
Задача имеет два решения: при гомотетии с центром B, переводящей M1
в M, и при гомотетии с центром B, переводящей M2 в M,
окружность S переходит в окружности, проходящие через точку M
и касающиеся сторон угла.
-
19.17.
-
Ясно, что обе окружности касаются одной из сторон
треугольника. Покажем, как построить окружности, касающиеся
стороны AB. Возьмем прямую cў параллельную прямой AB.
Построим окружности S1ў и S2ў одного радиуса, касающиеся друг
друга и прямой cў. Построим касательные aў и bў к этим окружностям,
параллельные прямым BC и AC соответственно. Треугольник AўBўCў,
образованный прямыми aў, bў и cў, имеет стороны, параллельные
сторонам треугольника ABC. Поэтому существует гомотетия, переводящая
треугольник AўBўCў в треугольник ABC. Искомые окружности являются
óбразами окружностей S1ў и S2ў при этой гомотетии.
-
19.18.
-
а) Отложим на сторонах AB и BC треугольника ABC
отрезки AX1 и CY1 равной длины a. Проведем через точку Y1
прямую l, параллельную стороне AC. Пусть Y2 - точка
пересечения прямой l и окружности радиуса a с центром X1,
лежащая внутри треугольника. Тогда искомая точка Y является точкой
пересечения прямой AY2 со стороной BC, X - такая точка
луча AB, что AX = CY.
б) Возьмем на стороне AB произвольную точку X1 № B. Окружность
радиуса BX1 с центром X1 пересекает луч BC в точках B
и Y1. На прямой BC построим такую точку C1, что Y1C1 = BX1
и точка Y1 лежит между B и C1. При гомотетии с центром B,
переводящей точку C1 в C, точки X1 и Y1 переходят в искомые
точки X и Y.
-
19.19.
-
Возьмем отрезок AD и проведем окружности S1 и S2
с центром A и радиусами AB и AC соответственно. Вершина B
является точкой пересечения окружности S1 с образом окружности S2
при гомотетии с центром D и коэффициентом – DB/DC = – AB/AC.
-
19.20.
-
Возьмем на большей окружности S2 произвольную точку X.
Пусть S2ў - образ окружности S2 при гомотетии с центром X
и коэффициентом 1/3, Y - точка пересечения окружностей S2ў
и S1. Тогда XY - искомая прямая.
-
19.21.
-
Восставим из точек B и C перпендикуляры к прямым AB и AC;
пусть P - точка их пересечения. Тогда точка пересечения
прямых AP и BC - искомая.
-
19.22.
-
Проведем к окружностям S1 и S2 общие внешние касательные l1
и l2. Прямые l1 и l2 пересекаются в точке K,
которая является центром гомотетии H, переводящей окружность S1
в окружность S2. Пусть A1 = H(A). Точки A и K лежат на
прямой, соединяющей центры окружностей, поэтому AA1 - диаметр
окружности S2, т. е. РACA1 = 90° и A1C||AB.
Следовательно, отрезок AB при гомотетии H переходит в A1C.
Поэтому прямая BC проходит через точку K и РADK = 90°.
Точка D лежит на окружности S с диаметром AK. Ясно также, что
точка D лежит внутри угла, образованного прямыми l1 и l2.
Таким образом, геометрическим местом точек D является дуга окружности S,
высекаемая прямыми l1 и l2.
-
19.23.
-
Из условия задачи следует, что отображение f взаимно однозначно.
а) Пусть точка A переходит при отображении f в точку Aў,
а B - в точку Bў. Тогда
|
®
BBў
|
= |
®
BA
|
+ |
®
AAў
|
+ |
®
AўBў
|
= – |
®
AB
|
+ |
®
AAў
|
+ |
®
AB
|
= |
®
AAў
|
|
, т. е.
преобразование f является параллельным переносом.
б) Рассмотрим три точки A, B и C, не лежащие на одной
прямой. Пусть Aў, Bў и Cў - их образы при отображении f.
Прямые AB, BC и CA не могут совпасть с прямыми AўBў, BўCў
и CўAў соответственно, так как в этом случае A = Aў, B = Bў
и C = Cў. Пусть AB № AўBў. Прямые AAў и BBў не параллельны,
поскольку иначе четырехугольник ABBўAў был бы параллелограммом
и
. Пусть O - точка пересечения прямых
AAў и BBў. Треугольники AOB и AўOBў подобны с коэффициентом
подобия k, поэтому
, т. е. O - неподвижная
точка преобразования f. Следовательно,
|
®
Of(X)
|
= |
®
f(O)f(X)
|
= k |
®
OX
|
|
для любой точки X, а это означает, что
преобразование f является гомотетией с коэффициентом k и центром O.
-
19.24.
-
Пусть H = H2°H1, где H1 и H2 - гомотетии с
центрами O1 и O2 и коэффициентами k1 и k2. Введем
обозначения Aў = H1(A), Bў = H1(B), Aўў = H2(Aў), Bўў = H2(Bў).
Тогда
и
,
т. е.
. Из этого с помощью предыдущей
задачи получаем, что преобразование H при k1k2 № 1 является
гомотетией с коэффициентом k1k2, а при k1k2 = 1 - параллельным
переносом.
Остается проверить, что неподвижная точка преобразования H
лежит на прямой, соединяющей центры гомотетий H1 и H2.
Так как
и
,
то
|
®
O2Aўў
|
= k2( |
®
O2O1
|
+ |
®
O1Aў
|
) = k2( |
®
O2O1
|
+ k1 |
®
O1A
|
) = k2 |
®
O2O1
|
+ k1k2 |
®
O1O2
|
+ k1k2 |
®
O2A
|
|
.
Для неподвижной точки X получаем уравнение
|
®
O2X
|
= (k1k2 – k2) |
®
O1O2
|
+ k1k2 |
®
O2X
|
|
, поэтому
,
где l
= (k1k2 – k2)/(1 – k1k2).
-
19.25.
-
Точка A является центром гомотетии, переводящей S1
в S2, точка B - центром гомотетии, переводящей S2 в S3.
Композиция этих гомотетий переводит S1 в S3, причем ее центр
лежит на прямой AB. С другой стороны, центром гомотетии,
переводящей S1 в S3, является точка C. В самом деле, точке
пересечения внешних касательных соответствует гомотетия с положительным
коэффициентом, а композиция гомотетий с положительными коэффициентами
является гомотетией с положительным коэффициентом.
-
19.26.
-
а) Пусть K, L, M - точки пересечения прямых AB и CD,
AP и DQ, BP и CQ. Эти точки являются центрами гомотетий HK,
HL и HM с положительными коэффициентами, переводящих
соответственно отрезок BC в AD, AD в PQ и BC в PQ. Ясно,
что HL°HK = HM. Поэтому точки K, L и M лежат на одной
прямой.
б) Пусть K, L, M - точки пересечения прямых AB и CD, AQ
и DP, BQ и CP. Эти точки являются центрами гомотетий HK,
HL и HM, переводящих соответственно отрезок BC в AD, AD в QP,
BC в QP, коэффициент первой гомотетии положительный, а двух
последних - отрицательный. Ясно, что HL°HK = HM. Поэтому
точки K, L и M лежат на одной прямой.
-
19.27.
-
Так как Р(P1A, AB) = Р(P2A, AB), то ориентированные
угловые величины дуг BP1 и BP2 равны. Поэтому при поворотной
гомотетии с центром B, переводящей S1 в S2, точка P1 переходит
в P2, а прямая P1Q1 переходит в прямую P2Q2.
-
19.28.
-
Так как ориентированные угловые величины дуг AM1
и AM2 равны, то Р(M1B, BA) = Р(M2B, BA), а значит,
точки M1, M2 и B лежат на одной прямой.
-
19.29.
-
Пусть Pi - поворотная гомотетия с центром O, переводящая
окружность Si в Si + 1. Тогда Xi + 1 = Pi(Xi) (см. задачу 19.28).
Остается отметить, что композиция Pn°ј°P2°P1
является поворотной гомотетией с центром O, переводящей S1
в S1, т. е. она является тождественным преобразованием.
-
19.30.
-
Так как РAMB = РNAB и РBAM = РBNA, то
DAMB ~ DNAB, а значит, AN : AB = MA : MB = CN : MB. Кроме того, РABM = 180° – РMAN = РANC. Следовательно, DAMB ~ DACN,
т. е. поворотная гомотетия с центром A, переводящая M в B,
переводит C в N, а значит, она переводит Q в P.
-
19.31.
-
Пусть O1 и O2 - центры данных окружностей, r1 и r2
- их радиусы. Коэффициент k поворотной гомотетии, переводящей S1
в S2, равен r1/r2, а ее центр O лежит на окружности с диаметром
O1O2, и, кроме того, OO1 : OO2 = k = r1/r2. Остается
проверить, что окружность с диаметром O1O2 и ГМТ O таких,
что OO1 : OO2 = k, имеют ровно две общие точки. При k = 1 это
очевидно, а при k № 1 последнее ГМТ описано в решении задачи 7.14:
оно является окружностью, причем одна из ее точек пересечения с
прямой O1O2 лежит внутри отрезка O1O2, а другая - вне его.
-
19.32.
-
Рассмотрим преобразование, переводящее треугольник BHC
в треугольник PHB, т. е. композицию поворота на 90°
относительно точки H и гомотетии с коэффициентом BP : CB
и центром H. Поскольку при этом преобразовании вершины квадрата
переходят в вершины квадрата, а точки C и B переходят в точки B
и P, то точка D переходит в точку Q, т. е. РDHQ = 90°.
-
19.33.
-
Пусть P - поворотная гомотетия, переводящая вектор
в вектор
. Тогда
|
®
AA1
|
+ |
®
BB1
|
+ |
®
CC1
|
= |
®
AC
|
+ P( |
®
CB
|
) + |
®
CB
|
+ P( |
®
BA
|
) + |
®
BA
|
+ P( |
®
AC
|
) = |
®
0
|
|
. Значит, если M - центр масс треугольника ABC,
то
|
®
MA1
|
+ |
®
MB1
|
+ |
®
MC1
|
= ( |
®
MA
|
+ |
®
MB
|
+ |
®
MC
|
) + ( |
®
AA1
|
+ |
®
BB1
|
+ |
®
CC1
|
) = |
®
0
|
|
.
-
19.34.
-
Пусть M - общая середина сторон BC и B1C1,
и
. Пусть, далее,
P - поворотная гомотетия с центром M,
углом поворота 90° и коэффициентом Ц3, переводящая
точку B в A, а B1 - в A1. Тогда
и
|
®
AA1
|
= P(y) – P(x) = P( |
®
BB1
|
)
|
.
Поэтому угол между векторами
и
равен 90° и AA1 : BB1 = Ц3.
-
19.35.
-
Пусть P - поворотная гомотетия, переводящая треугольник
ABC в треугольник A1B1C1. Тогда
|
®
A2B2
|
= |
®
A2O
|
+ |
®
OB2
|
= |
®
A1A
|
+ |
®
BB1
|
= |
®
BA
|
+ |
®
A1B1
|
= – |
®
AB
|
+ P( |
®
AB
|
)
|
. Аналогично и остальные векторы сторон
треугольника ABC переводятся в векторы сторон треугольника
A2B2C2 преобразованием f(a) = – a + P(a).
-
19.36.
-
Исходная карта является прямоугольником K0 на плоскости, меньшая
карта - прямоугольником K1, содержащимся в K0.
Рассмотрим поворотную гомотетию f, отображающую прямоугольник K0
на K1. Пусть Ki + 1 = f(Ki). Так как последовательность Ki
является стягивающейся последовательностью вложенных многоугольников,
существует единственная точка X, принадлежащая всем
прямоугольникам Ki. Докажем, что X - искомая точка, т. е.
f(X) = X. В самом деле, так как точка X принадлежит Ki, то точка
f(X) принадлежит Ki + 1, т. е. точка f(X) также принадлежит
всем прямоугольникам Ki. Поскольку имеется только одна точка,
принадлежащая всем прямоугольникам, то f(X) = X.
-
19.37.
-
Так как произведение коэффициентов поворотных гомотетий P1 и P2
равно 1, их композиция является поворотом (см. задачу 17.36).
Пусть O - центр поворота P2°P1; R = P1(O). Так как
P2°P1(O) = O, то P2(R) = O. Следовательно, по условию
A1O : A1R = A2O : A2R и РOA1R = РOA2R,
т. е. DOA1R ~ DOA2R. Кроме того, OR -
общая сторона этих подобных треугольников, значит,
DOA1R = DOA2R.
Следовательно, OA1 = OA2
и
| Р( |
®
OA1
|
, |
®
OA2
|
) = 2Р( |
®
OA1
|
, |
®
OR
|
) = 2Р( |
®
MA1
|
, |
®
MN
|
)
|
, т. е. O - центр поворота на
угол
, переводящего A1 в A2.
-
19.38.
-
Пусть P1 - поворотная гомотетия с центром B, переводящая A
в M, а P2 - поворотная гомотетия с центром D, переводящая M
в C. Так как произведение коэффициентов этих поворотных
гомотетий равно (BM : BA) · (DC : DM) = 1, то их
композиция P2°P1 является поворотом (переводящим A в C) на
угол
| Р( |
®
AB
|
, |
®
BM
|
) + Р( |
®
DM
|
, |
®
DC
|
) = 2Р( |
®
AB
|
, |
®
BM
|
)
|
.
С другой стороны, центр поворота P2°P1 совпадает с центром
поворота на угол
, переводящего B
в D (см. задачу 19.37).
-
19.39.
-
Легко проверить, что tg XBY = k и
, т. е.
точка Y получается из X поворотной гомотетией с центром B,
углом поворота arctg k и коэффициентом
.
Искомое ГМТ - образ данной полуокружности при этой поворотной гомотетии.
-
19.40.
-
Предположим, что треугольник PXY построен, причем
точки X и Y лежат на сторонах AC и CB соответственно. Нам
известно преобразование, переводящее X в Y, а именно -
поворотная гомотетия с центром P, углом поворота j
= РXPY = РMLN и коэффициентом гомотетии k = PY : PX = LN · LM.
Искомая точка Y является точкой пересечения отрезка BC и образа
отрезка AC при этом преобразовании.
-
19.41.
-
Предположим, что четырехугольник ABCD построен.
Рассмотрим поворотную гомотетию с центром A, переводящую B
в D. Пусть Cў - образ точки C при этой гомотетии. Тогда
РCDCў = РB + РD и DCў = (BC · AD)/AB = bd/a.
Треугольник CDCў можно построить по CD, DCў и РCDCў.
Точка A является точкой пересечения окружности радиуса d с
центром D и геометрического места точек X, для которых
CўX : CX = d : a (это ГМТ - окружность; см. задачу 7.14).
Дальнейшее построение очевидно.
-
19.42.
-
а) Если O - центр поворотной гомотетии, переводящей
отрезок AB в отрезок A1B1, то
|
Р(PA, AO) = Р(PA1, A1O) и Р(PB, BO) = Р(PB1, B1O), (1) |
|
а значит, точка O является точкой пересечения описанных окружностей
треугольников PAA1 и PBB1. Случай, когда эти окружности
имеют единственную общую точку P, очевиден: отрезок AB переходит
в отрезок A1B1 при гомотетии с центром P. Если P и O -
две точки пересечения рассматриваемых окружностей, то из равенств (1)
следует, что DOAB ~ DOA1B1, а значит, O -
центр поворотной гомотетии, переводящей отрезок AB в отрезок A1B1.
б) Достаточно заметить, что точка O является центром поворотной
гомотетии, переводящей отрезок AB в отрезок BC, тогда
и только тогда, когда Р(BA, AO) = Р(CB, BO) и
Р(AB, BO) = Р(BC, CO).
-
19.43.
-
Пусть A1 и B1 - положения точек в один момент, A2
и B2 - положения точек в другой момент. Тогда в качестве точки P
можно взять центр поворотной гомотетии, переводящей отрезок
A1A2 в отрезок B1B2.
-
19.44.
-
Пусть P - точка пересечения прямых l1 и l2. Согласно
задаче 19.42 точка O лежит на описанной окружности S1 треугольника
A1A2P. С другой стороны, OA2 : OA1 = k. Геометрическим местом
точек X, для которых XA2 : XA1 = k, является окружность S2
(задача 7.14). Точка O является точкой пересечения окружностей S1
и S2 (таких точек две).
-
19.45.
-
Пусть O - центр поворотной гомотетии, переводящей
отрезок AB в отрезок A1B1. Тогда DABO ~ DA1B1O, т. е. РAOB = РA1OB1 и
AO : BO = A1O : B1O. Следовательно,
РAOA1 = РBOB1 и AO : A1O = BO : B1O,
т. е. DAA1O ~ DBB1O.
Поэтому точка O является центром поворотной гомотетии, переводящей
отрезок AA1 в отрезок BB1.
-
19.46.
-
Пусть прямые AB и DE пересекаются в точке C, а прямые
BD и AE - в точке F. Центром поворотной гомотетии, переводящей
отрезок AB в отрезок ED, является точка пересечения описанных
окружностей треугольников AEC и BDC, отличная от точки C
(см. задачу 19.42), а центром поворотной гомотетии, переводящей AE
в BD, - точка пересечения описанных окружностей треугольников
ABF и EDF. Согласно задаче 19.45 центры этих поворотных
гомотетий совпадают, т. е. все четыре описанные окружности имеют
общую точку.
-
19.47.
-
Центр O параллелограмма ABCD равноудален от следующих пар
прямых: AQ и AB, AB и CD, CD и DQ, поэтому
QO - биссектриса угла AQD. Пусть a
= РBAO,
b
= РCDO и j
= РAQO = РDQO. Тогда a + b
= РAOD = 360° – a – b – 2j, т. е. a + b + j
= 180°, а значит, DQAO = DQOD.
-
19.48.
-
Решим задачу в несколько более общем виде. Пусть на
окружности S взята точка O, H - поворотная гомотетия
с центром O. Докажем, что тогда все прямые XXў, где X -
точка окружности S и Xў = H(X), пересекаются в одной точке.
Пусть P - точка пересечения прямых X1X1ў и X2X2ў.
Согласно задаче 19.42 точки O, P, X1 и X2 лежат на
одной окружности и точки O, P, X1ў и X2ў тоже лежат на
одной окружности. Следовательно, P - точка пересечения
окружностей S и H(S), т. е. все прямые XXў проходят через
точку пересечения окружностей S и H(S), отличную от точки O.
-
19.49.
-
Пусть O - центр поворотной гомотетии, переводящей
треугольник A1B1C1 в треугольник ABC. Докажем, например, что
описанные окружности треугольников ABC2 и A1B1C2 проходят
через точку O. При рассматриваемой гомотетии отрезок AB переходит
в отрезок A1B1, поэтому точка O совпадает с центром поворотной
гомотетии, переводящей отрезок AA1 в отрезок BB1 (см. задачу 19.45).
Согласно задаче 19.42 центр последней гомотетии является второй
точкой пересечения описанных окружностей треугольников ABC2
и A1B1C2 (или точкой их касания).
-
19.50.
-
Точки A1, A2 и A3 лежат на прямых P2P3, P3P1
и P1P2 (рис. 19.2), поэтому описанные окружности треугольников
A1A2P3, A1A3P2 и A2A3P1 имеют
общую точку V
(см. задачу 2.81, а)), причем точки O3, O2 и O1 лежат на
этих окружностях (см. задачу 19.42). Аналогично описанные
окружности треугольников B1B2P3, B1B3P2 и B2B3P1
имеют общую точку Vў. Пусть U - точка пересечения прямых
P2O2 и P3O3. Докажем, что точка V лежит
на описанной окружности треугольника O2O3U. В самом деле,
Р(O2V, VO3) = Р(VO2, O2P2) + Р(O2P2, P3O3) + Р(P3O3, O3V) = Р(VA1, A1P2) + Р(O2U, UO3) + Р(P3A1, A1V) = Р(O2U, UO3). Аналогичные рассуждения
показывают, что точка Vў лежит на описанной окружности
треугольника O2O3U. В частности, точки O2, O3, V и Vў
лежат на одной окружности. Аналогично точки O1, O2, V и Vў
лежат на одной окружности, а значит, точки V и Vў лежат на
описанной окружности треугольника O1O2O3; точка U тоже лежит
на этой окружности. Аналогично доказывается, что прямые P1O1
и P2O2 пересекаются в точке, лежащей на окружности подобия.
Прямая P2O2 пересекает окружность подобия в точках U и O2,
поэтому прямая P1O1 проходит через точку U.
-
19.51.
-
Пусть P1 - точка пересечения прямых A2B2 и A3B3,
P1ў -
точка пересечения прямых A2C2 и A3C3;
точки P2, P3,
P2ў и P3ў
определяются аналогично. При
поворотной гомотетии, переводящей F1 в F2,
прямые A1B1
и A1C1
переходят в A2B2 и A2C2,
поэтому Р(A1B1, A2B2) = Р(A1C1, A2C2).
Аналогичные рассуждения
показывают, что
DP1P2P3 ~ DP1ўP2ўP3ў.
Центр поворотной гомотетии, переводящей отрезок P2P3 в P2ўP3ў,
лежит на описанной окружности треугольника A1P3P3ў
(см. задачу 19.42). А так как Р(P3A1, A1P3ў) = Р(A1B1, A1C1) = Р(A2B2, A2C2) = Р(P3A2, A2P3ў), то описанная окружность треугольника
A1P3P3ў совпадает с описанной окружностью треугольника A1A2P3.
Аналогичные рассуждения показывают, что центр рассматриваемой
поворотной гомотетии является точкой пересечения описанных
окружностей треугольников A1A2P3, A1A3P2 и A2A3P1;
эта точка лежит на окружности подобия фигур F1, F2 и F3
(задача 19.50, а)).
-
19.52.
-
а) Пусть l1ў, l2ў и l3ў - соответственные прямые
фигур F1, F2 и F3, причем liў||li; эти прямые
образуют треугольник P1P2P3. При поворотной гомотетии с
центром O3, переводящей F1 в F2, прямые l1 и l1ў
переходят в l2 и l2ў, поэтому при гомотетии
с центром O3, переводящей прямую l1 в l1ў, прямая l2
переходит в l2ў. Следовательно, прямая P3O3 проходит через
точку W. Аналогично прямые P1O1 и P2O2 проходят через
точку W, а значит, точка W лежит на окружности подобия
фигур F1, F2 и F3 (см. задачу 19.50, б)).
б) Отношение расстояний от точки O1 до прямых l2ў и l3ў
равно коэффициенту поворотной гомотетии, переводящей F2
в F3, а угол P1 треугольника P1P2P3 равен углу ее
поворота. Поэтому Р(O1P1, P1P2) зависит лишь от фигур F2
и F3. А так как Р(O1W, WJ3) = Р(O1P1, P1P2),
то дуга O1J3 фиксирована (рис. 19.3),
а значит, точка J3 фиксирована. Аналогично доказывается, что
точки J1 и J2 фиксированы.
-
19.53.
-
Воспользуемся обозначениями задачи 19.52. Ясно, что
Р(J1J2, J2J3) = Р(J1W, WJ3) = Р(P3P2, P2P1).
Для других углов треугольников доказательство аналогично.
-
19.54.
-
Докажем, например, что при поворотной гомотетии
с центром O1, переводящей F2 в F3, точка J2 переходит
в J3. В самом деле, Р(J2O1, O1J3) = Р(J2W, WJ3).
Кроме того, прямые J2W и J3W являются соответственными прямыми
фигур F2 и F3, поэтому отношение расстояний от них до
точки O1 равно коэффициенту подобия k1, а значит,
O1J2/O1J3 = k1.
-
19.55.
-
Пусть Oa - точка пересечения окружности, проходящей
через точку B и касающейся прямой AC в точке A, и окружности,
проходящей через точку C и касающейся прямой AB в точке A.
Согласно задаче 19.42, б) точка Oa является центром поворотной
гомотетии, переводящей отрезок BA в отрезок AC. Определив
аналогично точки Ob и Oc и воспользовавшись результатом
задачи 19.50, б), получим, что прямые AOa, BOb и COc
пересекаются в точке, лежащей на окружности подобия S.
С другой стороны, эти прямые пересекаются в точке Лемуана K
(см. задачу 5.142).
Серединные перпендикуляры к сторонам треугольника являются
соответственными прямыми рассматриваемых подобных фигур. Они
пересекаются в точке O, поэтому точка O лежит на окружности
подобия S (см. задачу 19.52, а)); кроме того, эти прямые пересекают
окружность S в постоянных точках A1, B1 и C1
треугольника ABC (см. задачу 19.52, б)). С другой стороны,
прямые, проходящие через точку K параллельно BC, CA и AB,
тоже являются соответственными прямыми рассматриваемых фигур
(см. решение задачи 5.146), поэтому они тоже пересекают окружность S
в точках A1, B1 и C1. Следовательно, OA1^A1K1,
т. е. OK - диаметр окружности S.
-
19.56.
-
Если P - первая точка Брокара треугольника ABC, то
CP, AP и BP - соответственные прямые для подобных фигур,
построенных на отрезках BC, CA и AB. Поэтому точка P лежит
на окружности подобия S (см. задачу 19.52, а)). Аналогично точка Q
лежит на окружности S. Кроме того, прямые CP, AP и BP
пересекают окружность S в постоянных точках A1, B1 и C1
треугольника ABC (см. задачу 19.52, б)). А так как KA1||BC
(см. решение задачи 19.55), то Р(PA1, A1K) = Р(PC, CB) = j, т. е. ИPK = 2j. Аналогично ИKQ = 2j.
Поэтому PQ^KO, а значит, OP = OQ и Р(POQ) = (ИPQ)/2 = 2j.
-
19.57.
-
Точка Лемуана имеет трилинейные координаты (a : b :
c), поэтому прямые, проходящие через точку Лемуана параллельно
сторонам треугольника, являются соответственными прямыми фигур,
построенных на сторонах треугольника ABC. (Имеется в виду, что
коэффициент подобия фигур равен отношению сторон.)
-
19.58.
-
а) Оба утверждения непосредственно следуют из
задачи 5.105, а). Действительно, точка Лемуана K лежит
на описанной окружности треугольника A1B1C1 и KA1|| BC и
т. д.
б) Это следует из задачи 5.105, б).
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:46.

 Глава 19. Задачи для самостоятельного решения |
Глава 19. Задачи для самостоятельного решения | 

 Глава 19. Задачи для самостоятельного решения |
Глава 19. Задачи для самостоятельного решения | 