| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
20.1.
-
Пусть a - наименьший угол треугольника. Тогда a Ј 60°.
Поэтому S = (bcsin a)/2 Ј (sin 60°)/2 = Ц3/4.
-
20.2.
-
Пусть X - произвольная точка, лежащая внутри выпуклого
четырехугольника. Так как РAXB + РBXC + РCXD + РAXD = 360°, то наибольший из этих углов не меньше
90°. Пусть для определенности РAXB і 90°.
Тогда точка X лежит внутри окружности с диаметром AB.
-
20.3.
-
Если самолеты из точек A и B прилетели в точку O, то
AB - наибольшая сторона треугольника AOB, т. е.
РAOB > 60°. Предположим, что в точку O прилетели
самолеты из точек A1, ј, An. Тогда один из углов AiOAj
не превосходит 360°/n. Поэтому 360°/n > 60°,
т. е. n < 6.
-
20.4.
-
По крайней мере семь точек отличны от центра O окружности. Поэтому
наименьший из углов AiOAj, где Ai и Aj - данные
точки, не превосходит 360°/7 < 60°. Если A и B -
точки, соответствующие наименьшему углу, то AB < 1, так как
AO Ј 1, BO Ј 1 и угол AOB не может быть наибольшим углом
треугольника AOB.
-
20.5.
-
Один из углов между шестью отрезками, соединяющими
точку O с центрами кругов, не превосходит 360°/6 = 60°.
Пусть РO1OO2 Ј 60°, где O1 и O2 - центры
кругов радиуса r1 и r2 соответственно. Так как РO1OO2 Ј 60°, этот угол не является наибольшим углом треугольника
O1OO2 поэтому либо O1O2 Ј O1O, либо O1O2 Ј O2O.
Пусть для определенности O1O2 Ј O1O. Так как точка O лежит
внутри кругов, то O1O < r1. Поэтому O1O2 Ј O1O < r1,
т. е. точка O2 лежит внутри круга радиуса r1 с центром O1.
-
20.6.
-
Опустим из точки P перпендикуляры PA1, PB1 и PC1 на
стороны BC, CA и AB и выберем наибольший из углов, образованных
этими перпендикулярами и лучами PA, PB и PC. Пусть для
определенности это будет угол APC1. Тогда РAPC1 і 60°,
поэтому PC1 : AP = cos APC1 Ј cos 60° = 1/2,
т. е. AP і 2PC1. Ясно, что неравенство сохранится, если AP
заменить на наибольшее из чисел AP, BP и CP, а PC1 -
на наименьшее из чисел PA1, PB1 и PC1.
-
20.7.
-
Пусть для определенности a - наименьший угол треугольника ABC;
AD - биссектриса. Одна из сторон AB и AC не превосходит
AD/cos (a/2), так как иначе отрезок BC не проходит через
точку D. Пусть для определенности AB Ј AD/cos (a/2) Ј AD/cos 30° Ј 2/Ц3. Тогда SABC = hc AB/2 Ј lc AB/2 Ј 1/Ц3.
-
20.8.
-
Пусть A и B - те из данных точек, расстояние между
которыми минимально. Тогда внутри окружности с диаметром AB
нет данных точек. Пусть C - та из оставшихся точек, из которой
отрезок AB виден под наибольшим углом. Тогда внутри окружности,
проходящей через точки A, B и C, нет данных течек.
-
20.9.
-
Предположим, что получилась замкнутая ломаная.
Пусть AB - наибольшее звено этой ломаной, а AC и BD —
соседние с ним звенья. Тогда AC < AB, т. е. B - не ближайшая
к A точка, и BD < AB, т. е. A - не ближайшая к B точка.
Поэтому точки A и B не могут быть соединены. Получено
противоречие.
-
20.10.
-
Пусть O - данная точка. Проведем прямые, содержащие
стороны многоугольника, и выберем среди них ту, которая наименее
удалена от точки O. Пусть на этой прямой лежит сторона AB.
Докажем, что основание перпендикуляра, опущенного из точки O на
сторону AB, лежит на самой стороне. Предположим, что основанием
перпендикуляра, опущенного из точки O на прямую AB, является
точка P, лежащая вне отрезка AB. Так как точка O лежит внутри
выпуклого многоугольника, отрезок OP пересекает некоторую сторону
CD в точке Q. Ясно, что OQ < OP, а расстояние от точки O до
прямой CD меньше OQ. Поэтому прямая CD менее удалена от
точки O, чем прямая AB, что противоречит выбору прямой AB.
-
20.11.
-
Пусть BE - наибольшая диагональ пятиугольника ABCDE.
Докажем, что тогда из отрезков BE, EC и BD можно составить
треугольник. Для этого достаточно проверить, что BE < EC + BD.
Пусть O - точка пересечения диагоналей BD и EC. Тогда
BE < BO + OE < BD + EC.
-
20.12.
-
Пусть O1 и O2 - центры гомотетий с коэффициентом k,
переводящих многоугольник M в многоугольники M1 и M2. Тогда
точка многоугольника M, наиболее удаленная от прямой O1O2 не
покрыта многоугольниками M1 и M2.
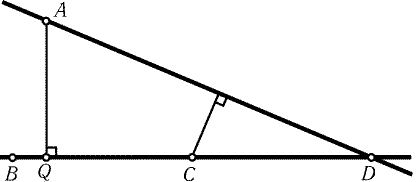
Рис. 20.3
20.13.
Предположим, что не все данные точки лежат на одной
прямой. Проведем через каждую пару данных точек прямую (этих
прямых конечное число) и выберем наименьшее ненулевое расстояние
от данных точек до этих прямых. Пусть наименьшим будет
расстояние от точки A до прямой BC, где точки B и C данные.
На прямой BC лежит еще одна из данных точек - некоторая точка D.
Опустим из точки A перпендикуляр AQ на прямую BC. Две
из точек B, C и D лежат по одну сторону от точки Q,
например C и D. Пусть для определенности CQ < DQ (рис. 20.3).
Тогда расстояние от точки C до прямой AD меньше, чем расстояние
от точки A до прямой BC, что противоречит выбору точки A и
прямой BC.
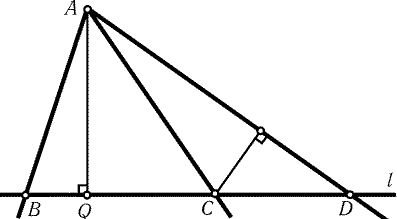
Рис. 20.4
20.14.
Предположим, что не все прямые проходят через одну
точку. Рассмотрим точки пересечения прямых и выберем наименьшее
ненулевое расстояние от этих точек до данных прямых. Пусть
наименьшим будет расстояние от точки A до прямой l. Через
точку A проходят по крайней мере три данные прямые. Пусть они
пересекают прямую l в точках B, C и D. Опустим из точки A
перпендикуляр AQ на прямую l. Две из точек B, C и D лежат
по одну сторону от точки Q, например C и D. Пусть для
определенности CQ < DQ (рис. 20.4). Тогда расстояние от точки C до
прямой AD меньше, чем расстояние от точки A до прямой l, что
противоречит выбору A и l.
-
20.15.
-
Пусть A и B - наиболее удаленные друг от друга данные
точки. Середины отрезков, соединяющих точку A (соответственно
точку B) с остальными точками, все различны и лежат внутри
окружности радиуса AB/2 с центром A (соответственно B).
Полученные два круга имеют лишь одну общую точку, поэтому
различных отмеченных точек не менее 2(n – 1) – 1 = 2n – 3.
-
20.16.
-
Выберем среди всех треугольников с вершинами в данных
точках треугольник наибольшей площади. Пусть это будет
треугольник ABC. Проведем через вершину C прямую lc ||AB.
Если точки X и A лежат по разные стороны от прямой lc,
то SABX > SABC. Поэтому все данные точки лежат по одну
сторону от прямой lc. Аналогично, проводя через точки B и A
прямые lb||AC и la ||BC, получаем, что все данные точки
находятся внутри (или на границе) треугольника, образованного
прямыми la, lb и lc. Площадь этого треугольника ровно
в 4 раза больше площади треугольника ABC, поэтому она не
превосходит 4.
-
20.17.
-
Пусть ABC - треугольник наибольшей площади с вершинами в
вершинах многоугольника M. Тогда многоугольник M содержится
внутри треугольника A1B1C1, серединами сторон которого являются
точки A, B и C. При гомотетии с центром в центре масс
треугольника ABC и коэффициентом – 1/2 треугольник A1B1C1
переходит в треугольник ABC, поэтому многоугольник M переходит
внутрь треугольника ABC.
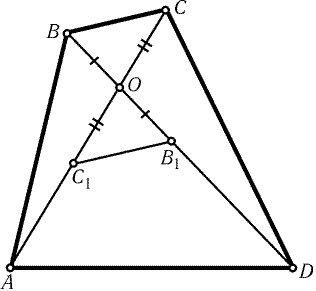
Рис. 20.5
-
20.18.
-
Для определенности можно считать,
что AO і CO и DO і BO.
Пусть точки B1 и C1 симметричны точкам B и C относительно
точки O (рис. 20.5).
Так как треугольник B1OC1 лежит внутри
треугольника AOD, то PAOD і PB1OC1 = PBOC, причем равенство
достигается, только если B1 = D и C1 = A (см. задачу 9.27, б)).
Следовательно, ABCD - параллелограмм. Поэтому AB – BC = PABO – PBCO = 0, т. е. ABCD - ромб.
-
20.19.
-
Пусть O - точка пересечения диагоналей четырехугольника ABCD.
Для определенности можно считать, что
AO і CO и DO і BO.
Пусть точки B1 и C1 симметричны точкам B и C относительно
точки O. Так как точка O является центром вписанной окружности
четырехугольника, то отрезок B1C1 касается этой окружности.
Поэтому отрезок AD может касаться этой окружности, только если
B1 = D и C1 = A, т. е. если ABCD - параллелограмм. В этот
параллелограмм можно вписать окружность, поэтому он - ромб.
-
20.20.
-
Для определенности можно считать, что AO і CO и DO і BO.
Пусть точки B1 и C1 симметричны точкам B и C относительно
точки O. Тогда треугольник C1OB1 содержится внутри треугольника
AOD, поэтому вписанная окружность S треугольника C1OB1
содержится внутри треугольника AOD. Предположим, что отрезок AD
не совпадает с отрезком C1B1. Тогда окружность S переходит во
вписанную окружность треугольника AOD при гомотетии с центром O и
коэффициентом больше 1, т. е. rAOD > rC1OB1 = rCOB.
Получено противоречие, поэтому A = C1 и D = B1, т. е. ABCD -
параллелограмм.
В параллелограмме ABCD площади треугольников AOB и BOC
равны, поэтому если у них равны радиусы вписанных окружностей,
то равны и периметры, так как S = pr. Следовательно, AB = BC,
т. е. ABCD - ромб.
-
20.21.
-
Пусть AB - сторона выпуклой оболочки данных точек,
B1 - ближайшая к A из всех данных точек, лежащих на AB.
Выберем ту из оставшихся точек, из которой отрезок AB1 виден под
наибольшим углом. Пусть это будет точка C. Тогда описанная
окружность треугольника AB1C будет искомой.
-
20.22.
-
Пусть AB - одна из сторон выпуклой оболочки данных
точек. Занумеруем оставшиеся точки в порядке возрастания углов,
под которыми виден из них отрезок AB, т. е. обозначим их через
C1, C2 ј, C2n + 1, так, что РAC1B < РAC2B < ј < AC2n + 1B. Тогда точки C1, ј, Cn лежат вне
описанной окружности треугольника ABCn + 1, а точки Cn + 2, ј, C2n + 1 - внутри ее, т. е. это и есть искомая окружность.
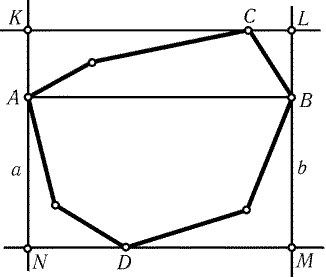
Рис. 20.6
20.23.
Пусть AB - наибольшая диагональ (или сторона) многоугольника.
Проведем через точки A и B прямые a и b, перпендикулярные
прямой AB. Если X - вершина многоугольника, то
AX Ј AB и XB Ј AB, поэтому многоугольник находится внутри полосы,
образованной прямыми a и b. Проведем опорные прямые
многоугольника, параллельные AB. Пусть эти прямые проходят через
вершины C и D и вместе с прямыми a и b образуют прямоугольник
KLMN (рис. 20.6). Тогда SKLMN = 2SABC + 2SABD = 2SACBD. Так
как четырехугольник ACBD содержится в исходном многоугольнике, площадь
которого равна 1, то SKLMN Ј 2.
-
20.24.
-
Выберем наименьшее из всех попарных расстояний между
данными точками и рассмотрим точки, у которых есть соседи на
таком расстоянии. Достаточно доказать требуемое утверждение для
этих точек. Пусть P - вершина их выпуклой оболочки. Если Ai
и Aj - ближайшие к P точки, то AiAj і AiP и
AiAj і AjP, поэтому РAiPAj і 60°.
Следовательно, у точки P не может быть четырех ближайших соседей,
так как иначе один из углов AiPAj был бы меньше 180°/3 = 60°. Поэтому P - искомая точка.
-
20.25.
-
Предположим, что есть картонные квадраты, не совпадающие с
пластмассовыми. Выбросим из рассмотрения все совпадающие квадраты и
рассмотрим выпуклую оболочку вершин оставшихся квадратов. Пусть A -
вершина этой выпуклой оболочки. Тогда A является вершиной двух
разных квадратов - картонного и пластмассового. Легко проверить,
что одна из вершин меньшего из этих квадратов лежит внутри большего
(рис. 20.7). Пусть для определенности вершина B картонного квадрата
лежит внутри пластмассового. Тогда точка B лежит внутри пластмассового
квадрата и является вершиной другого пластмассового квадрата, чего
не может быть. Получено противоречие, поэтому каждый картонный
квадрат совпадает с некоторым пластмассовым.
-
20.26.
-
Рассмотрим выпуклую оболочку данных точек. Возможны два случая.
1. Выпуклая оболочка является параллелограммом ABCD. Если
точка M лежит внутри параллелограмма ABCD, то вершины всех
трех параллелограммов с вершинами A, B и M лежат вне ABCD
(рис. 20.8). Значит, в этом случае, кроме точек A, B, C и D,
никаких других точек быть не может.
2. Выпуклая оболочка не является параллелограммом. Пусть AB
и BC - стороны выпуклой оболочки. Проведем опорные прямые,
параллельные AB и BC. Пусть эти опорные прямые проходят через
вершины P и Q. Тогда вершины всех трех параллелограммов
с вершинами B, P и Q лежат вне выпуклой оболочки (рис. 20.9). Они
даже лежат вне параллелограмма, образованного опорными прямыми,
кроме того случая, когда P и Q являются вершинами этого
параллелограмма. В этом случае его четвертая вершина не принадлежит
выпуклой оболочке, так как та не является параллелограммом.
-
20.27.
-
Возьмем на плоскости произвольную прямую l и спроецируем на нее все
многоугольники. При этом мы получим несколько отрезков, любые два из
которых имеют общую точку. Рассмотрим левые концы этих отрезков и выберем
из них самый правый (чтобы стало ясно, что значит «правый» и «левый»,
на прямой нужно задать направление). Полученная точка принадлежит всем
отрезкам, поэтому проведенный через нее перпендикуляр к прямой l
пересекает все данные многоугольники.
-
20.28.
-
Пусть на плоскости расположено 1000 отрезков. Возьмем
произвольную прямую l, не перпендикулярную ни одному из них,
и спроецируем концы всех этих отрезков на прямую l. Ясно, что
конец отрезка, проецирующийся в самую левую из полученных
точек, не может упираться строго внутрь другого отрезка.
-
20.29.
-
Возможны два варианта расположения четырех точек.
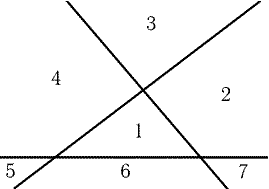
Рис. 20.10
1. Точки являются вершинами выпуклого четырехугольника
ABCD. Выберем наибольший из углов при его вершинах. Пусть
это будет угол ABC. Тогда РABC і 90°, т. е.
треугольник ABC не остроугольный.
2. Точка D лежит внутри треугольника ABC. Выберем наибольший
из углов ADB, BDC и ADC. Пусть это будет угол ADB. Тогда
РADB і 120°, т. е. треугольник ADB тупоугольный.
Доказать, что других вариантов расположения четырех точек
нет, можно следующим образом. Прямые, проходящие через три
из данных точек, делят плоскость на семь частей (рис. 20.10). Если
четвертая данная точка лежит во второй, четвертой или шестой
частях, то имеет место первая ситуация, а если в первой, третьей,
пятой или седьмой, то вторая.
-
20.30.
-
У прямоугольника с вершинами в точках (0, 0), (0, m), (n, 0)
и (n, m) горизонтальная сторона равна n, а вертикальная равна m.
Выберем из данного множества прямоугольник с наименьшей
горизонтальной стороной. Пусть его вертикальная сторона равна m1.
Рассмотрим любые m1 из оставшихся прямоугольников. Возможны два случая.
1. Вертикальные стороны двух из этих m1 прямоугольников
равны. Тогда один из них содержится в другом.
2. Вертикальные стороны всех этих прямоугольников различны. Тогда
вертикальная сторона одного из них больше m1, поэтому он содержит
прямоугольник с наименьшей горизонтальной стороной.
-
20.31.
-
Рассмотрим все окружности, проходящие через две соседние
вершины Ai и Ai + 1 и такую вершину Aj, что
РAiAjAi + 1 < 90°. Хотя бы одна такая окружность есть.
В самом деле, один из углов AiAi + 2Ai + 1 и Ai + 1AiAi + 2
меньше 90°; в первом случае положим Aj = Ai + 2, а во
втором Aj = Ai. Выберем среди всех таких окружностей
(для всех i и j) окружность S наибольшего радиуса; пусть для
определенности она проходит через точки A1, A2 и Ak.
Предположим, что вершина Ap лежит вне окружности S. Тогда
точки Ap и Ak лежат по одну сторону от прямой A1A2
и РA1ApA2 < РA1AkA2 < 90°.
Из теоремы синусов следует, что радиус описанной
окружности у треугольника A1ApA2 больше, чем у треугольника
A1AkA2. Получено противоречие, поэтому окружность S содержит
весь многоугольник A1јAn.
Пусть для определенности РA2A1Ak Ј A1A2Ak. Докажем, что
тогда A2 и Ak - соседние вершины. Если Ak № A3,
то 180° – РA2A3Ak Ј РA2A1Ak < 90°,
поэтому радиус описанной окружности у треугольника A2A3Ak
больше, чем у треугольника A1A2Ak. Получено противоречие,
поэтому окружность S проходит через соседние вершины A1, A2
и A3.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:46.

 Глава 20. § -1 |
Глава 20. § -1 | 

 Глава 20. § -1 |
Глава 20. § -1 | 



