| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
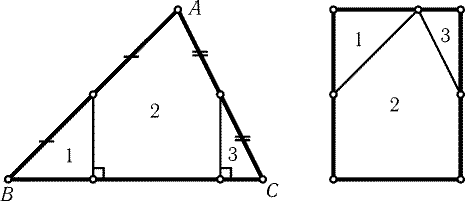
Рис. 25.4
25.1.
Пусть A - наибольший угол треугольника ABC. Тогда углы B
и C острые. Проведя разрезы через середины сторон AB и AC
перпендикулярно BC, переставим полученные части, как показано
на рис. 25.4.
25.2.
Пусть A - наибольший угол треугольника. Разре-
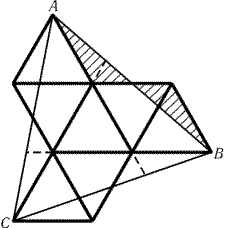
Рис. 25.6
жем треугольник
ABC на равнобедренные треугольники и переставим их, как
показано на рис. 25.5.
25.3.
Сложим 7 одинаковых правильных треугольников, как показано на
рис. 25.6. Тогда ABC - правильный треугольник. Ясно, что
заштрихованные треугольники равны. Теперь легко понять, что на
рис. 25.6 фактически изображено, как разрезать правильный
треугольник ABC шестью прямыми на части, из которых можно
сложить 7 одинаковых правильных треугольников.
25.4.
Требуемые разрезы изображены на рис. 25.7. Отрезок AB равен
стороне квадрата, площадь которого равна площади шестиугольника.
Остальные разрезы проводятся очевидным образом.
25.5.
Мы будем решать обратную задачу: разрежем три квадрата со
стороной a и сложим из них квадрат со стороной Ц3 a.
Требуемые разрезы изображены на рис. 25.8.
25.6.
На рис. 25.9 показано, как это сделать.
25.7.
Нужно доказать, что если есть два прямоугольника со сторонами
a, b и c, d, причем ab = cd = S, то первый прямоугольник можно
разрезать на части и сложить
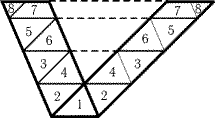
Рис. 25.9
из них второй. Пусть для
определенности a Ј b и c Ј d. Тогда c Ј ЦS Ј b и a Ј d. Отрежем от обоих прямоугольников по два
прямоугольных треугольника с катетами a и c, как показано на
рис. 25.10. Заштрихованные параллелограммы равновелики и имеют
сторону длиной
, поэтому один параллелограмм
можно разрезать на части и сложить из них второй (см. задачу
25.6).
-
25.8.
-
а) Для решения этой задачи нужно воспользоваться результатами
задач 22.23, 25.1 и 25.7. Сначала разрезаем многоугольник
непересекающимися диагоналями на треугольники. Каждый из этих
треугольников разрезаем на части и складываем из них
прямоугольник. Полученные прямоугольники разрезаем на части и
складываем из них прямоугольники со стороной 1. Ясно, что из
нескольких прямоугольников со стороной 1 можно сложить один
прямоугольник со стороной 1.
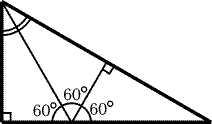
Рис. 25.12
б) Разрежем первый многоугольник на части и сложим из них
прямоугольник со стороной 1. Так как второй многоугольник можно
разрезать на части и сложить из них этот прямоугольник, то и
прямоугольник можно разрезать на части и сложить из них второй
многоугольник (при этом части, на которые был разрезан первый
многоугольник, будут разрезаны на более мелкие части).
-
25.9.
-
Требуемые разрезы изображены на рис. 25.11.
-
25.10.
-
а) Существует. Из трех одинаковых прямоугольных треугольников с
углом 60° можно сложить один прямоугольный треугольник
с углом 60°, как показано на рис. 25.12.
б) Требуемым образом можно разрезать любой прямоугольный
треугольник (рис. 25.13, а ) и треугольник с углами 30°,
30°, 120° (рис. 25.13, б ).
-
25.11.
-
а) Можно считать, что BC/AC = k > 1. Приложим к треугольнику ABC
треугольники 1, 2, 3, 4 и 5 (см. рис. 25.14). Может оказаться, что
треугольники 4 и 5 равны, т. е. k + k3 = k4. В этом случае
дополним конструкцию треугольниками 6 и 7, а треугольник 5
заменим треугольником 8. Тогда треугольники 7 и 8 не равны,
т. е. k6 № k + k3 + k5. В самом деле, так как k + k3 = k4, то
k6 = k2 (k + k3) = k3 + k5 < k + k3 + k5.
б) Предположим, что правильный треугольник разрезан на неравные
правильные треугольники. Стороны двух треугольников разбиения не
могут совпадать. Будем рассматривать только стороны
треугольников разбиения, лежащие внутри (не на границе)
исходного треугольника; пусть N - число таких сторон.
Возникает три
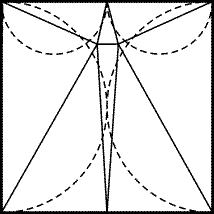
Рис. 25.16
типа вершин треугольников разбиения (см. рис.
25.15). Из каждой вершины 1-го, 2-го и 3-го типа выходит
соответственно 4, 12 и 6 сторон. Пусть n1, n2 и n3 -
количества точек 1-го, 2-го и 3-го типа. Тогда
N = (4n1 + 12n2 + 6n3)/2 = 2n1 + 6n2 + 3n3.
Каждой точке 3-го типа можно сопоставить 3 стороны (на рис. 25.15
это стороны AB, OP и OQ). Легко проверить, что каждая
сторона будет соответствовать хотя бы одной точке 3-го типа.
Следовательно, N Ј 3n3, а значит, 2n1 + 6n2 Ј 0. В
частности, n1 = 0, т. е. разбиение состоит лишь из исходного
треугольника.
25.12.
Требуемые разрезы изображены на рис. 25.16; пунктирные
полуокружности показывают, что все полученные треугольники
остроугольные.
-
25.13.
-
Да, можно. См. рис. 25.17, а ) или рис. 25.17, б ).
-
25.14.
-
РACB > 90° и O - центр вписанной окружности
S треугольника ABC. Проведем к S касательные через точки
пересечения S с отрезками OA и OB и обозначим получившиеся
углы, как показано на рис. 25.18. Последовательно вычисляя углы,
получаем, что j1 = (p – a)/2 < p/2,
j2 = (p – j1)/2 = (p + a)/4 < p/2 (аналогично
j2ў = (p + b)/4),
j3 = p – j2 – g/2 = 3p/4 – a/4 – g/2 < p/2 + (p/4 – g/2) < p/2, j4 = p – 2j2 = (p – a)/2 < p/2 и
j5 = p – j2 – j2ў = p/2 – a/4 – b/4 < p/2.
Аналогично доказывается, что и все остальные углы семи
треугольников, изображенных на рис. 25.18, меньше 90°.
-
25.15.
-
Пусть AB - наибольшая сторона треугольника ABC и AC і BC. Возьмем сначала на стороне AB точку D так, что AD = AC,
затем на BC - точку E так, что BE = BD, затем на AC -
точку F так, что CF = CE, затем на AB - точку G так, что
AG = AF (рис. 25.19). Тогда GD = FC = CE. Пусть O - центр
вписанной окружности треугольника ABC. Так как РCAO = РDAO и CA = DA, то DCAO = DDAO,
поэтому OC = OD. Аналогично OF = OG, OC = OG и OD = OE. Поэтому
OE = OD = OC = OG = OF, т. е. на рис. 25.19 изображено требуемое
разбиение.
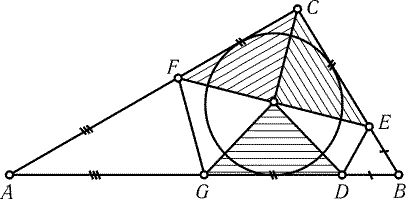
Рис. 25.19
25.16.
Прямая, на которой лежит сторона многоугольника разбиения,
проходит через две вершины исходного многоугольника, а через
каждую вершину исходного многоугольника может проходить не более
двух таких прямых. Поэтому число сторон многоугольника разбиения
не больше числа вершин исходного многоугольника.
25.17.
Если n-угольник разрезан на k треугольников, то каждый его
угол состоит из углов этих треугольников. Поэтому сумма углов
многоугольника не больше суммы углов треугольников, т. е. (n – 2)p Ј k p или n – 2 Ј k.
-
25.18.
-
Сумма внешних углов многоугольника, прилегающих к внутренним
углам, меньшим p, не меньше 2p (см. задачу 22.20).
Внешние углы фигур, на которые распадается оставшаяся часть
листа, являются либо внешними углами квадрата, либо внутренними
углами вырезанных прямоугольников. Поэтому сумма всех внешних
углов этих фигур не превосходит 2p(n + 1), т. е. количество
фигур не превосходит n + 1.
-
25.19.
-
Пусть отрезок MN, где точки M и N лежат на сторонах AB и
CD, разрезает четырехугольник ABCD на два подобных
четырехугольника. Тогда угол AMN четырехугольника AMND равен
одному из углов четырехугольника NMBC. С другой стороны,
РNMB = 180° – РAMN. Поэтому если РAMN = РNMB, то РNMB = 90°, а если угол AMN
равен другому углу четырехугольника NMBC, то в этом
четырехугольнике есть два угла, составляющих в сумме
180°. Проведя аналогичные рассуждения для угла MND,
получаем, что либо AB ^MN и CD ^MN (и тогда AB||CD), либо в четырехугольнике NMBC есть два угла,
составляющие в сумме 180°; без ограничения общности
можно считать, что один из них - угол BMN.
Если РBMN + РMNC = 180°, то BM ||CN.
Если РBMN + РMBC = 180°, то MN ||BC.
Поэтому либо AD ||MN, либо ND ||MA.
Если РBMN + РBCN = 180°, то четырехугольники
NMBC и AMND вписанные. Следовательно, РBCN = 180° – РBMN и РADN = 180° – РAMN = РBMN, т. е. BC ||AD.
-
25.20.
-
Сумма длин границ всех фигур, на которые разбит квадрат, равна
2 · 18 + 4 = 40. В самом деле, проведенные отрезки дают
двукратный вклад в эту сумму, а стороны квадрата однократный.
Пусть для i-й фигуры сумма длин горизонтальных частей границы
равна 2xi, вертикальных 2yi, а ее площадь равна si.
Тогда эту фигуру можно заключить в прямоугольник со сторонами
xi и yi, поэтому xi yi і si, а значит,
| xi + yi і 2 |
Ц
|
xi yi
|
і 2 |
Ц
|
si
|
|
. Следовательно,
| 40 = |
е
| (2xi + 2yi) і 4 |
е
| |
Ц
|
si
|
|
, т. е.
.
Предположим, что si < 0,01 для всех i. Тогда
и
, т. е.
.
Получено противоречие.
-
25.21.
-
Рассмотрим все точки, отличные от вершин исходного треугольника
и являющиеся вершинами полученных треугольников. Пусть m из
этих точек лежит внутри исходного треугольника и n на его
границе. Сумма всех углов полученных треугольников равна
p + pn + 2pm, т. е. число этих треугольников равно
1 + n + 2m. С другой стороны, к внутренней точке прилегает не
более двух углов, превосходящих 120°, а к точке на
границе - не более одного. Поэтому число полученных
треугольников больше, чем число их углов, превосходящих
120°.
-
25.22.
-
Рассмотрим выпуклый многоугольник A1јAn. Докажем,
что каждое из свойств 1 и 2 эквивалентно свойству 3: «Для любого
вектора
найдется вектор
|
®
AjAj + 1
|
= – |
®
AiAi + 1
|
|
.»
Ясно, что из свойства 1 следует свойство 3. Докажем, что из
свойства 3 следует свойство 1. Если выпуклый многоугольник
A1јAn обладает свойством 3, то n = 2m и
|
®
AiAi + 1
|
= – |
®
Am + iAm + i + 1
|
|
. Пусть Oi - середина отрезка
AiAm + i. Так как AiAi + 1Am + iAm + i + 1 -
параллелограмм, то Oi = Oi + 1. Поэтому все точки Oi совпадают,
и эта точка является центром симметрии многоугольника.
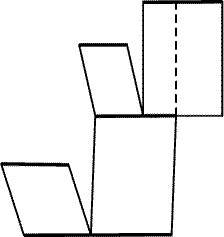
Рис. 25.20
Докажем, что из свойства 2 следует свойство 3. Пусть выпуклый
многоугольник F разрезан на параллелограммы. Нужно доказать, что
для любой стороны многоугольника F найдется другая сторона,
параллельная и равная ей. От каждой стороны многоугольника F
отходит цепочка параллелограммов, т. е. эта сторона как бы
перемещается по ним параллельно, причем она может разбиваться на
несколько частей (рис. 25.20). Так как у выпуклого многоугольника может
быть еще только одна сторона, параллельная данной, то все
разветвления цепочки упираются в одну и ту же сторону, причем ее
длина не меньше длины стороны, из которой цепочка выходит. Мы
можем выпустить цепочку параллелограммов как из первой стороны во
вторую, так и из второй в первую, поэтому длины этих сторон равны.
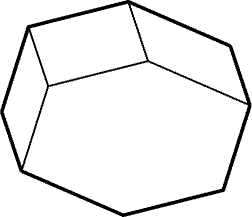
Рис. 25.21
Остается доказать, что из свойства 3 следует свойство 2. Способ
разрезания многоугольника с равными и параллельными противоположными
сторонами указан на рис. 25.21. После каждой такой
операции получаем многоугольник с меньшим числом сторон,
по-прежнему обладающий свойством 3, и проделываем с ним то
же самое, пока не придем к параллелограмму.
25.23.
Воспользуемся результатом предыдущей задачи. Если выпуклый
многоугольник M разрезан на выпуклые центрально симметричные
многоугольники, то их можно разрезать на параллелограммы.
Поэтому M можно разрезать на параллелограммы, т. е. M имеет
центр симметрии.
25.24.
Докажем индукцией по n, что любой 2n-угольник, стороны
которого имеют одну и ту же длину и противоположные стороны
параллельны, можно разрезать на ромбы. Для n = 2 это очевидно,
а из рис. 25.21 ясно, как делается индукционный шаг.
-
25.25.
-
Выделим в правильном восьмиугольнике две взаимно перпендикулярные
пары противоположных сторон и рассмотрим, как и в задаче 25.1,
цепочки параллелограммов, соединяющие противоположные стороны.
На пересечениях этих цепочек стоят прямоугольники. Рассмотрев две
другие пары противоположных сторон, получим еще хотя бы один
прямоугольник.
Параллелограммы каждой цепочки можно дополнительно разрезать так,
чтобы цепочка распалась на несколько «дорожек», причем
в каждой дорожке соседние параллелограммы примыкали бы друг
к другу целыми сторонами, а не частями сторон. Объединение
прямоугольников нового разбиения совпадает с объединением
прямоугольников исходного разбиения, поэтому доказательство достаточно
провести для нового разбиения. Каждая дорожка имеет постоянную
ширину; значит, длина одной стороны каждого прямоугольника,
входящего в дорожку, равна ширине дорожки, а сумма длин всех
других сторон равна сумме всех ширин дорожек, соответствующих
второй паре сторон. Следовательно, площадь всех прямоугольников,
входящих в одну дорожку, равна произведению ширины дорожки
на длину стороны многоугольника, т. е. численно равна ширине
дорожки. Поэтому площадь всех прямоугольников, соответствующих
двум перпендикулярным парам противоположных сторон, равна 1,
а площадь вообще всех прямоугольников равна 2.
-
25.26.
-
Обозначим точки пересечения одной из данных прямых
с остальными через A, B и C. Для определенности будем считать,
что точка B лежит между A и C. Пусть D - точка пересечения
прямых, проходящих через A и C. Любая прямая, проходящая
через точку B и не проходящая через точку D, разрезает треугольник
ACD на треугольник и четырехугольник.
-
25.27.
-
а) Пусть n прямых разбивают плоскость на an частей.
Проведем еще одну прямую. При этом число частей увеличится
на n + 1, так как новая прямая имеет n точек пересечения с уже
проведенными прямыми. Поэтому an + 1 = an + n + 1. Так как a1 = 2,
то an = 2 + 2 + 3 + ј + n = (n2 + n + 2)/2.
б) Заключив все точки пересечения данных прямых в окружность,
легко проверить, что количество неограниченных фигур равно 2n.
Поэтому количество ограниченных фигур равно (n2 + n + 2)/2 – 2n = (n2 – 3n + 2)/2.
-
25.28.
-
а) Все точки пересечения данных прямых можно заключить
в некоторую окружность. Прямые разбивают эту окружность на
4k дуг. Ясно. что две соседние дуги не могут одновременно
принадлежать углам, поэтому число углов не превосходит 2k, причем
равенство может достигаться, только если дуги. принадлежащие
углам, чередуются. Остается доказать, что равенство не может
достигаться. Предположим, что дуги, принадлежащие углам, чередуются.
Так как по обе стороны от любой из данных прямых лежит
по 2k дуг, то противоположные дуги (т. е. дуги, заданные двумя
прямыми) должны принадлежать углам (рис. 25.22), чего не может быть.
б) Для любого n среди полученных фигур может быть три
угла. На рис. 25.23 показано, как построить соответствующее разбиение
плоскости.
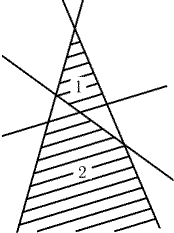
Рис. 25.24
25.29.
Назовем прямую граничной для данной фигуры, если она является
продолжением отрезка или луча, ограничивающего эту фигуру. Достаточно
доказать, что две рассматриваемые фигуры не могут иметь более четырех
общих граничных прямых. Если две фигуры имеют четыре общие граничные
прямые, то одна из фигур лежит в области 1, а другая лежит в области 2
(рис. 25.24). Пятая граничная прямая фигуры, лежащей в области 1, должна
пересекать две соседние стороны четырехугольника 1, но тогда она не
может быть граничной прямой для фигуры, лежащей в области 2.
-
25.30.
-
Рассмотрим все точки пересечения данных прямых. Докажем,
что эти точки могут лежать по одну сторону не более чем от двух данных
прямых. Предположим, что вес точки пересечения лежат по одну сторону
от трех данных прямых. Эти прямые образуют треугольник ABC.
Четвертая прямая не может пересекать только стороны этого
треугольника, т. е. она пересекает хотя бы одно продолжение стороны.
Пусть для определенности она пересекает продолжение стороны AB за
точку B в некоторой точке M. Тогда точки A и M лежат по
разные стороны от прямой BC. Получено противоречие. Поэтому имеются
по крайней мере n – 2 прямые, по обе стороны от которых лежат точки
пересечения.
Если мы выберем в полуплоскости, заданной прямой l, ближайшую к l
точку пересечения, то эта точка будет вершиной треугольника,
прилегающего к прямой l. Таким образом, имеется не менее n – 2
прямых, к которым прилегает по крайней мере по два треугольника,
и две прямые, к каждой из которых прилегает хотя бы один
треугольник. Так как каждый треугольник прилегает ровно к трем
прямым, то треугольников не менее (2(n – 2) + 2)/3.
-
25.31.
-
Если P - точка пересечения данных прямых, то из P выходит
2l(P) отрезков или лучей. Кроме того, каждый из x отрезков
имеет две граничные точки, а каждый из 2n лучей имеет одну
граничную точку. Поэтому
, т. е.
.
-
25.32.
-
Доказательство проведем индукцией по n. Для двух прямых
утверждение очевидно. Предположим, что утверждение верно для
n – 1 прямых, и рассмотрим систему, состоящую из n прямых.
Пусть f - количество частей, на которые данные n прямых
разбивают плоскость;
. Выбросим из данной
системы одну прямую и для полученной системы прямых определим
аналогичным образом числа fў и gў. Если на выброшенной прямой
лежит k точек пересечения прямых, то fў = f – k – 1 и
| gў = 1 + (n – 1) + |
е
| (lў(P) – 1)
|
. Легко проверить, что
|
е
| (l(P) – 1) = – k + |
е
| (lў(P) – 1)
|
. По предположению индукции fў = gў. Поэтому
f = fў + k + 1 = gў + k + 1 = g. Ясно также, что количество неограниченных
частей равно 2n.
-
25.33.
-
Пусть akў - количество красных k-угольников, aў -
количество ограниченных красных областей, количество отрезков, на
которые данные прямые разбиты точками их пересечения, равно
(см. задачу 25.31). Каждый отрезок является стороной
не более чем одного красного многоугольника, поэтому
| 3aў Ј |
е
k і 3
|
kakў Ј |
е
| l(P) – n
|
, причем одно неравенство
достигается тогда и только тогда, когда нет красных k-угольников,
где k > 3, а другое неравенство достигается тогда и только тогда,
когда любой отрезок является стороной красного k-угольника,
т. е. любая неограниченная красная область является углом.
Количество ограниченных областей равно
(см. задачу 25.32). поэтому количество bў ограниченных синих
областей равно
| c – aў і 1 – n + |
е
| (l(P) – 1) – ( |
е
| l(P) – n)/3 = 1 – (2n/3) + |
е
| (2l(P)/3 – 1)
|
. Цвета 2n неограниченных областей чередуются,
поэтому
| b = bў + n і 1 + (n/3) + |
е
| (2l(P)/3 – 1)
|
и
| a = aў + n Ј (2n + |
е
| l(P))/3
|
, а значит,
| 2b – a і 2 + |
е
| (l(P) – 2)
|
.
-
25.34.
-
Можно. Пример изображен на рис. 25.25.
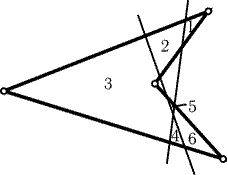
Рис. 25.25
25.35.
Докажем по индукции, что любой выпуклый n-угольник, где n і 5, можно разрезать на пятиугольники. Для n = 5 это очевидно, а
как это сделать для n = 6 и 7, показано на рис. 25.26.
Предположим теперь, что n і 8 и любой выпуклый m-угольник,
где 5 Ј m Ј n, можно разрезать на пятиугольники. От
n-угольника можно отрезать пятиугольник, образованный пятью
последовательными вершинами. При этом остается (n – 3)-угольник.
Так как 5 Ј (n – 3) < n, то (n – 3)-угольник можно разрезать на
пятиугольники по предположению индукции.
-
25.36.
-
Пусть квадрат разрезан на m квадратиков. Разрежем один из этих
квадратиков на 4 квадратика. При этом квадрат будет разрезан на
m + 3 квадратиков. Остается заметить, что квадрат можно
разрезать на 6, 7 и 8 квадратиков (рис. 25.27).
-
25.37.
-
Докажем по индукции, что (3k + 1)-угольник нельзя разрезать по
диагоналям на k пятиугольников. Для k = 1 это утверждение
очевидно. Предположим теперь, что оно доказано для всех
(3k + 1)-угольников, и докажем его для (3k + 4)-угольника.
Предположим, что (3k + 4)-угольник разрезан по диагоналям на
k + 1 пятиугольник. Если каждый из них имеет не более трех
сторон на границе, то число сторон многоугольника не более
3k + 3. Поэтому существует пятиугольник с четырьмя сторонами на
границе. Отрезав его, получим (3k + 1)-угольник, разрезанный
диагоналями на k пятиугольников. Получено противоречие.
-
25.38.
-
Если провести разрезы, близкие к вершинам выпуклого
n-угольника, то можно отсечь от него n треугольников и
получить выпуклый 2n-угольник. Легко проверить, что при этом
любая прямая пересекает не более двух отсеченных треугольников.
Отсечем от правильного треугольника 3 треугольника, затем от
полученного шестиугольника - 6 треугольников и так далее, до
тех пор, пока не получим 3 · 219-угольник. Любая прямая
может пересечь не более двух треугольников, отсекаемых на каждом
шаге. Поэтому всего прямая может пересечь не более 1 + 2 · 19 = 39 многоугольников. Общее число многоугольников, на которые
разбит правильный треугольник, равно 1 + 3 + 3 · 2 + … + 3 · 218 = 1 + 3(219 – 1) > 220 = (210)2 > 10002. Ясно, что
можно отсекать не все треугольники, чтобы получить ровно 1000000
многоугольников.
-
25.39.
-
Ясно, что после n разрезаний получится n + 1 кусок. Так как
после каждого разрезания общее число вершин полученных фигур
увеличивается на 2, 3 или 4, то после n разрезаний общее число
вершин не превосходит 4n + 4. Если после n разрезаний
получилось 100 20-угольников, то кроме 20-угольников есть еще
n + 1 – 100 кусков, так как общее число кусков равно n + 1.
Поскольку у каждого куска не менее трех вершин, общее число
вершин не меньше 100 · 20 + (n – 99) · 3 = 1703 + 3n.
Следовательно, 1703 + 3n Ј 4n + 4, т. е. n і 1699.
Остается доказать, что за 1699 разрезаний можно разрезать
квадрат требуемым образом. Чтобы разрезать квадрат на 100
прямоугольников, достаточно 99 разрезов, а чтобы отрезать от
каждого из этих прямоугольников по 16 треугольников и превратить
их в 20-угольники, достаточно 16000 разрезов.
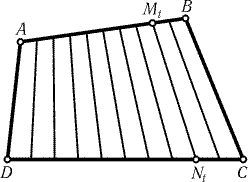
Рис. 25.28
25.40.
Введем систему координат с началом в одной из вершин исходного
прямоугольника и осями, направленными по его сторонам. Разрежем
координатную плоскость прямыми x = n/2 и y = m/2, где m и n
- целые числа, и раскрасим полученные части в шахматном
порядке. Если стороны прямоугольника параллельны осям координат,
а длина одной из его сторон равна 1, то суммы площадей его белых
и черных частей равны. В самом деле, при симметрии относительно
средней линии прямоугольника белые части переходят в черные и
наоборот. Для прямоугольника с целочисленной стороной
справедливо аналогичное утверждение, потому что его можно
разрезать на прямоугольники со стороной 1. Остается доказать,
что если суммы площадей белых и черных частей равны, то одна из
сторон прямоугольника целочисленная. Предположим, что обе
стороны исходного прямоугольника не целые. Прямые x = m и y = n
отрезают от него прямоугольники, одна из сторон каждого из
которых равна 1, и прямоугольник, обе стороны которого меньше 1.
Легко проверить, что в последнем прямоугольнике суммы площадей
белых и черных частей не могут быть равны.
-
25.41.
-
Возьмем на сторонах AB и DC точки Mt и Nt так, что
AMt : Mt B = DNt : Nt C = t : (1 – t), где 0 < t < 1. Тогда
семейство отрезков Mt Nt, а также отрезки AD и BC
образуют искомое разбиение (рис. 25.28).
-
25.42.
-
Возьмем на стороне BC треугольника ABC точку P, а на
стороне AC - точки Q и R. «Вырожденный
четырехугольник» QRCP и четырехугольник AQPB можно разбить
на отрезки, как это делалось в предыдущей задаче (рис. 25.29).
-
25.43.
-
Разделим диаметр AB точками C, D, E и F на 5 равных
частей. Пусть точки Mt и Pt лежат на отрезках CD и EF,
причем CMt : Mt D = FPt : Pt E = t :
: (1 – t), где 0 < t < 1, а
точки Qt и Nt лежат на разных дугах окружности, заданных
точками A и B, и делят эти дуги в отношении t : (1 – t)
(рис. 25.30). Отрезки Mt Nt и Pt Qt вместе с отрезками
AC, DE и FB дают требуемое разбиение.
-
25.44.
-
Разбиение плоскости на отрезки изображено на рис. 25.31.
Выделенные ломаные состоят из концов отрезков разбиения; их
звенья, естественно, не являются отрезками разбиения.

Рис. 25.31
25.45.
Выберем среди всех отрезков, покрывающих левый конец исходного
отрезка, тот, у которого правый конец самый правый, и обозначим
этот отрезок I1. После того как выбран отрезок Ik,
выбираем среди всех отрезков, покрывающих его правый конец, тот,
у которого правый конец самый правый. Таким образом выберем
несколько отрезков, полностью покрывающих исходный отрезок.
Остается доказать, что сумма их длин не превосходит 2. Отрезок
Ik + 2 не имеет общих точек с Ik, так как иначе вместо
Ik + 1 мы должны были бы выбрать Ik + 2. Поэтому каждая
точка исходного отрезка длиной 1 покрыта не более чем двумя
отрезками Ik, т. е. сумма длин этих отрезков не превосходит
2.
-
25.46.
-
Будем последовательно выбрасывать отрезки, покрытые одним или
несколькими оставшимися отрезками, до тех пор, пока это
возможно. Направим ось координат по данному отрезку и обозначим
координаты концов оставшихся отрезков через ak и bk
(ak < bk). Один из двух отрезков с общим левым концом всегда
будет выброшен, поэтому можно считать, что a1 < a2 < a3 < … < an. Докажем, что тогда bk < ak + 2, т. е. четные
отрезки не пересекаются и нечетные тоже. Предположим, что bk і ak + 2. Возможны два случая.
1. bk + 1 Ј bk + 2, тогда отрезок с номером k + 1 покрыт
отрезками с номерами k и k + 2. Получено противоречие.
2. bk + 1 і bk + 2, тогда отрезок с номером k + 2 покрыт
отрезком с номером k + 1. Получено противоречие.
Остается заметить, что сумма длин либо четных, либо нечетных
отрезков не меньше 0,5.
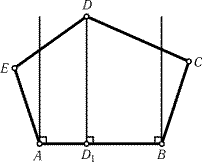
Рис. 25.32
25.47.
Пусть AB - наибольшая сторона пятиугольника. Рассмотрим
полосу, заданную перпендикулярами к стороне AB, проведенными
через A и B. Так как углы EAB и ABC тупые, точки E и
C лежат вне этой полосы. Поэтому точка D лежит внутри
полосы, так как иначе длина одного из отрезков ED и DC была
бы больше длины отрезка AB. Обозначим проекцию точки D на
отрезок AB через D1 (рис. 25.32). Тогда круги с диаметрами
AD и BD полностью покрывают четырехугольники AEDD1 и
BCDD1.
25.48.
а) Рассмотрим наибольший квадрат K покрытия и выбросим все
квадраты, пересекающиеся с ним. Они лежат внутри квадрата,
сторона которого в 3 раза больше стороны K, поэтому площадь,
занимаемая ими, не больше 81, где s - площадь K. Квадрат
K относим к выбранным и в дальнейшем его уже не рассматриваем.
Для остальных квадратов проделываем то же самое до тех пор, пока
все квадраты будут либо выбраны, либо выброшены. Если сумма
площадей выбранных квадратов равна S, то общая площадь
выброшенных квадратов не превосходит 8S. Поэтому 1 Ј S + 8S,
т. е. S і 1/9.
б) Выберем круг наибольшего радиуса, раздуем его в три раза и
выбросим все круги, целиком лежащие в этом раздутии. Оставшиеся
круги не пересекаются с первым. Для них проделаем то же самое и
т. д. Раздутия всех выбранных кругов содержат все данные круги,
а площадь раздутия в 9 раз больше площади исходного круга,
поэтому 9S і 1, где S - общая площадь всех выбранных
кругов. Следовательно, S і 1/9.
-
25.49.
-
Проведем прямую l так, что две данные точки лежат по одну
сторону от нее и две - по другую. Пусть точки A и B лежат
по одну сторону от l, C и D - по другую. Пусть A1 и
B1 - проекции точек A и B на прямую l. Поставим в
точке A прожектор так, чтобы он освещал угол, заданный лучом
AA1 и лучом, параллельным l и пересекающим прямую BB1.
Прожектор в точке B поставим аналогичным образом (рис. 25.33,
а ). Эти два прожектора освещают полуплоскость, содержащую точки
C и D. Аналогично в точках C и D ставим прожекторы,
освещающие другую полуплоскость. (Если AB ^l, то
прожекторы нужно направить так, как показано на рис. 25.33, б .)
-
25.50.
-
а) Не верно. Пусть F - правильный треугольник со стороной
1. Легко проверить, что длина проекции F на любую прямую не
больше 1. С другой стороны, так как треугольник F
остроугольный, его нельзя накрыть кругом, радиус которого меньше
радиуса описанной окружности (см. задачу 9.92). Диаметр
описанной окружности треугольника F равен 2/Ц3 > 1.
б) Верно. Если проекции фигуры F на две взаимно
перпендикулярные прямые равны a и b, то ее можно заключить в
прямоугольник со сторонами a и b. Диаметр описанной
окружности этого прямоугольника равен
. Но
|
Ц
|
a2 + b2
|
Ј |
Ц
|
1 + 1
|
= Ц2 < 1,5
|
.
-
25.51.
-
Построим круги с центрами в данных точках радиуса a = 1/2 + 1/2n.
Ясно, что пересекающиеся круги радиусов R1 и R2 можно
заключить в круг радиуса не более R1 + R2. Будем так делать до
тех пор, пока не получатся непересекающиеся круги. Все данные
точки расположены на расстоянии не меньше a от границ этих
кругов, поэтому их радиусы можно уменьшить на b < a, и при этом
они по-прежнему будут покрывать все данные точки. Если кругов
k штук, то сумма их диаметров не больше n · 2a – k · 2b Ј 2na – 2b. Нам нужно, чтобы выполнялись следующие условия:
2na – 2b < n и 2b > 1. Они выполняются, если a = 1/2 + 1/2n и
b = 1/2 + 1/4n.
-
25.52.
-
Раздуем все монеты в 2 раза, т. е. для каждой из них рассмотрим
круг радиуса 2r с тем же центром. Если центр одной монеты не
принадлежит раздутию второй монеты, то расстояние между их
центрами больше 2r, а значит, эти монеты не пересекаются.
Кроме того, если центр монеты удален от края стола меньше чем на
r, то она лежит внутри стола. Поэтому раздутия монет полностью
покрывают круг радиуса R – r, так как иначе можно было бы
положить монету с центром в непокрытой точке. Следовательно,
4pr2 n і p(R – r)2, т. е. 2 Цn і (R – r)/r.
25.53.
Требуемое замощение изображено на рис. 25.34.
|
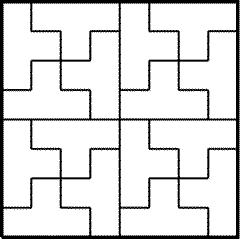 Рис. 25.34
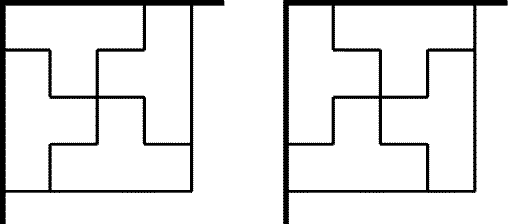 Рис. 25.35
25.54.
Положим первую плитку в углу данного прямоугольника. После этого
замощение квадрата 4 ×4 определяется однозначно (см.
рис. 25.35).
Поэтому данный прямоугольник можно разрезать на квадраты 4 ×4.
 Рис. 25.36
25.55.
а) Докажем это утверждение по индукции. Для квадрата со стороной
2 оно очевидно. Предположим теперь, что можно замостить любой
квадрат со стороной 2n без одной клетки, и покажем, как тогда
замостить квадрат со стороной 2n + 1 без одной клетки.
Разобьем этот квадрат на 4 квадрата со стороной 2n.
Выброшенная клетка попадает в один из них, а по одной клетке в
трех остальных квадратах можно покрыть одной фигуркой (рис.
25.36). Теперь в каждом из этих четырех квадратов со стороной
2n выброшено по одной клетке, поэтому их можно замостить
данными фигурками.
б) Докажем сначала требуемое утверждение для n = 1, т. е. для
квадрата со стороной 7. Можно считать, что выброшенная клетка
лежит в одном из заштрихованных на рис. 25.37 квадратиков;
требуемые замощения изображены на этом же рисунке.
Покажем теперь, как с помощью замощения квадрата со стороной
6n + 1 построить замощение квадрата со стороной 6n + 7. Четыре
квадрата со стороной 6n + 1,
|
прилегающие к вершинам квадрата со
стороной 6n + 7, полностью покрывают этот
квадрат. Поэтому
выброшенная клетка лежит в одном из этих квадратов; замостим
его. Оставшуюся часть можно разрезать на квадраты со стороной
6 и прямоугольники размером 6 ×7. Эти квадраты и
прямоугольники можно разрезать на прямоугольники размером 2×3, каждый из которых состоит из двух плиток.
-
25.56.
-
Требуемое покрытие изображено на рис. 25.38.
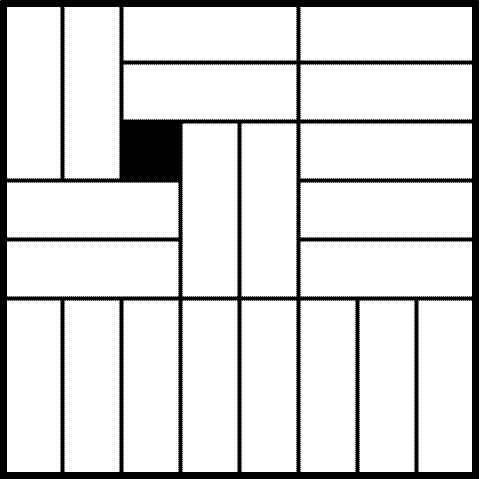
Рис. 25.38
25.57.
Разрежем прямоугольник со сторонами 2n и 2m на квадратики со
стороной 2 и вторым слоем будем мостить каждый квадратик по
отдельности. Квадратик можно замостить либо двумя
горизонтальными костями домино, либо двумя вертикальными. Ясно,
что нам подойдет одно из этих покрытий, так как в квадратике со
стороной 2 не могут содержаться одновременно горизонтальная и
вертикальная кости.
25.58.
Докажем это утверждение для любой фигуры, а не только для
прямоугольника. Возьмем произвольную карточку A0. Одна из ее
клеток покрыта клеткой другой карточки A1, вторая клетка
A1 покрыта клеткой карточки A2 и т. д. Цепочка карточек
A0, A1, A2, … замкнется, причем именно на карточке
A0, так как иначе какая-либо клетка будет покрыта трижды (не
исключено, что эта цепочка состоит только из двух карточек A0
и A1). Замкнутая цепочка карточек состоит из четного числа
карточек (для доказательства можно рассмотреть ломаную, каждое
звено которой соединяет центры клеток одной карточки; эта
ломаная имеет четное число и горизонтальных и вертикальных
звеньев). Поэтому для карточек, входящих в замкнутую цепочку,
искомым разбиением является разбиение на карточки с четными и
нечетными номерами. Все эти карточки выбрасываем и для
оставшихся карточек проделываем такую же операцию и т. д.
-
25.59.
-
а) Нельзя. Предположим, что квадрат 6 ×6 замощен костями
домино 1 ×2 так, что нет «шва». Рассмотрим 10
отрезков, которые делят квадрат на 36 клеток (стороны самого
квадрата мы не рассматриваем). Каждый из этих отрезков разрезает
не менее двух костей. В самом деле, если бы такой отрезок
разрезал одну кость, то по обе стороны от него лежало бы целое
число костей и еще половина кости, т. е. нечетное число клеток.
Этого не может быть, так как площадь каждой из частей, на
которые отрезок разрезает квадрат, четна. Ясно также, что одну
кость не могут разрезать разные отрезки. Поэтому должно быть по
крайней мере 20 костей, а их всего 18.
б) На рис. 25.39 показано, как замостить прямоугольники 5 ×6 и 8 ×8 (при замощении прямоугольника 8 ×8
использовано замощение прямоугольника 5 ×6).
Теперь достаточно доказать, что если можно замостить
прямоугольник m ×n, то можно замостить и прямоугольник
m ×(n + 2). Для этого нужно разрезать замощенный
прямоугольник m ×n на две части, не разрезая костей.
Затем нужно правую часть сдвинуть вправо на расстояние 2 и
промежуток заполнить горизонтальными костями (рис. 25.40).
в) Требуемое замощение изображено на рис. 25.41.
-
25.60.
-
а) Предположим, что круг K радиуса R покрыт паркетом,
состоящим из одинаковых выпуклых n-угольников. Рассмотрим все
точки, лежащие внутри круга K и являющиеся вершинами
n-угольников. Эти точки бывают двух типов: точки 1-го типа
лежат на сторонах других n-угольников и сумма углов,
сходящихся в них, равна 180°; в точках 2-го типа
сходятся углы, сумма которых равна 360°. Пусть p и
q - количества точек 1-го и 2-го типа соответственно. В
каждой точке 1-го типа сходится не менее двух углов
n-угольников, а в каждой точке 2-го типа - не менее трех
углов. Поэтому, 2p + 3q Ј 2n L1, где L1 - количество
n-угольников, пересекающихся с K. Суммы углов, сходящихся в
точках 1-го и 2-го типа равны 180° и 360°
соответственно. Поэтому p + 2q і (n – 2) L2, где L2 -
количество n-угольников, лежащих внутри K. Сложив
неравенства 4p + 6q Ј 4n L1 и – 3p – 6q Ј 6L2 – 3n L2,
получим p Ј 6L2 – n (4L1 – 3L2), т. е. p/L2 Ј 6 – n(4L1/L2 – 3). Так как
, то
. Значит, если из данных выпуклых
n-угольников можно сложить паркет, то 6 – n і 0, т. е. n Ј 6.
б) См. рис. 25.42.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:47.

 Глава 25. § -1 |
Глава 25. § -1 | 

 Глава 25. § -1 |
Глава 25. § -1 | 






