| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
28.1.
-
Пусть R2 - степень инверсии. Тогда OA · OA* = OB · OB* = R2, откуда OA : OB = OB* : OA* и DOAB ~ DOB*A*, поскольку РAOB = РB*OA*.
-
28.2.
-
Опустим из точки O перпендикуляр OC на прямую l
и возьмем произвольную точку M на l. Из подобия треугольников
OCM и OM*C* (задача 28.1) следует, что РOM*C* = РOCM = 90°, т. е. точка M* лежит на окружности S с диаметром OC*.
Если X - какая-то точка S, отличная от O, то она является образом
при инверсии точки Y пересечения прямых l и OX (так как образ
точки Y лежит, с одной стороны, на луче OX, а с другой стороны,
как уже доказано, на окружности S). Итак, инверсия переводит
прямую l в окружность S (без точки O).
-
28.3.
-
Случай, когда окружность S проходит через O, фактически
был разобран в предыдущей задаче (и формально следует из нее,
так как (M*)* = M). Предположим теперь, что точка O не
принадлежит S. Пусть A и B - точки пересечения окружности S
с прямой, проходящей через O и центр S, а M - произвольная
точка S. Докажем, что образом S является окружность с диаметром
A*B*. Для этого достаточно показать, что РA*M*B* = 90°. Но согласно задаче 28.1 DOAM ~ DOM*A* и DOBM ~ DOM*B*,
следовательно, РOMA = РOA*M* и РOMB = РOB*M*,
точнее, Р(OM, MA) = – Р(OA*, M*A*) и Р(OM, MB) = – Р(OB*, M*B*) (чтобы не рассматривать различные случаи
расположения точек, мы воспользуемся свойствами ориентированных углов
между прямыми, изложенными в гл. 2). Поэтому Р(A*M*, M*B*) = Р(A*M*, OA*) + Р(OB*, M*B*) = Р(OM, MA) + Р(MB, OM) = Р(MB, MA) = 90°.
-
28.4.
-
Если точка касания не совпадает с центром инверсии, то
после инверсии эти окружности (окружность и прямая) будут
по-прежнему иметь одну общую точку, т. е. касание сохранится.
Если окружности с центрами A и B касаются в точке O, то
при инверсии с центром O они перейдут в пару прямых,
перпендикулярных AB. Наконец, если прямая l касается в точке O
окружности с центром A, то при инверсии с центром O прямая l
переходит в себя, а окружность - в прямую, перпендикулярную OA.
В каждом из этих случаев получаем пару параллельных прямых.
-
28.5.
-
Проведем через точку пересечения окружностей касательные l1
и l2. Так как при инверсии касающиеся окружности и прямые
переходят в касающиеся (см. задачу 28.4), то угол между образами
окружностей равен углу между образами касательных к ним. При
инверсии с центром O прямая li переходит в себя или в окружность,
касательная к которой в точке O параллельна li. Поэтому угол
между образами прямых l1 и l2 при инверсии с центром O равен
углу между этими прямыми.
-
28.6.
-
Первое решение.
Проведем через центры окружностей координатную ось. Пусть a1
и a2 - координаты точек пересечения оси с S1, b1 и b2
- с S2. Пусть O - точка на оси с координатой x.
Тогда при инверсии с центром O и степенью k наши окружности
перейдут в окружности, диаметры которых лежат на оси, и их
концы имеют координаты a1ў, a2ў и b1ў, b2ў, где
,
,
,
. Полученные окружности
концентричны, если (a1ў + a2ў)/2 = (b1ў + b2ў)/2, т. е.
|
|
1
a1 – x
|
+ |
1
a2 – x
|
= |
1
b1 – x
|
+ |
1
b2 – x
|
, |
|
откуда (b1 + b2 –
a1 – a2)x2
+ 2(a1a2 –
b1b2)x +
b1b2(a1 + a2) –
a1a2(b1 + b2) = 0.
Дискриминант этого квадратного уравнения
относительно x равен 4(b1 – a1)(b1 – a2)(b2 – a1)(b2 – a2).
Он положителен в точности тогда, когда окружности не пересекаются,
что и доказывает существование искомой инверсии.
Существование такой инверсии в случае окружности и прямой
доказывается аналогично.
Второе решение.
Возьмем из прямой, соединяющей центры O1 и O2 окружностей,
точку C так, чтобы касательные, проведенные к окружностям из точки C,
были равны. Эту точку C можно построить, проведя радикальную ось
окружностей (см. задачу 3.54). Пусть l - длина этих касательных.
Окружность S радиуса l с центром в C перпендикулярна S1 и S2.
Поэтому при инверсии с центром O, где O - любая из точек
пересечения окружности S с прямой O1O2, S перейдет в прямую,
перпендикулярную окружностям S1* и S2* и, следовательно,
проходящую через их центры. Но прямая O1O2 тоже проходит через
центры S1* и S2*, поэтому окружности S1* и S2*
концентричны, т. е. O - центр искомой инверсии.
В случае, когда S2 не окружность, а прямая, роль прямой O1O2
играет перпендикуляр, опущенный из точки O1 на S2, точка C
будет точкой его пересечения с S2, а l - длиной касательной,
проведенной из C к S1.
-
28.7.
-
Пусть точка A лежит вне S, тогда Aў лежит внутри S
и РMAўN = (ИMN + ИMўNў)/2 = ИMN = РMON,
т. е. четырехугольник MNOAў вписанный. Но при инверсии относительно S
прямая MN перейдет в окружность, проходящую через точки M, N, O
(задача 28.2). Поэтому точка A* (образ A при инверсии) лежит
на описанной окружности четырехугольника MNOAў. По тем же
причинам точки Aў и A* принадлежат и окружности, проходящей
через Mў, Nў и O. Но эти две окружности не могут иметь других
общих точек, кроме O и Aў.
Следовательно, A* = Aў.
В случае, когда A лежит внутри S, применим уже доказанное
к прямой MNў и точке Aў (она находится вне S). Получим, что
A = (Aў)*. Но тогда Aў = A*.
-
28.8.
-
Пусть точка A лежит вне окружности S. Проведем через A
прямую, касающуюся S в точке M. Пусть MAў — высота
треугольника OMA. Прямоугольные треугольники OMA и OAўM подобны,
поэтому AўO : OM = OM : OA и OAў = R2/OA, т. е.
точка Aў искомая. Если же A находится внутри S, то выполним
построение в обратном порядке: проводим перпендикуляр AM к OA
(точка M лежит на окружности). Тогда касательная к S в точке M
пересекается с лучом OA в искомой точке A*. Доказательство
повторяется дословно.
-
28.9.
-
Если обе данные точки A и B лежат на данной окружности S
(или прямой), то задача решений не имеет. Пусть теперь точка A не
лежит на S. При инверсии с центром A искомая окружность перейдет
в прямую, проходящую через B* и касающуюся S*. Из этого вытекает
следующее построение. Сделаем инверсию относительно произвольной
окружности с центром A. Проведем через B* касательную l к S*.
Еще раз сделаем инверсию. Тогда l перейдет в искомую окружность.
Если точка B* лежит на S*, то задача имеет единственное
решение, если B* лежит вне S*, то решений два, а если внутри,
то ни одного.
-
28.10.
-
После инверсии с центром в данной точке окружности S1
и S2 перейдут в пару окружностей S1* и S2*
(окружность S* и прямую l; пару прямых l1 и l2),
а касающаяся их окружность - в общую касательную к S1*
и S2* (соответственно в касательную к S*, параллельную l;
прямую, параллельную l1 и l2). Поэтому для построения искомой
окружности нужно построить прямую, касающуюся S1* и S2*
(касающуюся S* и параллельную l; параллельную l1 и l2),
и еще раз сделать инверсию.
-
28.11.
-
Сведем эту задачу к задаче 28.10. Пусть окружность S
радиуса r касается окружностей S1, S2, S3 радиусов r1,
r2, r3 соответственно. Касание окружности S с каждой из Si
(i = 1, 2, 3) может быть как внешним, так и внутренним, поэтому
всего возможно восемь различных случаев касания. Пусть, например,
S касается S1 и S3 внешним, а S2 - внутренним образом
(рис. 28.7). Заменим окружности S, S2, S3 на концентрические
им окружности Sў, S2ў, S3ў так, чтобы Sў касалась S2ў
и S3ў и проходила через центр O1 окружности S1. Для этого
достаточно, чтобы радиусы Sў, S2ў, S3ў равнялись r + r1,
r2 + r1, |r3 – r1|. Обратно, по окружности Sў, проходящей
через O1 и касающейся S2ў и S3ў (внешне, если r3 – r1 і 0,
и внутренне, если r3 – r1 < 0), мы можем построить окружность S,
дающую решение задачи, уменьшив радиус Sў на r1. Построение
такой окружности Sў описано в решении задачи 28.10 (если виды
касания заданы, то окружность строится однозначно). Таким же
способом можно выполнить построение и в остальных возможных
вариантах касания.
-
28.12.
-
При инверсии с центром в данной точке A искомая
окружность перейдет в прямую, перпендикулярную образам данных
окружностей S1 и S2, т. е. в прямую, соединяющую центры S1*
и S2*. Таким образом, искомая окружность - образ при этой
инверсии произвольной прямой, проходящей через центры S1* и S2*.
-
28.13.
-
Сделаем инверсию, переводящую окружности S1 и S2
в пару прямых (если они имеют общую точку) или в пару
концентрических окружностей (см. задачу 28.6) с общим центром A.
В последнем случае окружность, перпендикулярная им обеим,
перейдет в прямую, проходящую через A (так как не существует
окружностей, перпендикулярных двум концентрическим окружностям);
касательная, проведенная из A к S*, есть образ искомой
окружности при этой инверсии. Если S1* и S2* -
параллельные прямые, то образ искомой окружности - любая
из двух прямых, перпендикулярных S1* и S2* и касающихся S*.
Наконец, если S1* и S2* - пересекающиеся в некоторой
точке B прямые, то искомая окружность - это образ при инверсии
любой из двух окружностей с центром B, касающихся S*.
-
28.14.
-
После инверсии с центром в точке A задача сводится
к построению прямой l, проходящей через B*, пересекающей
окружность S* под углом a, т. е. к построению точки X на S*
такой, что РB*XO = 90° – a, где O - центр S*.
Эта точка лежит на пересечении S* с дугой, из которой отрезок B*O
виден под углом 90° – a.
-
28.15.
-
а) Пусть AB - данный отрезок. Проведем окружность
с центром B радиуса AB. Отложив на этой окружности хорды AX,
XY и YZ, равные по длине AB, мы получим равносторонние
треугольники ABX, XBY и YBZ. Поэтому РABZ = 180°
и AZ = 2AB.
б) В решении задачи а) описано, как на прямой AB отложить
отрезок BZ, равный AB. Повторив эту процедуру n – 1 раз, получим
отрезок AC, причем AC = n AB.
-
28.16.
-
Проведем окружности с центрами B и C, проходящие
через A. Тогда отличная от A точка пересечения этих окружностей
и будет искомой.
-
28.17.
-
Предположим сначала, что точка A лежит вне окружности S. Пусть B
и C - точки пересечения S и окружности радиуса
AO с центром A. Проведем окружности с центрами B и C радиуса
BO = CO; пусть O и Aў - их точки пересечения. Докажем, что Aў
- искомая точка. Действительно, при симметрии относительно
прямой OA окружности с центрами B и C переходят друг в друга,
поэтому точка Aў остается на месте. Следовательно, точка Aў лежит
на прямой OA. Равнобедренные треугольники OAB и OBAў подобны,
так как имеют равные углы при основании. Следовательно,
OAў : OB = OB : OA или OAў = OB2/OA, что и требовалось.
Пусть теперь точка A лежит внутри S. Будем откладывать
с помощью построения из задачи 28.15, а) на луче OA отрезки
AA2, A2A3, ј, An – 1An, ј длины OA до тех
пор, пока одна из точек An не окажется вне окружности S.
Применив к точке An описанное выше построение, получим на OA
точку An* такую, что OAn* = R2/n OA = OA*/n.
Для того чтобы
построить точку A*, остается только увеличить в n раз
отрезок OAn* (см. задачу 28.15, б)).
-
28.18.
-
Пусть A и B - данные точки. Если точка C лежит на
луче AB и AC = 2AB, то при инверсии относительно окружности
радиуса AB с центром A точка C перейдет в середину отрезка
AB. Построение сведено к задачам 28.15, а) и 28.17.
-
28.19.
-
Центром этой окружности является образ при инверсии
точки Oў, симметричной O относительно AB. Остается применить
задачи 28.16 и 28.17.
-
28.20.
-
Пусть A, B, C - данные точки. Построим (задача 28.17)
образы точек B и C при инверсии с центром A и произвольной
степенью. Тогда окружность, проходящая через A, B и C, будет
образом прямой B*C* при этой инверсии, и ее центр строится по
предыдущей задаче.
-
28.21.
-
а) Пользуясь предыдущей задачей, построим центр O окружности S.
Затем построим точки A* и B* - образы точек A и B при
инверсии относительно S. Образ прямой AB является окружностью S1,
проходящей через точки A*, B* и O. Воспользовавшись
задачей 28.19, построим S1. Искомые точки являются образами точек
пересечения окружностей S и S1, т. е. просто точками
пересечения S и S1.
б) Рассмотрим некоторую инверсию с центром A1. Прямая A2B2
при этой инверсии переходит в окружность S, проходящую через
точки A1, A2* и B2*. Окружность S мы можем построить,
воспользовавшись задачей 28.19. Затем построим точки пересечения S
и прямой A1B1, воспользовавшись решением задачи а). Искомой точкой
является образ точки пересечения, отличной от A1, при
рассматриваемой инверсии.
-
28.22.
-
При инверсии с центром в вершине A сегмента конфигурация,
изображенная на рис. 28.1, перейдет в пару касающихся окружностей,
вписанных в угол с вершиной B*. Ясно, что множество
точек касания таких окружностей - это биссектриса угла, а искомое
множество является ее образом при инверсии - дугой окружности
с концами AB, делящей пополам угол между дугой сегмента
и хордой AB.
28.23.
Пусть C - вершина данного угла. При инверсии с центром
в точке A прямая CB перейдет в окружность S, а окружности S1
и S2 - в окружность S1* с центром O1, касающуюся S
в точке B*, и прямую l, параллельную C*A, касающуюся S1*
в точке X (рис. 28.8). Проведем в окружности S радиус OD^C*A.
Точки O, B* и O1 лежат на одной прямой, a OD||O1X.
Поэтому РOB*D = 90° – РDOB*/2 = 90° – (РXO1B*/2) = РO1B*X, следовательно, точка X
лежит на прямой DB*. Еще раз применив инверсию, получим,
что искомое множество точек касания - это дуга AB окружности,
проходящей через точки A, B и D*.
28.24.
Данная инверсия переводит прямую BC в окружность,
проходящую через точки A, B и C, причем образ отрезка BC
должен остаться внутри угла BAC.
28.25.
Пусть S1 и S2 - окружности, вписанные в сегмент; M, N
- их точки пересечения (рис. 28.9). Покажем, что прямая MN
проходит через точку P окружности сегмента, равноудаленную от его
концов A и B. Действительно, согласно предыдущей задаче инверсия с
центром P и степенью PA2 переводит отрезок AB в дугу AB,
а окружности S1 и S2 - в окружности S1* и S2*,
по-прежнему вписанные в сегмент. Но касательные к S1, проведенные
из P, касаются также и S1*, поэтому S1* = S1 (так как обе
эти окружности одинаковым образом касаются трех фиксированных прямых).
Аналогично S2* = S2, следовательно, точки M и N меняются
местами при инверсии, т. е. M* = N и прямая MN проходит через
центр инверсии.
-
28.26.
-
Сделаем инверсию с центром A. Интересующие нас углы
будут равны тогда (см. задачу 28.5) соответственно углу между прямыми
B*C* и B*D* и углу между прямой C*D* и описанной окружностью
треугольника B*C*D*. Оба этих угла равны половине дуги C*D*.
-
28.27.
-
Сделав инверсию с центром A, мы получим три прямые,
проходящие через B: прямые S1* и S2* касаются
окружности S*, а S3* ей перпендикулярна. Таким образом,
прямая S3* проходит через центр S* и является биссектрисой
угла, образованного S1* и S2*. Следовательно, окружность S3
делит пополам угол между S1 и S2.
-
28.28.
-
Из условия на типы касания следует, что после инверсии
с центром A мы получим две окружности, вписанные в один и тот
же угол или в пару вертикальных углов. В любом случае окружности S1*
и S2* переводятся одна в другую гомотетией с центром A. Эта
гомотетия переводит один отрезок, соединяющий точки касания,
в другой. Поэтому прямые B1*C1* и B2*C2* параллельны,
а их образы при инверсии касаются в точке A.
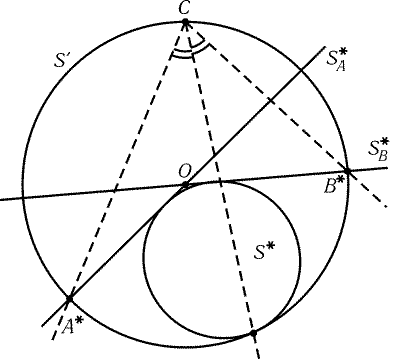
Рис. 28.10
28.29.
Сделаем инверсию с центром C, при которой прямая AB
переходит в окружность Sў, проходящую через точку пересечения
окружностей SA и SB (отличную от точки C). При такой
инверсии окружности SA и SB переходят в прямые, проходящие
через центр O окружности Sў (рис. 28.10). Ясно, что окружность
S* касается окружности Sў в середине дуги A*B*.
28.30.
а) Пусть A1, B1 и C1 - середины сторон BC, CA и AB.
Докажем, например, что описанная окружность треугольника A1B1C1
касается вписанной окружности S и вневписанной окружности Sa,
касающейся стороны BC. Пусть точки Bў и Cў симметричны B
и C относительно биссектрисы угла A (т. е. BўCў - вторая
общая внутренняя касательная к S и Sa), P и Q - точки
касания окружностей S и Sa со стороной BC, D и E -
точки пересечения прямых A1B1 и A1C1 с прямой BўCў.
Согласно задаче 3.2 BQ = CP = p – c, а значит, A1P = A1Q = |b – c|/2.
Достаточно доказать, что при инверсии с центром A1 и
степенью A1P2 точки B1 и C1 переходят в D и E
(при этой инверсии окружности S и Sa переходят в себя,
а описанная окружность треугольника A1B1C1 переходит в
прямую BўCў).
Пусть K - середина отрезка CCў. Точка K лежит на прямой
A1B1, причем A1K = BCў/2 = |b – c|/2 = A1P. Кроме того,
A1D : A1K = BCў : BA = A1K : A1B1, т. е.
A1D · A1B1 = A1K2 = A1P2. Аналогично A1E · A1C1 = A1P2.
б) Окружность Sў, проходящая через середины сторон
треугольника ABC, проходит еще и через основания высот
(задача 5.117). Пусть H - основание высоты, опущенной
из вершины B, B2 - середина стороны AC. Достаточно
проверить, что инверсия с центром A и степенью
| AB2 · AH = |
b
2
|
ccos A = prctg A
|
переводит вневписанную
окружность Sa во вписанную окружность треугольника AB1C1.
Действительно, эта инверсия переводит окружность Sў в себя, а
согласно задаче а) окружности Sў и Sa касаются.
Пусть X - середина отрезка AB1. Тогда CX = r и AX = rctg
A. Остается заметить, что длина касательной из точки A к
окружности Sa равна p.
-
28.31.
-
После инверсии с центром в точке пересечения S1 и S2 получим
прямые l1, l2 и l, пересекающиеся в одной точке. Прямая l1
пересекает окружность S4* в точках A и B, прямая l2
пересекает S3* в точках C и D, а прямая l проходит через
точки пересечения этих окружностей. Поэтому точки A, B, C, D
лежат на одной окружности (задача 3.9).
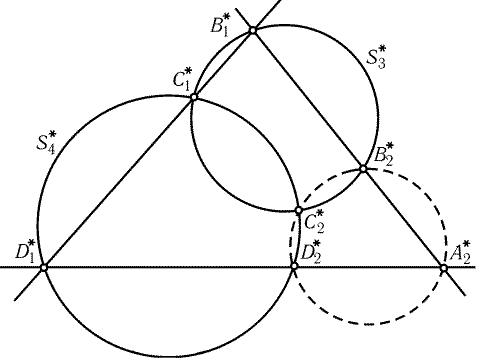
Рис. 28.11
28.32.
Сделаем инверсию с центром в точке A1. Тогда окружности S1,
S2 и S4 перейдут
в прямые A2*D1*,
B1*A2* и
D1*B1*,
окружности S3 и S4 —
в окружности S3* и S4*,
описанные около треугольников B2*C1*B1* и C1*D1*D2*
(рис. 28.11). Проведем окружность через точки B2*, D2*, A2*.
Согласно задаче 2.81, а) она пройдет через точку C2*
пересечения окружностей S3* и S4*. Таким образом, точки A2*,
B2*, C2*, D2* лежат на одной окружности. Следовательно,
точки A2, B2, C2, D2 лежат на одной окружности или прямой.
28.33.
Пусть P, Q, R, S, T - точки пересечения окружностей S1,
S2, S3, S4, S5, о которых говорится в условии (см. рис. 28.4).
Докажем, например, что точки P, Q, R, S лежат на одной
окружности. Проведем окружность S, описанную около треугольника
NKD. Применяя результат задачи 2.85, а) (совпадающей с 19.46) к
четырехугольникам AKDE и BNDC, получаем, что окружности S4,
S5 и S пересекаются в одной точке (в точке P) и
окружности S2, S3, S тоже пересекаются в одной точке (в
точке S). Следовательно, окружность S проходит через точки P
и S. Заметим теперь, что из восьми точек пересечения
окружностей S, S1, S2, S5 четыре, а именно N, A, B,
K лежат на одной прямой. Следовательно, согласно задаче 28.32
оставшиеся четыре точки P, Q, R, S лежат на одной окружности.
-
28.34.
-
После инверсии с центром в точке пересечения описанных
окружностей треугольников A1A2B3, A1B2A3 и B1A2A3
эти окружности перейдут в прямые, а утверждение задачи сведется
к доказательству того, что описанные окружности треугольников
B1*B2*A3*, B1*A2*B3* и A1*B2*B3*
проходят через одну точку, т. е. к утверждению задачи 2.81, а).
-
28.35.
-
После инверсии с центром в точке пересечения описанных
окружностей треугольников A1B1C1, A1B2C2, A2B1C2
и A2B2C1 мы получим четыре прямые и четыре окружности,
описанные около образованных этими прямыми треугольников. Согласно
задаче 2.85, а) эти окружности проходят через одну точку.
-
28.36.
-
а) Обозначим через Mij точку пересечения прямых li и lj,
а через Sij - окружность, соответствующую трем оставшимся
прямым. Тогда точка A1 является отличной от точки M34 точкой
пересечения окружностей S15 и S12.
Повторив это рассуждение для всех точек Ai, получаем, что
они в силу задачи 28.33 лежат на одной окружности.
б) Докажем утверждение задачи по индукции, рассматривая
отдельно случай четного и нечетного n.
Пусть n нечетно. Обозначим через Ai точку, соответствующую
набору из n – 1 прямой, получаемому отбрасыванием прямой li,
а через Aijk - точку, соответствующую набору из n
данных прямых без прямых li, lj и lk. Аналогично
обозначим через Sij и Sijkm окружности, соответствующие
наборам из n – 2 и n – 4 прямых, получаемых отбрасыванием прямых li,
lj и li, lj, lk, lm.
Для того чтобы доказать, что n точек A1, A2, ј, An
лежат на одной окружности, достаточно доказать, что любые четыре из них
лежат на одной окружности. Докажем это, например, для точек A1,
A2, A3 и A4. Так как точки Ai и Aijk лежат на Sij,
то окружности S12 и S23 пересекаются в точках A2
и A123, окружности S23 и S34 - в точках A3
и A234, окружности S34 и S41 - в точках A4
и A134, окружности S41 и S12 - в точках A1
и A124. Но точки A123, A234, A134 и A124
лежат на одной окружности - окружности S1234, поэтому
согласно задаче 28.32 точки A1, A2, A3 и A4 лежат
на одной окружности.
Пусть теперь n четно; Si, Aij, Sijk, Aijkm -
окружности и точки, соответствующие наборам из n – 1, n – 2, n – 3
и n – 4 прямых. Для того чтобы доказать, что окружности S1, S2, ј, Sn пересекаются в одной точке, покажем, что это верно для
любых трех из них. (Этого достаточно при n і 5; см. задачу 26.12.)
Докажем, например, что S1, S2 и S3
пересекаются в одной точке.
По определению точек Aij и окружностей Si и Sijk
точки A12, A13 и A14
лежат на окружности S1;
A12, A23 и A24 - на S2;
A13, A14
и A34 - на S3; A12, A14 и A24 -
на S124; A13, A14, A34 - на S134;
A23, A24, A34 - на S234. Но три
окружности S124, S134 и S234 проходят через
точку A1234 поэтому согласно задаче 28.34
и окружности S1,
S2 и S3 пересекаются в одной точке.
-
28.37.
-
а) Обозначим через Mij точку пересечения прямых li и lj.
Тогда точка A1, соответствующая тройке l2, l3, l4, -
это точка пересечения описанных окружностей треугольников
M2M3M23 и M3M4M34. Рассуждая аналогично для точек A2,
A3 и A4, мы получим, что точки A1, A2, A3 и A4 лежат
на одной окружности согласно задаче 28.32, так как точки M1, M2,
M3, M4 лежат на одной окружности.
б) Как и в задаче 28.36, б), докажем утверждение по индукции,
рассматривая отдельно случаи четного и нечетного n.
Пусть n четно и Ai, Sij, Aijk и Sijkm обозначают
точки и окружности, соответствующие наборам из n – 1, n – 2, n – 3
и n – 4 прямых. Докажем, что точки A1, A2, A3, A4
лежат на одной окружности. По определению точек Ai и Aijk
окружности S12 и S23 пересекаются в точках A2 и A123;
S23 и S34 - в точках A3 и A234; S34 и S41
- в точках A4 и A134; S41 и S12 - в точках A1
и A124. Точки A123, A234, A134 и A124 лежат
на окружности S1234, поэтому согласно задаче 28.32 точки A1,
A2, A3, A4 лежат на одной окружности. Аналогично доказывается,
что и любые четыре из точек Ai (и, следовательно, все они) лежат
на одной окружности.
Доказательство в случае нечетного n і 5 дословно повторяет
доказательство утверждения задачи 28.36, б) для случая четного n.
-
28.38.
-
Если окружности R1 и R2 пересекаются или касаются, то
инверсия с центром в их точке пересечения переведет окружности S1, S2, ј, Sn в окружности, касающиеся пары прямых и друг
друга в точках A1*, A2*, ј, An – 1*, лежащих на
биссектрисе угла, образованного прямыми R1* и R2*, если R1*
и R2* пересекаются, и на прямой, параллельной R1* и R2*,
если эти прямые не пересекаются. Применив инверсию еще
раз, получим, что точки A1*, A2*, ј, An – 1* лежат
на одной окружности.
Если же окружности R1 и R2 не пересекаются, то согласно
задаче 28.6 найдется инверсия, переводящая их в пару концентрических
окружностей. В этом случае точки A1*, A2*, ј, An – 1*
лежат на окружности, концентрической с R1* и R2*, а значит,
точки A1, A2, ј, An – 1 лежат на одной окружности.
-
28.39.
-
Сделаем инверсию, переводящую R1 и R2 в пару
концентрических окружностей. Тогда окружности S1*, S2*, ј, Sn* и T1* равны между собой (рис. 28.12). Повернув цепочку
S1*, ј, Sn* вокруг центра окружности R1* так,
чтобы S1* перешла в T1*, и сделав инверсию еще раз,
получим нужную цепочку T1, T2, ј, Tn.
-
28.40.
-
Центр инверсии, переводящей окружности R1 и R2 в концентрические,
лежит (см. решение задачи 28.6) на линии их центров.
Поэтому, сделав эту инверсию и учтя, что угол между окружностями
и касание при этом сохраняется, мы сведем доказательство к случаю
концентрических окружностей R1 и R2 с центром O и радиусами r1
и r2.
Проведем окружность S с центром P радиуса (r1 – r2)/2,
касающуюся R1 изнутри и R2 внешне,
и две окружности Sў и Sўў
радиуса (r1 + r2)/2 с центрами A и B,
касающиеся R1 и R2
в их точках пересечения с прямой OP (рис. 28.13). Пусть OM и ON
- касательные к S, проведенные из O. Очевидно, что цепочка
из n окружностей, касающихся R1 и R2, существует тогда и
только тогда, когда угол MON равен m 360°/n
(в этом случае окружности цепочки m раз обегают окружность R2).
Поэтому осталось доказать, что угол между окружностями Sў и Sўў
равен РMON. Но угол между Sў и Sўў равен углу между их
радиусами, проведенными в точку пересечения C. Кроме того,
DACO = DPON (так как OP = r1 – (r1 – r2)/2 = (r1 + r2)/2 = AC, PN = (r1 – r2)/2 = r1 – ((r1 + r2)/2) = OA, РPNO = РAOC = 90°). Поэтому РACB = 2РACO = 2РPON = РNOM.
-
28.41.
-
Пусть R1 и R2 - какая¯либо пара несоприкасающихся
окружностей. Оставшиеся четыре окружности образуют цепочку,
поэтому по предыдущей задаче окружности Sў и Sўў, касающиеся R1
и R2 в точках их пересечения с линией центров, пересекаются под
прямым углом (рис. 28.14). Если R2 лежит внутри R1, то радиусы rў
и rўў окружностей Sў и Sўў равны (r1 + r2 + d)/2 и
(r1 + r2 – d)/2, а расстояние между их центрами dў = 2r1 – r1 – r2 = r1 – r2. Угол между Sў и Sўў равен углу между их радиусами,
проведенными в точку пересечения, поэтому (dў)2 = (rў)2 + (rўў)2 или,
после преобразований, d2 = r12 + r22 – 6r1r2.
В случае, когда R1 и R2 не лежат одна внутри другой, радиусы
окружностей Sў и Sўў равны (d + (r1 – r2))/2 и (d – (r1 – r2))/2,
а расстояние между центрами dў = r1 + r2 + d – (r1ў + r2ў) = r1 + r2.
В результате получаем d2 = r12 + r22 + 6r1r2.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:47.

 Глава 28. § -1 |
Глава 28. § -1 | 

 Глава 28. § -1 |
Глава 28. § -1 | 

