| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
5.1.
-
Пусть AC1 = AB1 = x, BA1 = BC1 = y и CA1 = CB1 = z.
Тогда a = y + z, b = z + x и c = x + y. Вычитая третье равенство
из суммы первых двух, получаем z = (a + b – c)/2. Поэтому, если
треугольник ABC задан, то положение точек A1 и B1 определено
однозначно. Аналогично положение точки C1 определено однозначно.
Остается заметить, что точки касания вписанной окружности со сторонами
удовлетворяют указанным в условии задачи соотношениям.
-
5.2.
-
Лучи COa и COb- биссектрисы внешних углов при
вершине C, поэтому C лежит на прямой OaOb и РOaCB = РObCA. Так как COc- биссектриса угла BCA,
то РBCOc = РACOc. Складывая эти равенства,
получаем РOaCOc = РOcCOb, т. е. OcC — высота
треугольника OaObOc. Аналогично доказывается, что OaA и ObB
- высоты этого треугольника.
-
5.3.
-
Ясно, что РBOC = 180° – РCBO – РBCO = 180° – РB/2 – РC/2 = 90° + РA/2,
a РBOaC = 180° – РBOC, так
как РOBOa = РOCOa = 90°.
-
5.4.
-
Пусть AA1,BB1 и CC1- биссектрисы
треугольника ABC, O — точка их пересечения. Предположим,
что x > 1. Тогда РPAB > РPAC, т. е. точка P лежит внутри
треугольника AA1C. Аналогично точка P лежит внутри
треугольников CC1B и BB1A. Но единственной общей точкой трех
этих треугольников является точка O. Получено противоречие.
Случай x < 1 разбирается аналогично.
-
5.5.
-
Пусть da,db и dc- расстояния от точки O до
сторон BC,CA и AB. Тогда ada + bdb + cdc = 2S и aha = bhb = chc = 2S.
Если ha – da = hb – db = hc – dc = x,
то (a + b + c)x = a(ha – da) + b(hb – db) + c(hc – dc) = 6S – 2S = 4S.
Поэтому x = 4S/2p = 2r.
-
5.6.
-
Докажем, что точка O является центром вневписанной
окружности треугольника PBQ, касающейся стороны PQ. В самом
деле, РPOQ = РA = 90° – РB/2; из центра
вневписанной окружности отрезок PQ виден под таким же углом
(задача 5.3). Кроме того, точка O лежит на биссектрисе угла B.
Следовательно, полупериметр треугольника PBQ равен длине проекции
отрезка OB на прямую CB.
-
5.7.
-
Пусть P — точка касания вписанной окружности со
стороной BC, PQ — диаметр вписанной окружности, R — точка
пересечения прямых AQ и BC. Так как CR = BP (см. задачу 19.11, а)) и
M — середина стороны BC, то RM = PM. Кроме того, O —
середина диаметра PQ, поэтому MO||QR, а так как AH||PQ,
то AE = OQ.
-
5.8.
-
Данная окружность может быть как вписанной, так и
вневписанной окружностью треугольника ABC, отсекаемого касательной
от угла. Используя результат задачи 3.2, в обоих случаях
легко проверить, что uv/w2 = (p – b)(p – c)sin Bsin C/ha2. Остается
заметить, что ha = bsin C = csin B и (p – b)(p – c)/bc = sin 2(A/2)
(задача 12.13).
-
5.9.
-
а) Пусть x1 = BP и x2 = AP. Тогда
,
,
| r = |
(x1 + x2)h
a + b + p + x1 + x2
|
|
.
После несложных преобразований требуемое равенство приводится к виду
x2(p2 + x12 – a2) + x1(p2 + x22 – b2) = 0.
Остается заметить, что p2 + x12 – a2 = 2px1cos BPC,
p2 + x22 – b2 = 2px2cos APC и cos BPC = – cos APC.
б) Согласно задаче а)
| rk + 1 = r1 + rk – |
2r1rk
h
|
,
|
где h - расстояние от точки B до прямой A1A2.
-
5.10.
-
Пусть A1,B1 и C1- точки, симметричные точке H
относительно сторон BC,CA и AB соответственно. Так как AB^CH
и BC^AH, то Р(AB,BC) = Р(CH,HA), а так как
треугольник AC1H равнобедренный,
то Р(CH,HA) = Р(AC1,C1C). Следовательно,
Р(AB,BC) = Р(AC1,C1C), т. е. точка C1 лежит на
описанной окружности треугольника ABC. Аналогично доказывается, что
точки A1 и B1 лежат на этой окружности.
-
5.11.
-
Точки X, Y и Z лежат на одной прямой (задача 5.95, а)). Поэтому
SPYZ = SPXZ + SPXY. Кроме того,
, так как PX^BC и PZ^CA.
Подставив аналогичным образом две другие площади, получим
|
|
sin a
PX
|
= |
sin b
PY
|
+ |
sin g
PZ
|
. |
|
Остается заметить, что sin a : sin b : sin g = BC : CA : AB.
-
5.12.
-
а) Пусть M — точка пересечения прямой AI с
описанной окружностью. Проведя через точку I диаметр,
получим AI · IM = (R + d)(R – d) = R2 – d2. Так как IM = CM
(задача 2.4, а)), то R2 – d2 = AI · CM. Остается заметить,
что AI = r/sin (A/2) и CM = 2Rsin (A/2).
б) Пусть M — точка пересечения прямой AIa с описанной
окружностью. Тогда AIa · IaM = da2 – R2. Так как IaM = CM
(задача 2.4, а)), то da2 – R2 = AIa · CM. Остается заметить,
что AIa = ra/sin (A/2) и CM = 2Rsin (A/2).
-
5.13.
-
а) Так как B1- центр описанной окружности
треугольника AMC (см. задачу 2.4, а)), то AM = 2MB1sin ACM. Ясно
также, что MC = r/sin ACM. Поэтому MA · MC/MB1 = 2r.
б) Так как
РMBC1 = РBMC1 = 180° – РBMC и РBC1M = РA,
то
|
|
MC1
BC
|
= |
BM
BC
|
· |
MC1
BM
|
= |
sin BCM
sin BMC
|
· |
sin MBC1
sin BC1M
|
= |
sin BCM
sin A
|
. |
|
Кроме того, MB = 2MA1sin BCM. Поэтому MC1 · MA1/MB = BC/2sin A = R.
-
5.14.
-
Пусть M — середина стороны AC, N — точка
касания вписанной окружности со стороной BC. Тогда BN = p – b (см.
задачу 3.2), поэтому BN = AM, так как p = 3b/2 по условию. Кроме того,
РOBN = РB1AM, а значит, DOBN = DB1AM,
т. е. OB = B1A. Но B1A = B1O (см. задачу 2.4, а)).
-
5.15.
-
Пусть O и O1- центры вписанной и описанной
окружностей треугольника ABC. Рассмотрим окружность радиуса d = OO1
с центром O. Проведем в этой окружности хорды O1M и O1N,
параллельные сторонам AB и AC соответственно. Пусть K — точка
касания вписанной окружности со стороной AB, L — середина
стороны AB. Так как OK^AB, O1L^AB и O1M||AB,
то O1M = 2KL = 2BL – 2BK = c – (a + c – b) = b – a = AE. Аналогично O1N = AD, а
значит, DMO1N = DEAD. Следовательно, радиус
описанной окружности треугольника EAD равен d.
-
5.16.
-
Пусть вписанная окружность касается стороны AC в
точке K, а вневписанная окружность касается продолжения стороны AC
в точке L. Тогда r = CK и rc = CL. Остается воспользоваться
результатом задачи 3.2.
-
5.17.
-
Так как AB/2 = AM = BM, то CM = AB/2 тогда и только
тогда, когда точка C лежит на окружности с диаметром AB.
-
5.18.
-
Пусть M и N — середины сторон AB и CD.
Треугольник APB прямоугольный, поэтому PM = AB/2 и РMPA = РPAM, а значит, PM||AD. Аналогичные рассуждения
показывают, что точки P,M,N и Q лежат на одной прямой
и PQ = PM + MN + NQ = (AB + (BC + AD) + CD)/2.
-
5.19.
-
Пусть F — точка пересечения прямых DE и BC;
K — середина отрезка EC. Отрезок CD является биссектрисой и
высотой треугольника ECF, поэтому ED = DF, а значит, DK||FC.
Медиана DK прямоугольного треугольника EDC в два раза меньше его
гипотенузы EC (задача 5.17), поэтому AD = DK = EC/2.
-
5.20.
-
Прямая EM проходит через середину стороны AB, поэтому она
проходит через середину O отрезка DK. Кроме того, РEKO = РABK = РKBC = РKEO. Поэтому OE = OK = OD.
Согласно задаче 5.17 РDEK = 90°.
-
5.21.
-
Пусть сумма углов при основании AD трапеции ABCD
равна 90°. Обозначим точку пересечения прямых AB и CD
через O. Точка O лежит на прямой, проходящей через середины
оснований. Проведем через точку C прямую CK, параллельную этой
прямой, и прямую CE, параллельную прямой AB (точки K и E лежат
на основании AD). Тогда CK — медиана прямоугольного
треугольника ECD, поэтому CK = ED/2 = (AD – BC)/2 (см. задачу 5.17).
-
5.22.
-
Ясно, что РCEB = РA + РACE = РBCK + РKCE = РBCE.
-
5.23.
-
Отрезки CF и DK являются биссектрисами подобных
треугольников ACB и CDB, поэтому AB : FB = CB : KB.
Следовательно, FK||AC. Аналогично доказывается, что LF||CB.
Поэтому CLFK — прямоугольник, у которого диагональ CF является
биссектрисой угла LCK, т. е. он квадрат.
-
5.24.
-
Так как
,
то
|
sin a
a
|
= |
sin (180° – a – 90° – j)
acos j
|
= |
cos (a + j)
acos j
|
|
,
где a — сторона квадрата ABPQ, j
= РCAB.
Поэтому ctg a
= 1 + tg j.
Аналогично ctg g
= 1 + tg (90° – j) = 1 + ctg j. Следовательно,
| tg a + tg g
= |
1
1 + tg j
|
+ |
1
1 + ctg j
|
= 1
|
, а значит,
cos acos g
= cos asin g + cos gsin a
= sin (a + g) = cos b.
-
5.25.
-
По теореме Пифагора
AP2 + BQ2 + CR2 = (AM2 – PM2) + (BM2 – QM2) + (CM2 – RM2) и
PB2 + QC2 + RA2 = (BM2 – PM2) + (CM2 – QM2) + (AM2 – RM2).
Эти выражения равны.
Так как AP2 + BQ2 + CR2 = (a – PB)2 + (a – QC)2 + (a – RA)2 = 3a2 – 2a(PB + QC + RA) + PB2 + QC2 + RA2,
где a = AB, то PB + QC + RA = 3a/2.
-
5.26.
-
Пусть точка F делит отрезок BC в
отношении CF : FB = 1 : 2; P и Q — точки пересечения
отрезка AF с BD и CE соответственно. Ясно, что треугольник OPQ
правильный. Используя результат задачи 1.3, легко проверить,
что AP : PF = 3 : 4 и AQ : QF = 6 : 1.
Следовательно, AP : PQ : QF = 3 : 3 : 1, а значит,
AP = PQ = OP.
Поэтому РAOP = (180° – РAPO)/2 = 30°
и РAOC = РAOP + РPOQ = 90°.
-
5.27.
-
Пусть A и B, C и D, E и F — точки
пересечения окружности со сторонами PQ,QR,RP треугольника PQR.
Рассмотрим медиану PS. Она соединяет середины параллельных хорд FA
и DC и поэтому перпендикулярна им. Следовательно, PS является
высотой треугольника PQR, а значит PQ = PR. Аналогично PQ = QR.
-
5.28.
-
Пусть H — точка пересечения высот AA1,BB1
и CC1 треугольника ABC. По условию A1H · BH = B1H · AH. С
другой стороны, так как точки A1 и B1 лежат на окружности с
диаметром AB, то AH · A1H = BH · B1H. Следовательно, AH = BH
и A1H = B1H, а значит, AC = BC. Аналогично BC = AC.
-
5.29.
-
а) Предположим, что треугольник ABC неправильный;
например a № b. Так как a + ha = a + bsin g и b + hb = b + asin g,
то (a – b)(1 – sin g) = 0. Поэтому sin g
= 0, т. е. g
= 90°.
Но тогда a № c, и аналогичные рассуждения показывают,
что b
= 90°. Получено противоречие.
б) Обозначим сторону квадрата, две вершины которого лежат
на стороне BC, через x. Из подобия треугольников ABC и APQ,
где P и Q — вершины квадрата, лежащие на AB и AC,
получаем
,
т. е.
. Аналогичные рассуждения
для других квадратов показывают, что a + ha = b + hb = c + hc.
-
5.30.
-
Если a,b и g- углы треугольника ABC, то
углы треугольника A1B1C1 равны (b + g)/2, (g + a)/2
и (a + b)/2. Пусть для определенности a і b і g.
Тогда (a + b)/2 і (a + g)/2 і (b + g)/2.
Следовательно, a
= (a + b)/2 и g
= (b + g)/2,
т. е. a
= b и b
= g.
-
5.31.
-
В любом треугольнике высота больше диаметра вписанной
окружности. Поэтому длины высот- целые числа, бóльшие 2, т. е.
все они не меньше 3. Пусть S — площадь треугольника, a —
наибольшая его сторона, h — соответствующая высота.
Предположим, что треугольник неправильный. Тогда его периметр P
меньше 3a. Поэтому 3a > P = Pr = 2S = ha, т. е. h < 3. Получено
противоречие.
-
5.32.
-
Так как внешний угол при вершине A треугольника ABA1
равен 120° и РA1AB1 = 60°, то AB1-
биссектриса этого внешнего угла. Кроме того, BB1- биссектриса
внутреннего угла при вершине B, поэтому A1B1- биссектриса
угла AA1C. Аналогично A1C1- биссектриса угла AA1B.
Поэтому РB1A1C1 = (РAA1C + РAA1B)/2 = 90°.
-
5.33.
-
Согласно решению предыдущей задачи луч A1C1 является
биссектрисой угла AA1B. Пусть K — точка пересечения биссектрис
треугольника A1AB. Тогда РC1KO = РA1KB = 90° + РA/2 = 120°. Поэтому РC1KO + РC1AO = 180°, т. е. четырехугольник AOKC1 вписанный.
Следовательно, РA1C1O = РKC1O = РKAO = 30°.
-
5.34.
-
а) Пусть S — описанная окружность
треугольника ABC, S1- окружность, симметричная S
относительно прямой BC. Ортоцентр H треугольника ABC лежит на
окружности S1 (задача 5.10), поэтому достаточно проверить, что
центр O окружности S тоже принадлежит S1 и биссектриса внешнего
угла A проходит через центр окружности S1. Тогда POAH — ромб,
так как PO||HA.
Пусть PQ — диаметр окружности S, перпендикулярный прямой BC,
причем точки P и A лежат по одну сторону от прямой BC. Тогда AQ
- биссектриса угла A, а AP — биссектриса внешнего угла A.
Так как РBPC = 120° = РBOC, то точка P является
центром окружности S1, а точка O принадлежит окружности S1.
б) Пусть S — описанная окружность треугольника ABC, Q —
точка пересечения биссектрисы угла BAC с окружностью S. Легко
проверить, что Q — центр окружности S1, симметричной
окружности S относительно прямой BC. Кроме того, точки O и H
лежат на окружности S1, а так как РBIC = 120° и РBIaC = 60° (см. задачу 5.3), то IIa- диаметр
окружности S1. Ясно также, что РOQI = РQAH = РAQH,
так как OQ||AH и HA = QO = QH. Поэтому точки O и H симметричны
относительно прямой IIa.
-
5.35.
-
Построим внешним образом на стороне AC
треугольника ABC правильный треугольник AB1C. Так как РA = 120°, точка A лежит на отрезке BB1. Поэтому BB1 = b + c
и, кроме того, BC = a и B1C = b, т. е. треугольник BB1C искомый.
-
5.36.
-
а) Пусть M1 и N1- середины отрезков BH
и CH, BB1 и CC1- высоты. Прямоугольные
треугольники ABB1 и BHC1- имеют общий острый угол при
вершине B, поэтому РC1HB = РA = 60°. Так как
треугольник BMH равнобедренный, РBHM = РHBM = 30°.
Следовательно, РC1HM = 60° – 30° = 30° = РBHM, т. е. точка M лежит на биссектрисе угла C1HB. Аналогично
точка N лежит на биссектрисе угла B1HC.
б) Воспользуемся обозначениями предыдущей задачи, и пусть, кроме того,
Bў и Cў- середины сторон AC и AB. Так как AC1 = ACcos A = AC/2, то C1Cў = |AB – AC|/2. Аналогично B1Bў = |AB – AC|/2,
т. е. B1Bў = C1Cў. Следовательно, параллельные прямые BB1
и BўO, CC1 и CўO образуют не просто параллелограмм, а ромб.
Поэтому его диагональ HO является биссектрисой угла при вершине H.
-
5.37.
-
Так как РBB1C = РB1BA + РB1AB > РB1BA = РB1BC, то BC > B1C. Поэтому точка K,
симметричная B1 относительно биссектрисы CC1, лежит на
стороне BC, а не на ее продолжении. Так как РCC1B = 30°, то РB1C1K = 60°, а значит,
треугольник B1C1K правильный. В треугольниках BC1B1 и BKB1
сторона BB1 общая, стороны C1B1 и KB1 равны, равны также и
углы C1BB1 и KBB1 но это углы не между равными сторонами. Поэтому
возможны два случая:
1. DBC1B1 = DBKB1. Тогда РBB1C1 = РBB1K = 60°/2 = 30°. Следовательно, если O — точка
пересечения биссектрис BB1 и CC1, то РBOC = РB1OC1 = 180° – РOC1B1 – РOB1C1 = 120°. С
другой стороны, РBOC = 90° + РA/2 (см. задачу 5.3),
т. е. РA = 60°.
2. РBC1B1 + РBKB1 = 180°. Тогда
четырехугольник BC1B1K вписанный, а так как треугольник B1C1K
правильный, то РB = 180° – РC1B1K = 120°.
-
5.38.
-
Пусть BM — медиана, AK — биссектриса
треугольника ABC и BM^AK. Прямая AK является биссектрисой и
высотой треугольника ABM, поэтому AM = AB, т. е. AC = 2AM = 2AB.
Следовательно, AB = 2, BC = 3 и AC = 4.
-
5.39.
-
Пусть a и b — катеты, c — гипотенуза
данного треугольника. Если числа a и b нечетные, то a2 + b2 при
делении на 4 дает остаток 2 и не может быть квадратом целого числа.
Поэтому одно из чисел a и b четное, а другое нечетное; пусть для
определенности a = 2p. Числа b и c нечетные, поэтому c + b = 2q
и c – b = 2r. Следовательно 4p2 = a2 = c2 – b2 = 4qr. Если бы числа q
и r имели общий делитель d, то на d делились бы
числа
и c = q + r. Поэтому числа q и r
взаимно просты, а так как p2 = qr, то q = m2 и r = n2. В итоге
получаем a = 2mn, b = m2 – n2 и c = m2 + n2.
Легко проверить также, что если a = 2mn, b = m2 – n2 и c = m2 + n2,
то a2 + b2 = c2.
-
5.40.
-
Пусть p — полупериметр треугольника, а a,b,c —
длины его сторон. По формуле Герона S2 = p(p – a)(p – b)(p – c). С другой
стороны, S2 = p2r2 = p2, так как r = 1. Поэтому p = (p – a)(p – b)(p – c).
Если ввести неизвестные x = p – a, y = p – b, z = p – c, то это уравнение
перепишется в виде x + y + z = xyz. Заметим, что число p целое или
полуцелое (т. е. число вида (2n + 1)/2, где n целое), поэтому все
числа x,y,z одновременно целые или полуцелые. Но если они
полуцелые, то число x + y + z полуцелое, а число xyz имеет вид m/8,
где число m нечетное. Следовательно, числа x,y,z целые.
Пусть для определенности x Ј y Ј z. Тогда xyz = x + y + z Ј 3z,
т. е. xy Ј 3. Возможны три случая.
1. x = 1, y = 1. Тогда 2 + z = z, чего не может быть.
2. x = 1, y = 2. Тогда 3 + z = 2z, т. е. z = 3.
3. x = 1, y = 3. Тогда 4 + z = 3z, т. е. z = 2 < y, чего не может быть.
Итак, x = 1,y = 2, z = 3. Поэтому p = x + y + z = 6 и a = p – x = 5, b = 4, c = 3
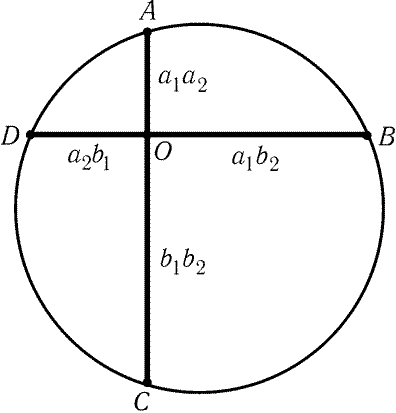
Рис. 5.3
5.41. Пусть a1 и b1, a2 и b2- катеты двух
различных пифагоровых треугольников, c1 и c2- их гипотенузы.
Возьмем две перпендикулярные прямые и отложим на них
отрезки OA = a1a2, OB = a1b2, OC = b1b2 и OD = a2b1 (рис. 5.3). Так
как OA · OC = OB · OD, то четырехугольник ABCD вписанный.
Согласно задаче 2.72 4R2 = OA2 + OB2 + OD2 = (c1c2)2,
т. е. R = c1c2/2. Увеличив, если нужно, четырехугольник ABCD в два
раза, получим искомый четырехугольник.
5.42. а) Длины гипотенуз прямоугольных треугольников с
катетами 5 и 12, 9 и 12 равны 13 и 15. Приложив равные катеты этих
треугольников друг к другу, получим треугольник площади 12(5 + 9)/2 = 84.
б) Предположим сначала, что длина наименьшей стороны данного
треугольника- четное число, т. е. длины сторон треугольника
равны 2n, 2n + 1, 2n + 2. Тогда по формуле Герона
16S2 = (6n + 3)(2n + 3)(2n + 1)(2n – 1) = 4(3n2 + 6n + 2)(4n2 – 1) + 4n2 – 1.
Получено противоречие, так как число, стоящее в правой части, не
делится на 4. Следовательно, длины сторон треугольника равны 2n – 1, 2n
и 2n + 1, причем S2 = 3n2(n2 – 1). Поэтому S = nk, где k — целое
число, и k2 = 3(n2 – 1). Ясно также, что k — длина высоты,
опущенной на сторону 2n. Эта высота делит исходный треугольник на
два прямоугольных треугольника с общим катетом k и гипотенузами 2n + 1
и 2n – 1; квадраты длин других катетов этих треугольников равны
(2n±1)2 – k2 = 4n2±4n + 1 – 3n2 + 3 = (n±2)2.
-
5.43.
-
а) Так как AB2 – AB12 = BB12 = BC2 – (AC±AB1)2,
то AB1 = ±(AB2 + AC2 – BC2)/2AC.
б) Пусть диагонали AC и BD пересекаются в точке O. Докажем,
например, что число q = BO/OD рациональное (тогда число OD = BD/(q + 1)
тоже рациональное). Проведем в треугольниках ABC и ADC
высоты BB1 и DD1. Согласно задаче а) числа AB1 и CD1
рациональные, а значит, число B1D1 тоже рациональное. Пусть E
- точка пересечения прямой BB1 и прямой, проходящей через
точку D параллельно AC. В прямоугольном треугольнике BDE
катет ED = B1D1 и гипотенуза BD — рациональные числа, поэтому
число BE2 тоже рациональное. Из треугольников ABB1 и CDD1
получаем, что числа BB12 и DD12 рациональные. А так как
BE2 = (BB1 + DD1)2 = BB12 + DD12 + 2BB1 · DD1, то
число BB1 · DD1 рациональное. Следовательно,
число BO/OD = BB1/DD1 = BB1 · DD1/DD12 рациональное.
-
5.44.
-
В треугольниках ABC и A1B1C1 не может быть двух
пар соответственных углов, составляющих в сумме 180°, так как
иначе их сумма равна 360° и третьи углы треугольников должны
быть нулевыми. Предположим теперь, что углы первого треугольника
равны a,b и g, а углы второго равны 180° – a,b
и g. Сумма углов двух треугольников равна 360°,
поэтому 180° + 2b + 2g
= 360°,
т. е. b + g
= 180°. Следовательно,
a
= 90° = 180° – a.
-
5.45.
-
Ясно, что
и
, поэтому
.
Аналогично
и
,
т. е. DABC = DA1B1C1. Кроме того, ABA1B1
и ACA1C1- параллелограммы. Значит, отрезки BB1 и CC1
проходят через середину отрезка AA1.
-
5.46.
-
Так как РMAO = РPAO, то AMOP — ромб.
Аналогично BNOQ — ромб. Следовательно, MN = MO + ON = AM + BN
и OP + PQ + QO = AP + PQ + QB = AB.
-
5.47.
-
а) Проведем через вершины треугольника ABC прямые,
параллельные его противоположным сторонам. В результате получим
треугольник A1B1C1, серединами сторон которого являются
точки A,B и C. Высоты треугольника ABC являются серединными
перпендикулярами к сторонам треугольника A1B1C1, поэтому центр
описанной окружности треугольника A1B1C1 является точкой
пересечения высот треугольника ABC.
б) Точка H является центром описанной окружности
треугольника A1B1C1, поэтому 4R2 = B1H2 = B1A2 + AH2 = BC2 + AH2.
Следовательно,
| AH2 = 4R2 – BC2 = |
ж
и
|
1
sin 2a
|
– 1 |
ц
ш
|
BC2 = (BCctg a)2
|
.
-
5.48.
-
Пусть AD — биссектриса равнобедренного
треугольника ABC с основанием AB и углом 36° при
вершине C. Тогда треугольник ACD равнобедренный и D
ABC ~ DBDA. Поэтому CD = AD = AB = 2xBC и DB = 2xAB = 4x2BC, а
значит, BC = CD + DB = (2x + 4x2)BC.
-
5.49.
-
Пусть B1 и B2- проекции точки A на
биссектрисы внутреннего и внешнего углов при вершине B, M —
середина стороны AB. Так как биссектрисы внутреннего и внешнего углов
перпендикулярны, то AB1BB2- прямоугольник, и его
диагональ B1B2 проходит через точку M. Кроме того,
РB1MB = 180° – 2РMBB1 = 180° – РB.
Следовательно, B1B2||BC, а значит, прямая B1B2 совпадает с
прямой l, соединяющей середины сторон AB и AC. Аналогично
доказывается, что проекции точки A на биссектрисы углов при
вершине C лежат на прямой l.
-
5.50.
-
Предположим, что биссектрисы углов A и B равны,
но a > b. Тогда
и
, т. е.
.
Перемножая полученные неравенства, приходим к противоречию, так
как la = 2bccos (A/2)/(b + c) и lb = 2accos (B/2)/(a + c) (см.
задачу 4.47).
-
5.51.
-
а) Согласно задаче 4.47 длина биссектрисы угла B
треугольника ABC равна 2accos (B/2)/(a + c), поэтому достаточно
проверить, что система уравнений ac/(a + c) = p, a2 + c2 – 2accos B = q имеет
(с точностью до перестановки чисел a и c) единственное положительное
решение. Пусть a + c = u. Тогда ac = pu и q = u2 – 2pu(1 + cos b).
Произведение корней этого квадратного уравнения относительно u
равно – q, поэтому оно имеет единственный положительный корень. Ясно,
что система уравнений a + c = u, ac = pu имеет единственное решение.
б) В треугольниках AA1B и CC1B равны стороны AA1 и CC1,
углы при вершине B и биссектрисы углов при вершине B.
Следовательно, эти треугольники равны, а значит, AB = BC или AB = BC1.
Второе равенство выполняться не может.
-
5.52.
-
Пусть точки M и N лежат на сторонах AB и AC.
Если r1- радиус окружности с центром на отрезке MN, касающейся
сторон AB и AC, то SAMN = qr1, где q = (AM + AN)/2. Прямая MN
проходит через центр вписанной окружности тогда и только тогда,
когда r1 = r, т. е. SAMN/q = SABC/p = SBCNM/(p – q).
-
5.53.
-
а) Возьмем на продолжении отрезка AC за точку C
такую точку Bў, что CBў = CB. Треугольник BCBў равнобедренный,
поэтому РAEB = РACB = 2РCBBў, а значит, E — центр
описанной окружности треугольника ABBў. Следовательно, точка F
делит отрезок ABў пополам; поэтому прямая C1F делит пополам
периметр треугольника ABC.
б) Легко проверить, что прямая, проведенная через точку C
параллельно BBў, является биссектрисой угла ACB. А так как C1F||
BBў, то прямая C1F — биссектриса угла треугольника с вершинами в
серединах сторон треугольника ABC. Биссектрисы этого треугольника
пересекаются в одной точке.
-
5.54.
-
Пусть X — точка пересечения прямых AD2 и CD1;
M,E1 и E2- проекции точек X,D1 и D2 на прямую AC.
Тогда CE2 = CD2sin g
= asin g и AE1 = csin a. Так
как asin g
= csin a, то CE2 = AE1 = q. Поэтому
|
|
XM
AM
|
= |
D2E2
AE2
|
= |
acos g
b + q
|
и
|
XM
CM
|
= |
ccos a
b + q
|
. |
|
Следовательно, AM : CM = ccos a : acos g. Высота BH
делит сторону AC в таком же отношении.
-
5.55.
-
а) По теореме косинусов
B1C12 = AC12 + AB12 – 2AC1 · AB1 · cos (90° + a),
т. е.
| a12 = |
c2
2
|
+ |
b2
2
|
+ bcsin a
= |
b2 + c2
2
|
+ 2S
|
. Записывая аналогичные равенства для b12
и c12 и складывая их, получаем требуемое.
б) Для остроугольного треугольника ABC, прибавив к S площади
треугольников ABC1,AB1C и A1BC и прибавив к S1 площади
треугольников AB1C1,A1BC1 и A1B1C, получим одинаковые
величины (для треугольника с тупым углом A площадь
треугольника AB1C1 следует взять со знаком минус). Поэтому
S1 = S + (a2 + b2 + c2)/4 – (abcos g + accos b + bccos a)/4.
Остается заметить, что
abcos g + bccos a + accos b
= 2S(ctg g + ctg a + ctg b) = (a2 + b2 + c2)/2 (см. задачу 12.44, а)).
-
5.56.
-
Докажем сначала, что точка Bў лежит на описанной
окружности треугольника AHC, где H — точка пересечения высот
треугольника ABC.
Р(ABў,BўC) = Р(AA1,CC1) = Р(AA1,BC) + Р(BC,AB) + Р(AB,CC1) = Р(BC,AB).
Но, как следует из решения задачи 5.10,
Р(BC,AB) = Р(AH,HC),
поэтому точки A,Bў,H и C лежат на
одной окружности, причем эта окружность симметрична описанной
окружности треугольника ABC относительно прямой AC. Следовательно,
обе эти окружности имеют радиус R, а значит,
BўH = 2Rsin BўAH = 2Rcos a.
Аналогично AўH = 2Rcos a = CўH. Решение задачи а) тем самым
завершено, а для решения задачи б) остается заметить, что D
AўBўCў ~ DABC, так как после поворота треугольника AўBўCў
на угол a его стороны будут параллельны сторонам треугольника ABC.
-
5.57.
-
Пусть из вершины A окружности, вписанные в углы B и C, видны под углами
ab и ac, а радиусы этих окружностей равны rb и rc. Тогда
|
b = rc |
ж
и
|
ctg |
g
2
|
+ ctg |
ac
2
|
ц
ш
|
и c = rb |
ж
и
|
ctg |
b
2
|
+ ctg |
ab
2
|
ц
ш
|
. |
|
Поэтому равенство ab = ac эквивалентно равенству
|
|
b
rc
|
– ctg |
g
2
|
= |
c
rb
|
– ctg |
b
2
|
, т. е. |
b
rc
|
– |
a + b – c
2r
|
= |
c
rb
|
– |
a – b + c
2r
|
. |
|
После несложных преобразований получаем равенство
Ясно, что из этого равенства и из равенства
следует равенство
.
-
5.58.
-
Пусть a1 = BA1, a2 = A1C, b1 = CB1, b2 = B1A, c1 = AC1
и c2 = C1B. Произведения длин отрезков секущих, проходящих через
одну точку, равны, поэтому a1(a1 + x) = c2(c2 – z),
т. е. a1x + c2z = c22 – a12. Аналогично получаем для x,y и z еще
два уравнения: b1y + a2x = a22 – b12 и c1z + b2y = b22 – c12.
Домножим первое уравнение на b2n, а второе и третье на c2n
и a2n и сложим полученные уравнения. Так как, например,
c2bn – c1an = 0 по условию, то в правой части получим нуль. В левой
части, например, коэффициент при x равен
a1b2n + a2c2n = (acnb2n + abnc2n)/(bn + cn) = abncn.
Поэтому abncnx + bancny + canbnz = 0. Поделив обе части равенства
на (abc)n, получим требуемое.
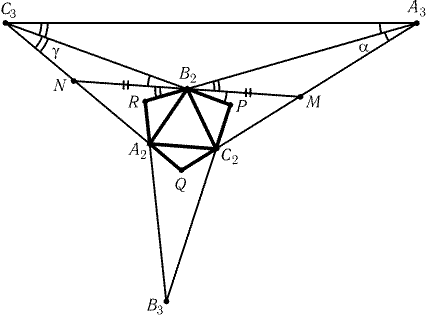
Рис. 5.4
5.59. Пусть в исходном треугольнике РA = 3a, РB = 3b и РC = 3g. Возьмем равносторонний
треугольник A2B2C2 и построим на его сторонах как на основаниях
равнобедренные треугольники A2B2R, B2C2P и C2A2Q с углами при
основаниях 60° – g, 60° – a, 60° – b
соответственно (рис. 5.4). Продолжим боковые стороны этих треугольников
за точки A2,B2 и C2 и обозначим точку пересечения продолжений
сторон RB2 и QC2 через A3, PC2 и RA2 через B3,
QA2 и PB2 через C3. Проведем через B2 прямую,
параллельную A2C2, и обозначим через M и N точки ее пересечения
с прямыми QA3 и QC3. Ясно, что B2- середина отрезка NM.
Вычислим углы треугольников B2C3N и B2A3M:
РC3B2N = РPB2M = РC2B2M – РC2B2P = a;
РB2NC3 = 180° – РC2A2Q = 120° + b,
значит, РB2C3N = 180° – a – (120° + b) = g.
Аналогично РA3B2M = g и РB2A3M = a.
Следовательно, DB2C3N ~ DA3B2M. Значит,
C3B2 : B2A3 = C3N : B2M, а так как B2M = B2N
и РC3B2A3 = РC3NB2, то C3B2 :
B2A3 = C3N : NB2 и DC3B2A3 ~ DC3NB2,
следовательно, РB2C3A3 = g. Аналогично РA2C3B3 = g, а значит, РA3C3B3 = 3g
= РC и C3B2,C3A2- триссектрисы угла C3 треугольника A3B3C3.
Аналогичные рассуждения для вершин A3 и B3 показывают,
что DABC ~ DA3B3C3, а точки пересечения
триссектрис треугольника A3B3C3 образуют правильный
треугольник A2B2C2.
-
5.60.
-
Точка A1 лежит на биссектрисе угла BAC, поэтому
точка A лежит на продолжении биссектрисы угла B2A1C2. Кроме
того,
РB2AC2 = a = (180° – РB2A1C2) / 2. Поэтому A
- центр вневписанной окружности треугольника B2A1C2 (см.
задачу 5.3). Пусть D — точка пересечения прямых AB и CB2.
Тогда РAB2C2 = РAB2D = 180° – РB2AD – РADB2 = 180° – g – (60° + a) = 60° + b. А так как
РAB2C = 180° – (a + b) – (b + g) = 120° – b,
то РCB2C2 = РAB2C – РAB2C2 = 60° – 2b.
Аналогично РAB2A2 = 60° – 2b. Поэтому
РA2B2C2 = РAB2C – РAB2A2 – РCB2C2 = 3b.
Аналогично РB2A2C2 = 3a и РA2C2B2 = 3g.
-
5.61.
-
Длина общей касательной к данным окружностям равна
, поэтому
|
uactg |
a
2
|
+ 2 |
Ц
|
uaub
|
+ ubctg |
b
2
|
= c, |
|
т. е.
| a12 + 2a1b1 |
ж
Ц
|
|
+ b12 = c12
|
.
Согласно задаче 12.36, б)
|
tg |
a
2
|
tg |
b
2
|
= |
r
p
|
ctg |
g
2
|
= |
r
p
|
· |
p – c
r
|
< 1. |
|
Поэтому существует угол g1, для которого
Мы проверили, что треугольник со сторонами a1, b1, c1
действительно существует; кроме того, угол между сторонами a1
и b1 равен g1. Поэтому диаметр описанной окружности
рассматриваемого треугольника равен
поскольку
.
-
5.62.
-
Пусть u1 и u2 - радиусы окружностей S1 и S2. Согласно
задаче 5.61 радиус описанной окружности треугольника со сторонами
,
,
равен Цp/2; кроме того, в этом треугольнике угол между сторонами
и
тупой. Пусть j1, j2 и gў -
острые углы, опирающиеся на хорды
,
и
.
Тогда j1 + j2 = gў; при этом u1 и u2 однозначно
восстанавливаются по j1 и j2. Аналогично получаем равенства
|
j1 + j2 = gў = j4 + j5, (1) |
|
|
j2 + j3 = aў = j5 + j6, (2) |
|
|
j3 + j4 = bў = j6 + j7. (3) |
|
Сложим равенства (1) и (3) и вычтем из них равенство (2). В результате получим
j1 = j7. Из этого следует, что радиусы окружностей S1 и S7
равны.
-
5.63.
-
Пусть ri - радиус окружности Si, hi - высота треугольника ABC,
опущенная из вершины A при i = 3k + 1, из вершины B при i = 3k + 2, из вершины
C при i = 3k. Формулу из задачи 5.9 а) можно записать в виде
|
|
ж
и
|
r
ri
|
– 1 |
ц
ш
|
|
ж
и
|
r
ri + 1
|
– 1 |
ц
ш
|
= 1 – |
2r
hi + 2
|
. |
| (i) |
Перемножим равенства (i) и (i + 2), а затем поделим их произведение
на (i + 1). В результате получим
|
|
ж
и
|
r
ri
|
– 1 |
ц
ш
|
|
ж
и
|
r
ri + 3
|
– 1 |
ц
ш
|
= |
ж
и
|
1 – |
2r
hi + 1
|
ц
ш
|
|
ж
и
|
1 – |
2r
hi + 2
|
ц
ш
| / |
|
ж
и
|
1 – |
2r
hi
|
ц
ш
|
. |
|
Правая часть полученного выражения не изменяется при замене i на i + 3.
Поэтому
|
|
ж
и
|
r
ri
|
– 1 |
ц
ш
|
|
ж
и
|
r
ri + 3
|
– 1 |
ц
ш
|
= |
ж
и
|
r
ri + 3
|
– 1 |
ц
ш
|
|
ж
и
|
r
ri + 6
|
– 1 |
ц
ш
|
. |
|
Предполагается, что все треугольники невырожденные. В таком случае можно
сократить обе части на
, поэтому ri = ri + 6.
-
5.64.
-
Пусть при проекции на прямую, перпендикулярную
прямой A1B1, точки A,B и C переходят в Aў,Bў и Cў,
точка C1- в Q, а две точки A1 и B1- в одну
точку P. Так как
|
A1B
|
: |
A1C
|
= |
PBў
|
: |
PCў
|
, |
B1C
|
: |
B1A
|
= |
PCў
|
: |
PAў
|
|
и
, то
|
|
· |
|
· |
|
= |
|
· |
|
· |
|
= |
|
· |
|
= |
bў
aў
|
· |
aў + x
bў + x
|
|
,
где |x| = PQ. Равенство
|
bў
aў
|
· |
aў + x
bў + x
|
= 1
|
эквивалентно тому, что x = 0 (нужно учесть, что aў № bў, так
как Aў № Bў). А равенство x = 0 означает, что P = Q, т. е.
точка C1 лежит на прямой A1B1.
-
5.65.
-
Пусть точка P лежит на дуге BC описанной окружности
треугольника ABC. Тогда
|
|
= – |
BPcos PBC
CPcos PCB
|
, |
|
= – |
CPcos PCA
APcos PAC
|
|
и
.
Перемножая эти равенства и учитывая, что РPAC = РPBC, РPAB = РPCB и РPCA + РPBA = 180°, получаем
.
-
5.66.
-
Пусть O,O1 и O2- центры окружностей S,S1
и S2; X — точка пересечения прямых O1O2 и A1A2.
Применяя теорему Менелая к треугольнику OO1O2 и точкам A1,A2
и X, получаем
|
O1X
O2X
|
· |
O2A2
OA2
|
· |
OA1
O1A1
|
= 1
|
,
а значит, O1X : O2X = R1 : R2, где R1 и R2-
радиусы окружностей S1 и S2. Следовательно, X — точка
пересечения общих внешних или общих внутренних касательных к
окружностям S1 и S2.
-
5.67.
-
а) Пусть для определенности РB < РC.
Тогда РDAE = РADE = РB + РA/2, а значит, РCAE = РB. Так как
|
|
BE
AB
|
= |
sin BAE
sin AEB
|
и
|
AC
CE
|
= |
sin AEC
sin CAE
|
, |
|
то
|
|
BE
CE
|
= |
csin BAE
bsin CAE
|
= |
csin (A + B)
bsin B
|
= |
csin C
bsin B
|
= |
c2
b2
|
. |
|
б) В задаче а) точка E лежит на продолжении стороны BC,
так как РADC = РBAD + РB > РCAD. Поэтому, используя
результат задачи а) и теорему Менелая, получаем требуемое.
-
5.68.
-
Так как РBCE = 90° – РB/2, то РBCE = РBEC, а значит, BE = BC. Поэтому CF : KF = BE :
BK = BC : BK и AE : KE = CA : CK = BC : BK. Пусть
прямая EF пересекает AC в точке D. По теореме Менелая
|
AD
CD
|
· |
CF
KF
|
· |
KE
AE
|
= 1
|
. Учитывая,
что CF : KF = AE : KE, получаем требуемое.
-
5.69.
-
Доказательство аналогично решению задачи 5.87; нужно
только рассмотреть отношение ориентированных отрезков и углов.
-
5.70.
-
Пусть A2,B2,C2- точки пересечения прямых BC
и B1C1, AC и A1C1, AB и A1B1. Применим теорему
Менелая к следующим треугольникам и точкам на их сторонах: OAB
и (A1,B1,C2), OBC и (B1,C1,A2), OAC и (A1,C1,B2).
Тогда
|
|
|
· |
|
· |
|
= 1, |
|
· |
|
· |
|
= 1, |
|
· |
|
· |
|
= 1. |
|
Перемножая эти равенства, получаем
Из теоремы Менелая следует, что точки A2,B2,C2 лежат на одной
прямой.
-
5.71.
-
Рассмотрим треугольник A0B0C0, образованный
прямыми A1B2, B1C2 и C1A2 (A0- точка пересечения
прямых A1B2 и A2C1 и т. д.), и применим для него теорему
Менелая к следующим пяти тройкам точек: (A,B2,C1), (B,C2,A1),
(C,A2,B1), (A1,B1,C1) и (A2,B2,C2).
В результате получим
Перемножая эти равенства, получаем
, а значит,
точки A,B и C лежат на одной прямой.
-
5.72.
-
Пусть N — точка пересечения прямых AD и KQ,
Pў- точка пересечения прямых KL и MN. Применяя теорему
Дезарга к треугольникам KBL и NDM, получаем, что точки Pў,A и C
лежат на одной прямой. Значит, Pў = P.
-
5.73.
-
Достаточно применить теорему Дезарга к
треугольникам AED и BFC и теорему Паппа к тройкам точек (B,E,C)
и (A,F,D).
-
5.74.
-
а) Пусть R — точка пересечения прямых KL и MN.
Применяя теорему Паппа к тройкам точек (P,L,N) и (Q,M,K),
получаем, что точки A,C и R лежат на одной прямой.
б) Применяя теорему Дезарга к треугольникам NDM и LBK,
получаем, что точки пересечения прямых ND и LB, DM и BK,
NM и LK лежат на одной прямой.
-
5.75.
-
Воспользуемся результатом задачи 5.74, а). В качестве
точек P и Q возьмем точки P2 и P4, в качестве A и C —
точки C1 и P1, в качестве K,L,M и N — точки P5,A1,B1
и P3. В итоге получим, что прямая P6C1 проходит через
точку P1.
-
5.76.
-
Согласно теореме Дезарга точки пересечения прямых AC и DF,
CE и FB, EA и BD лежат на одной прямой. Это означает,
что точки пересечения прямых AўBў и DўEў, CўDў и FўAў,
EўFў и BўCў лежат на одной прямой.
-
5.77.
-
а) Эта задача является переформулировкой задачи 5.64,
так как число
имеет знак минус, если
точка A1 лежит на отрезке BC, и знак плюс, если она лежит вне
отрезка BC.
б) Предположим сначала, что прямые AA1,BB1 и CC1 пересекаются
в точке M. Любые три вектора плоскости линейно зависимы,
т. е. существуют такие числа l,m и n (не все равные нулю),
что
| l |
®
AM
|
+ m |
®
BM
|
+ n |
®
CM
|
= 0
|
. Рассмотрим проекцию на
прямую BC параллельно прямой AM. При этой проекции точки A и M
переходят в A1, а точки B и C переходят сами в себя.
Поэтому
,
т. е.
.
Аналогично
и
. Перемножая эти
равенства, получаем требуемое. В случае, когда прямые AA1,BB1
и CC1 параллельны, для доказательства достаточно заметить,
что
и
.
Предположим теперь, что выполняется указанное соотношение,
и докажем, что тогда прямые AA1,BB1 и CC1 пересекаются в одной
точке. Пусть C1*- точка пересечения прямой AB с прямой,
проходящей через точку C и точку пересечения прямых AA1 и BB1.
Для точки C1* выполняется такое же соотношение, как и для
точки C1.
Поэтому
.
Следовательно, C1* = C1, т. е. прямые AA1,BB1 и CC1
пересекаются в одной точке.
Можно проверить также, что если выполняется указанное соотношение
и две из прямых AA1,BB1 и CC1 параллельны, то третья
прямая им параллельна.
-
5.78.
-
Ясно, что AB1 = AC1, BA1 = BC1 и CA1 = CB1, причем
в случае вписанной окружности на сторонах треугольника ABC
лежат три точки, а в случае вневписанной- одна точка. Остается
воспользоваться теоремой Чевы.
-
5.79.
-
Пусть вневписанные окружности касаются сторон BC, CA и AB в точках A1, B1 и C1. Тогда
|
|
BA1
CA1
|
|
C B1
A B1
|
|
AC1
BC1
|
= |
p – c
p – b
|
|
p – a
p – c
|
|
p – b
p – a
|
= 1. |
|
-
5.80.
-
Пусть AA1,BB1 и CC1- высоты
треугольника ABC. Тогда
|
|
AC1
C1B
|
· |
BA1
A1C
|
· |
CB1
B1A
|
= |
bcos A
acos B
|
· |
ccos B
bcos C
|
· |
acos C
ccos A
|
= 1. |
|
-
5.81.
-
Пусть A2,B2 и C2- середины сторон BC,CA
и AB. Рассматриваемые прямые проходят через вершины
треугольника A2B2C2, причем в задаче а) они делят его стороны в
таких же отношениях, в каких прямые AP,BP и CP делят стороны
треугольника ABC, а в задаче б) они делят их в обратных отношениях.
Остается воспользоваться теоремой Чевы.
-
5.82.
-
Так как DAC1B2 ~ DBC1A1
и DAB1C2 ~ DCB1A1,
то AB2 · C1B = AC1 · BA1 и AC2 · CB1 = A1C · B1A.
Поэтому
|
|
AB2
AC2
|
= |
AC1
C1B
|
· |
BA1
A1C
|
· |
CB1
B1A
|
= 1. |
|
-
5.83.
-
Пусть прямые AA1,BB1 и CC1 пересекают
прямые BC,CA и AB в точках A2,B2 и C2.
а) Если РB + b
= 180° и РC + g
= 180°, то
|
BA2
A2C
|
= |
SABA1
SACA1
|
= |
AB · BA1sin (B + b)
AC · CA1sin (C + g)
|
= |
AB
AC
|
· |
sin g
sin b
|
· |
sin (B + b)
sin (C + g)
|
|
.
Последнее выражение равно
во всех случаях.
Запишем аналогичные выражения для
и
и перемножим их. Остается
воспользоваться теоремой Чевы.
б) Точка A2 лежит вне отрезка BC, только если ровно один
из углов b и g больше соответствующего ему угла B или C.
Поэтому
|
|
|
= |
AB
AC
|
· |
sin g
sin b
|
· |
sin (B – b)
sin (C – g)
|
. |
|
-
5.84.
-
Легко проверить, что эта задача является частным случаем
задачи 5.83.
Замечание.
Аналогичное утверждение верно и для вневписанной окружности.
-
5.85.
-
Решение задачи очевидным образом следует из теоремы
Чевы.
-
5.86.
-
Применяя теорему синусов к треугольникам ACC1
и BCC1, получаем
и
,
т. е.
|
AC1
C1B
|
= |
sin ACC1
sin C1CB
|
· |
sin B
sin A
|
|
. Аналогично
|
BA1
A1C
|
= |
sin BAA1
sin A1AC
|
· |
sin C
sin B
|
|
и
|
CB1
B1A
|
= |
sin CBB1
sin B1BA
|
· |
sin A
sin C
|
|
.
Для завершения доказательства остается перемножить эти равенства.
Замечание.
Аналогичное утверждение справедливо и для отношений ориентированных
отрезков и углов в том случае, когда точки взяты на продолжениях сторон.
-
5.87.
-
Можно считать, что точки A2,B2 и C2 лежат на
сторонах треугольника ABC. Согласно задаче 5.86
|
|
AC2
C2B
|
· |
BA2
A2C
|
· |
CB2
B2A
|
= |
sin ACC2
sin C2CB
|
· |
sin BAA2
sin A2AC
|
· |
sin CBB2
sin B2BA
|
. |
|
Так как прямые AA2,BB2 и CC2 симметричны прямым AA1,BB1
и CC1 относительно биссектрис, то РACC2 = РC1CB,РC2CB = РACC1 и т. д., поэтому
|
|
sin ACC2
sin C2CB
|
· |
sin BAA2
sin A2AC
|
· |
sin CBB2
sin B2BA
|
= |
sin C1CB
sin ACC1
|
· |
sin A1AC
sin BAA1
|
· |
sin B1BA
sin CBB1
|
= |
|
|
= |
C1B
AC1
|
· |
A1C
BA1
|
· |
B1A
CB1
|
= 1. |
|
Следовательно,
|
AC2
C2B
|
· |
BA2
A2C
|
· |
CB2
B2A
|
= 1
|
,
т. е. прямые AA2, BB2 и CC2 пересекаются в одной точке.
Замечание.
Утверждение остается верным и в том случае, когда точки A1,B1
и C1 взяты на продолжениях сторон, если только точка P не лежит на
описанной окружности S треугольника ABC; если же P лежит на
окружности S, то прямые AA2,BB2 и CC2 параллельны (см.
задачу 2.92).
-
5.88.
-
Пусть диагонали AD и BE данного
шестиугольника ABCDEF пересекаются в точке P; K и L —
середины сторон AB и ED. Так как ABDE — трапеция, отрезок KL
проходит через точку P (задача 19.2). По теореме синусов sin APK : sin AKP = AK : AP
и sin BPK : sin BKP = BK : BP. Так как sin AKP = sin BKP
и AK = BK, то sin APK : sin BPK = BP : AP = BE : AD.
Аналогичные соотношения можно записать и для отрезков, соединяющих
середины двух других пар противоположных сторон. Перемножая эти
соотношения и применяя результат задачи 5.86 к треугольнику,
образованному прямыми AD,BE и CF, получаем требуемое.
-
5.89.
-
Рассмотрим гомотетию с центром P и коэффициентом 2.
Так как PA1A3A2- прямоугольник, то при этой гомотетии
прямая A1A2 переходит в прямую la, проходящую через точку A3,
причем прямые la и A3P симметричны относительно прямой A3A.
Прямая A3A делит пополам угол B3A3C3 (задача 1.57, а)).
Аналогично доказывается, что прямые lb и lc симметричны
прямым B3P и C3P относительно биссектрис
треугольника A3B3C3. Следовательно, прямые la,lb и lc
пересекаются в одной точке или параллельны (задача 5.87), а значит, в
одной точке пересекаются и прямые A1A2,B1B2,C1C2.
-
5.90.
-
Согласно задачам 5.86 и 5.77, б)
|
|
sin ASP
sin PSD
|
· |
sin DAP
sin PAS
|
· |
sin SDP
sin PDA
|
= 1 = |
sin ASQ
sin QSD
|
· |
sin DAQ
sin QAS
|
· |
sin SDQ
sin QDA
|
. |
|
Но РDAP = РSDQ,
РSDP = РDAQ,
РPAS = РQDA
и РPDA = РQAS.
Поэтому sin ASP : sin PSD = sin ASQ : sin QSD. Из этого следует, что точки S,P и Q лежат на одной
прямой, так как функция
монотонна по x:
|
|
d
d x
|
|
ж
и
|
sin (a – x)
sin x
|
ц
ш
|
= – |
sin a
sin 2x
|
. |
|
-
5.91.
-
Второе равенство из задачи 2.59, а) означает, что
|
|
ж
и
|
sin A2A1C1
sin A2A1B1
|
ц
ш
|
2
|
= |
sin A2AC1
sin A2AB1
|
. |
|
Поэтому
|
|
ж
и
|
sin A2A1C1
sin A2A1B1
|
· |
sin B2B1A1
sin B2B1C1
|
· |
sin C2C1B1
sin C2C1A1
|
ц
ш
|
2
|
= 1. |
|
-
5.92.
-
Согласно задаче 3.42, а) отрезок A1A2 является биссектрисой треугольника
A1BC. Поэтому
|
|
BA2
CA2
|
= |
BA1
CA1
|
= |
sin BAA1
sin CCA1
|
. |
|
Из того, что прямые AA1, BB1 и CC1 пересекаются в одной точке,
следует, что
|
|
sin BAA1
sin CCA1
|
· |
sin CBB1
sin ABB1
|
· |
sin ACC1
sin BCC1
|
= 1. |
|
Поэтому
|
|
BA2
CA2
|
· |
CB2
AB2
|
· |
AC2
BC2
|
= 1, |
|
а значит, прямые AA2, BB2 и CC2 пересекаются в одной точке.
-
5.93.
-
а) По теореме
Чевы
|
AC1
C1B
|
= |
CA1
A1B
|
· |
AB1
B1C
|
|
, а по
теореме синусов
|
CA1 = |
CAsin CAA1
sin AA1B
|
, A1B = |
ABsin BAA1
AA1B
|
, |
|
|
AB1 = |
ABsin ABB1
sin AB1B
|
, B1C = |
BCsin CBB1
sin AB1B
|
. |
|
Подставляя эти четыре равенства в предыдущее равенство и учитывая,
что AC = BC, получаем требуемое.
б) Обозначим точки пересечения прямых CM и CN с основанием AB
через M1 и N1. Нужно доказать, что M1 = N1. Из а) следует,
что AM1 : M1B = AN1 : N1B, т. е. M1 = N1.
-
5.94.
-
Пусть отрезки BM и BN пересекают сторону AC в
точках P и Q. Тогда
|
|
sin PBB1
sin PBA
|
= |
sin PBB1
sin BPB1
|
· |
sin APB
sin PBA
|
= |
PB1
BB1
|
· |
AB
PA
|
. |
|
Если O — точка пересечения биссектрис треугольника ABC, то
|
AP
PB1
|
· |
B1O
OB
|
· |
BC1
C1A
|
= 1
|
,
а значит,
|
sin PBB1
sin PBA
|
= |
AB
BB1
|
· |
B1O
OB
|
· |
BC1
C1A
|
|
.
Заметив, что BC1 : C1A = BC : CA, и проведя аналогичные
вычисления для sin QBB1 : sin QBC, получим
sin PBB1 : sin PBA = sin QBB1 : sin QBC.
А так как РABB1 = РCBB1, то РPBB1 = РQBB1.
-
5.95.
-
а) Пусть точка P лежит на дуге AC описанной
окружности треугольника ABC; A1,B1 и C1- основания
перпендикуляров, опущенных из точки P на прямые BC,CA и AB. Сумма
углов при вершинах A1 и C1 четырехугольника A1BC1P
равна 180°, поэтому РA1PC1 = 180° – РB = РAPC. Следовательно, РAPC1 = РA1PC, причем
одна из точек A1 и C1 (например, A1) лежит на стороне
треугольника, а другая- на продолжении стороны.
Четырехугольники AB1PC1 и A1B1PC вписанные, поэтому РAB1C1 = РAPC1 = РA1PC = РA1B1C, а значит, точка B1
лежит на отрезке A1C1.
б) Как и в задаче а), получаем
Р(AP,PC1) = Р(AB1,B1C) = Р(CB1,B1A1) = Р(CP,PA1).
Прибавляя Р(PC1,PC), получаем
Р(AP,PC) = Р(PC1,PA1) = Р(BC1,BA1) = Р(AB,PC),
т. е. точка P лежит на описанной окружности треугольника ABC.
-
5.96.
-
Пусть A1,B1 и C1- середины отрезков PA,PB
и PC; Oa,Ob и Oc- центры описанных окружностей
треугольников BCP,ACP и ABP. Точки A1,B1 и C1 являются
основаниями перпендикуляров, опущенных из точки P на стороны
треугольника OaObOc (или их продолжения). Точки A1,B1 и C1
лежат на одной прямой, поэтому точка P лежит на описанной окружности
треугольника OaObOc (см. задачу 5.95, б)).
-
5.97.
-
Пусть продолжение биссектрисы AD пересекает описанную
окружность треугольника ABC в точке P. Опустим из точки P
перпендикуляры PA1,PB1 и PC1 на прямые BC,CA и AB;
ясно, что A1- середина отрезка BC. При гомотетии с центром A,
переводящей P в D, точки B1 и C1 переходят в Bў и Cў, а
значит, точка A1 переходит в M, так как она лежит на
прямой B1C1 и PA1||DM.
-
5.98.
-
а) Решение задачи 5.95 проходит без изменений и в этом
случае.
б) Пусть A1 и B1- основания перпендикуляров, опущенных из
точки P на прямые BC и CA, а точки A2 и B2 прямых BC
и AC таковы, что Р(PA2,BC) = a
= Р(PB2,AC). Тогда
DPA1A2 ~ DPB1B2, поэтому точки A1 и B1
переходят в A2 и B2 при поворотной гомотетии с центром P,
причем РA1PA2 = 90° – a- угол поворота.
-
5.99.
-
а) Пусть угол между прямыми PC и AC равен j.
Тогда PA = 2Rsin j. Так как точки A1 и B1 лежат на окружности
с диаметром PC, угол между прямыми PA1 и A1B1 тоже
равен j. Поэтому PA1 = d/sin j, а значит, PA · PA1 = 2Rd.
б) Так как PA1^BC, то cos a
= sin j
= d/PA1. Остается
заметить, что PA1 = 2Rd/PA.
-
5.100.
-
Точки A1 и B1 лежат на окружности с диаметром PC,
поэтому A1B1 = PCsin A1CB1 = PCsin C. Пусть угол между прямыми AB
и A1B1 равен g и C1- проекция точки P на
прямую A1B1. Прямые A1B1 и B1C1 совпадают,
поэтому cos g
= PC/2R (см. задачу 5.99). Следовательно, длина
проекции отрезка AB на прямую A1B1 равна ABcos g
= (2Rsin C)PC/2R = PCsin C.
-
5.101.
-
. Пусть A1 и B1- основания перпендикуляров,
опущенных из точки P на прямые BC и AC. Точки A1 и B1 лежат
на окружности с диаметром PC. Так как sin A1CB1 = sin ACB,
хорды A1B1 этой окружности имеют фиксированную длину.
Следовательно, прямые A1B1 касаются фиксированной окружности.
-
5.102.
-
Пусть A1 и B1- основания перпендикуляров,
опущенных из точки P на прямые BC и CA. Тогда
Р(A1B1,PB1) = Р(A1C,PC) = ИBP/2.
Ясно также, что для всех точек P прямые PB1 имеют одно и
то же направление.
-
5.103.
-
Пусть P1 и P2 — диаметрально противоположные
точки описанной окружности треугольника ABC; Ai и Bi-
основания перпендикуляров, опущенных из точки Pi на прямые BC
и AC; M и N — середины сторон AC и BC; X — точка
пересечения прямых A1B1 и A2B2.
Согласно задаче 5.102
A1B1^A2B2. Остается проверить, что
Р(MX,XN) = Р(BC,AC). Так как AB2 = B1C, то XM —
медиана прямоугольного треугольника B1XB2.
Поэтому Р(XM,XB2) = Р(XB2,B2M).
Аналогично Р(XA1,XN) = Р(A1N,XA1).
Следовательно,
Р(MX,XN) = Р(XM,XB2) + Р(XB2,XA1) + Р(XA1,XN) = Р(XB2,B2M) + Р(A1N,XA1) + 90°.
А так как
Р(XB2,B2M) + Р(AC,CB) + Р(NA1,A1X) + 90° = 0°,
то Р(MN,XN) + Р(AC,CB) = 0°.
-
5.104.
-
Если точка R данной окружности такова, что
| Р( |
®
OP
|
, |
®
OR
|
) = (b + g)/2
|
, то OR^BC.
Остается проверить, что Р(OR,OQ) = Р(PA1,A1B1).
Но Р(OR,OQ) = a/2,
a
| Р(PA1,A1B1) = Р(PB,BC1) = Р( |
®
OP
|
, |
®
OA
|
)/2 = a/2
|
.
-
5.105.
-
Не теряя общности, можно считать, что описанные окружности
треугольников ABC и A1B1C1 совпадают. Определим углы
a, b и g, как в условии задачи 5.104.
Покажем, что точки с угловыми координатами
(a + b + g)/2, ( – a + b + g)/2,
(a – b + g)/2 и (a + b – g)/2 можно
взять в качестве точек P1, A1, B1 и C1.
Действительно, биссектриса угла A1OB1 задаётся угловой
координатой g/2, т.е. она параллельна PC; биссектриса
угла P1OA1 задаётся угловой координатой (b + g)/2,
т. е. она параллельна BC.
-
5.106.
-
Пусть прямые AC и PQ пересекаются в точке M.
Проведем в треугольнике MPC высоты PB1 и CA1. Тогда A1B1
- прямая Симсона точки P относительно треугольника ABC. Кроме
того, согласно задаче 1.53 Р(MB1,B1A1) = Р(CP,PM).
Ясно также, что Р(CP,PM) = Р(CA,AQ) = Р(MB1,AQ).
Следовательно, A1B1||AQ.
-
5.107.
-
Проведем хорду PQ, перпендикулярную BC. Пусть
точки Hў и Pў симметричны точкам H и P относительно
прямой BC; точка Hў лежит на описанной окружности треугольника ABC
(задача 5.10). Докажем сначала, что AQ||PўH. В самом деле,
Р(AHў,AQ) = Р(PHў,PQ) = Р(AHў,PўH). Прямая Симсона
точки P параллельна AQ (задача 5.106), т. е. она проходит через
середину стороны PPў треугольника PPўH и параллельна стороне PўH,
а значит, она проходит через середину стороны PH.
-
5.108.
-
Пусть Ha,Hb,Hc и Hd- ортоцентры
треугольников BCD,CDA,DAB и ABC. Прямые la,lb,lc и ld
проходят через середины отрезков AHa,BHb,CHc и DHd (см.
задачу 5.107). Середины этих отрезков совпадают с такой точкой H, что
| 2 |
®
OH
|
= |
®
OA
|
+ |
®
OB
|
+ |
®
OC
|
+ |
®
OD
|
|
, где
O — центр окружности (см. задачу 13.33).
-
5.109.
-
а) Пусть B1,C1 и D1- проекции точки P на
прямые AB,AC и AD. Точки B1,C1 и D1 лежат на окружности с
диаметром AP. Прямые B1C1,C1D1 и D1B1 являются прямыми
Симсона точки P относительно треугольников ABC,ACD и ADB
соответственно. Поэтому проекции точки P на прямые Симсона этих
треугольников лежат на одной прямой — прямой Симсона
треугольника B1C1D1. Аналогично доказывается, что на одной прямой
лежит любая тройка рассматриваемых точек.
б) Пусть P — точка описанной окружности n-угольника
A1… An; B2,B3,…, Bn- проекции точки P на
прямые A1A2,…,A1An. Точки B2,…,Bn лежат на окружности
с диаметром A1P. Докажем по индукции, что прямая Симсона точки P
относительно n-угольника A1… An совпадает с прямой Симсона
точки P относительно (n – 1)-угольника B2… Bn (для n = 4
это было доказано в задаче а). По предложению индукции прямая Симсона
(n – 1)-угольника A1A3… An совпадает с прямой Симсона
(n – 2)-угольника B3… Bn. Поэтому проекции точки P на
прямые Симсона (n – 1)-угольников, вершины которых получаются
последовательным исключением точек A2,…,An из
набора A1,…,An, лежат на прямой Симсона (n – 1)-угольника
B2… Bn. А проекция точки P на прямую Симсона (n – 1)-угольника
A2… An лежит на той же прямой потому, что наши рассуждения
показывают, что любые n – 1 из рассматриваемых n точек проекций лежат
на одной прямой.
-
5.110.
-
Точки B1 и C1 лежат на окружности с диаметром AP.
Поэтому B1C1 = APsin B1AC1 = AP(BC/2R).
-
5.111.
-
Эта задача является частным случаем задачи 2.44.
-
5.112.
-
Ясно, что РC1AP = РC1B1P = РA2B1P = РA2C2P = РB3C2P = РB3A3P (первое, третье и
пятое равенства получаются из вписанности соответствующих
четырехугольников; остальные равенства очевидны). Аналогично РB1AP = РC3A3P. Поэтому РB3A3C3 = РB3A3P + РC3A3P = РC1AP + РB1AP = РBAC. Аналогично получаются
равенства остальных углов треугольников ABC и A3B3C3.
-
5.113.
-
Пусть A1,B1 и C1- основания перпендикуляров,
опущенных из точки P на прямые BC,CA и AB; A2,B2 и C2
- точки пересечения прямых PA,PB и PC с описанной окружностью
треугольника ABC. Пусть далее S,S1 и S2- площади
треугольников ABC,A1B1C1 и A2B2C2. Легко проверить,
что a1 = a · AP/2R (задача 5.110) и a2 = a · B2P/CP.
Треугольники A1B1C1 и A2B2C2 подобны (задача 5.111),
поэтому S1/S2 = k2, где k = a1/a2 = AP · CP/(2R · B2P). А
так как B2P · BP = |d2 – R2|, то S1/S2 = (AP · BP · CP)2/4R2(d2 – R2)2. Треугольники A2B2C2 и ABC вписаны в
одну окружность, поэтому S2/S = a2b2c2/abc (см. задачу 12.1).
Ясно также, что, например, a2/a = B2P/CP = |d2 – R2|/(BP · CP).
Следовательно, S2 : S = |d2 – R2|3 : (AP · BP · CP)2.
Поэтому S1/S = (S1/S2)(S2/S) = |d2 – R2|/4R2.
-
5.114.
-
Точки B1 и C1 лежат на окружности с
диаметром PA, поэтому середина отрезка PA является центром
описанной окружности треугольника AB1C1. Следовательно,
la- серединный перпендикуляр к отрезку B1C1. Поэтому
прямые la,lb и lc проходят через центр описанной окружности
треугольника A1B1C1.
-
5.115.
-
а) Опустим из точек P1 и P2
перпендикуляры P1B1
и P2B2 на AC
и перпендикуляры P1C1
и P2C2 на AB. Докажем, что
точки B1,B2,C1 и C2 лежат на
одной окружности. В самом деле,
РP1B1C1 = РP1AC1 = РP2AB2 = РP2C2B2, а так как РP1B1A = РP2C2A, то РC1B1A = РB2C2A. Центр
окружности, на которой лежат указанные точки, является точкой
пересечения серединных перпендикуляров к отрезкам B1B2 и C1C2,
а оба эти перпендикуляра проходят через середину O отрезка P1P2,
т. е. O — центр этой окружности. В частности, точки B1 и C1
равноудалены от точки O. Аналогично точки A1 и B1 равноудалены
от точки O, т. е. O — центр описанной окружности
треугольника A1B1C1. Кроме того, OB1 = OB2.
б) Предыдущее доказательство проходит почти без изменений и в этом
случае.
-
5.116.
-
Пусть A1,B1 и C1- середины сторон BC,CA
и AB. Треугольники A1B1C1 и ABC подобны, причем коэффициент
подобия равен 2. Высоты треугольника A1B1C1 пересекаются в
точке O, поэтому OA1 : HA = 1 : 2. Пусть Mў- точка
пересечения отрезков OH и AA1.
Тогда OMў : MўH = OA1 : HA = 1 : 2
и AMў : MўA1 = OA1 : HA = 1 : 2,
т. е. Mў = M.
-
5.117.
-
Пусть A1,B1 и C1- середины сторон BC,CA
и AB; A2,B2 и C2- основания высот; A3,B3
и C3- середины отрезков, соединяющих точку пересечения высот с
вершинами. Так как A2C1 = C1A = A1B1 и A1A2||B1C1,
точка A2 лежит на описанной окружности треугольника A1B1C1.
Аналогично точки B2 и C2 лежат на описанной окружности
треугольника A1B1C1.
Рассмотрим теперь окружность S с диаметром A1A3. Так
как A1B3||CC2 и A3B3||AB, то РA1B3A3 = 90°, а значит, точка B3 лежит на окружности S.
Аналогично доказывается, что точки C1,B1 и C3 лежат на
окружности S. Окружность S проходит через вершины
треугольника A1B1C1, поэтому она является его описанной
окружностью.
При гомотетии с центром H и коэффициентом 1/2 описанная
окружность треугольника ABC переходит в описанную окружность
треугольника A3B3C3, т. е. в окружность девяти точек. Значит, при
этой гомотетии точка O переходит в центр окружности девяти точек.
-
5.118.
-
а) Докажем, например, что треугольники ABC и HBC
имеют общую окружность девяти точек. В самом деле, окружности
девяти точек обоих треугольников проходят через середину стороны BC
и середины отрезков BH и CH.
б) Прямая Эйлера проходит через центр окружности девяти
точек, а окружность девяти точек у этих треугольников общая.
в) Центром симметрии является центр окружности девяти точек
этих треугольников.
-
5.119.
-
Пусть AB > BC > CA. Легко проверить, что для
остроугольного и тупоугольного треугольников точка H пересечения высот
и центр O описанной окружности расположены именно так, как
на рис. 5.5 (т. е. для остроугольного треугольника точка O лежит
внутри треугольника BHC1, а для тупоугольного точки O и B лежат
по одну сторону от прямой CH). Поэтому в остроугольном
треугольнике прямая
Эйлера пересекает наибольшую сторону AB
и наименьшую сторону AC, а в тупоугольном треугольнике-
наибольшую сторону AB и среднюю по длине сторону BC.
-
5.120.
-
а) Пусть Oa,Ob и Oc- центры вневписанных
окружностей треугольника ABC. Вершины треугольника ABC являются
основаниями высот треугольника OaObOc (задача 5.2), поэтому
окружность девяти точек треугольника OaObOc проходит через
точки A,B и C.
б) Пусть O — точка пересечения высот треугольника OaObOc,
т. е. точка пересечения биссектрис треугольника ABC. Окружность
девяти точек треугольника OaObOc делит пополам отрезок OOa.
-
5.121.
-
Пусть AA1- высота, H — точка пересечения
высот. Согласно задаче 5.47, б) AH = 2R|cos A|. Медианы делятся
точкой их пересечения в отношении 1 : 2, поэтому прямая Эйлера
параллельна BC тогда и только тогда, когда AH : AA1 = 2 : 3
и векторы
и
сонаправлены,
т. е. 2Rcos A : 2Rsin Bsin C = 2 : 3.
Учитывая, что cos A = – cos (B + C) = sin B sin C – cos Bcos C, получаем sin Bsin C = 3cos Bcos C.
-
5.122.
-
Пусть CD — высота, O — центр описанной
окружности, N — середина стороны AB, а точка E делит пополам
отрезок, соединяющий C с точкой пересечения высот. Тогда CENO —
параллелограмм, поэтому РNED = РOCH = |РA – РB|
(см. задачу 2.90). Точки N,E и D лежат на окружности девяти точек,
поэтому отрезок ND виден из ее центра под углом 2РNED = 2|РA – РB|.
-
5.123.
-
Пусть O и I — центры описанной и вписанной
окружностей треугольника ABC, H — точка пересечения высот;
прямые AI и BI пересекают описанную окружность в точках A1
и B1. Предположим, что треугольник ABC не равнобедренный. Тогда
OI : IH = OA1 : AH и OI : IH = OB1 : BH. Так
как OB1 = OA1, то AH = BH, а значит, AC = BC. Приходим к
противоречию.
-
5.124.
-
Пусть O и I — центры описанной и вписанной
окружностей треугольника ABC, H — ортоцентр
треугольника A1B1C1. Проведем в треугольнике A1B1C1
высоты A1A2,B1B2 и C1C2. Треугольник A1B1C1
остроугольный (например, РB1A1C1 = (РB + РC)/2 < 90°), поэтому H — центр вписанной окружности
треугольника A2B2C2 (см. задачу 1.57, а)). Стороны
треугольников ABC и A2B2C2 параллельны (см. задачу 1.55, а)),
поэтому существует гомотетия, переводящая треугольник ABC
в A2B2C2. При этой гомотетии точка O переходит в точку I, а
точка I — в точку H, поэтому прямая IH проходит через
точку O.
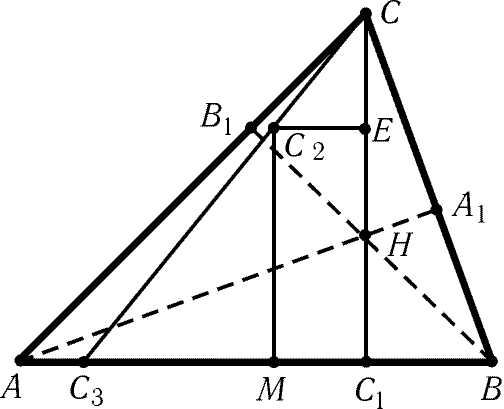
Рис. 5.6
5.125. Пусть H — точка пересечения высот
треугольника ABC, E и M — середины отрезков CH и AB
(рис. 5.6). Тогда C1MC2E — прямоугольник. Пусть прямая CC2
пересекает прямую AB в точке C3. Докажем,
что
|
AC3
|
: |
C3B
|
= tg 2a : tg 2b
|
. Легко
проверить, что
,
,
|
MC2
|
= |
C1E
|
= 2Rsin asin b – Rcos g
|
и
, поэтому
|
|
C3M
|
= Rsin (b – a)(2sin bsin a – cos g)/cos g = |
|
|
= Rsin (b – a)cos (b – a)/cos g. |
|
Следовательно,
|
|
|
= |
|
= |
sin 2g + sin (a – b)
sin 2g – sin (a – b)
|
= |
tg 2a
tg 2b
|
. |
|
Аналогичные рассуждения показывают, что
|
|
|
· |
A3C
|
· |
B3A
|
= |
tg 2a
tg 2b
|
· |
tg 2b
tg 2g
|
· |
tg 2g
tg 2a
|
= 1. |
|
-
5.126.
-
Решим сразу задачу б). Докажем сначала, что
прямые AA1,BB1 и CC1 пересекаются в одной точке. Пусть
описанные окружности треугольников A1BC и AB1C пересекаются в
точке O. Тогда Р(BO,OA) = Р(BO,OC) + Р(OC,OA) = Р(BA1,A1C) + Р(CB1,B1A) = Р(BA,AC1) + Р(C1B,BA) = Р(C1B,AC1), т. е. описанная окружность
треугольника ABC1 тоже проходит через точку O. Поэтому
Р(AO,OA1) = Р(AO,OB) + Р(BO,OA1) = Р(AC1,C1B) + Р(BC,CA1) = 0°, т. е. прямая AA1
проходит через точку O. Аналогично доказывается, что прямые BB1
и CC1 проходят через точку O.
Докажем теперь, что точка O совпадает с искомой точкой P.
Так как РBAP = РA – РCAP, то равенство РABP = РCAP эквивалентно равенству РBAP + РABP = РA, т. е. РAPB = РB + РC. Для точки O последнее
равенство очевидно, так как она лежит на описанной окружности
треугольника ABC1.
-
5.127.
-
а) Докажем, что ИAB = ИB1C1,
т. е. AB = B1C1. В самом деле, ИAB = ИAC1 + ИC1B,
а ИC1B = ИAB1, поэтому ИAB = ИAC1 + И
AB1 = ИB1C1.
б) Будем считать, что треугольники ABC и A1B1C1 вписаны
в одну окружность, причем треугольник ABC фиксирован, а
треугольник A1B1C1 вращается. Прямые AA1,BB1 и CC1
пересекаются в одной точке не более чем при одном положении
треугольника A1B1C1 (задача 7.20, б)). При этом может возникнуть 12
различных семейств треугольников A1B1C1: треугольники ABC
и A1B1C1 могут совмещаться поворотом или осевой симметрией; кроме
того, вершинам треугольника символы A1,B1 и C1 можно сопоставить
шестью различными способами.
Из этих 12 семейств треугольников четыре семейства никогда
не могут дать искомой точки P. Для одинаково ориентированных
треугольников исключаются случаи DABC = DA1B1C1,DABC = DC1B1A1
и DABC = DB1A1C1 (например, в
случае DABC = DA1C1B1 точка P является точкой
пересечения прямой BC = B1C1 и касательной к окружности в
точке A = A1; треугольники ABC и A1B1C1 при этом совпадают).
Для противоположно ориентированных треугольников исключается
случай DABC = DA1B1C1 (в этом случае AA1||
BB1||CC1).
Замечание.
Точкам Брокара соответствуют противоположно ориентированные
треугольники; для первой точки Брокара DABC = D
B1C1A1, а для второй точки Брокара DABC = D
C1A1B1.
-
5.128.
-
а) Так как
и
, то
|
sin jsin b
sin g
|
= |
sin (b – j)sin a
sin b
|
|
.
Учитывая, что sin (b – j) = sin bcos j – cos bsin j,
получаем
| ctg j
= ctg b + |
sin b
sin asin g
|
|
. Остается
заметить, что sin b
= sin (a + g) = sin acos g + sin gcos a.
б) Для второго угла Брокара получаем точно такое же выражение, как и в
задаче а). Ясно также, что оба угла Брокара острые.
в) Так как РA1BC = РBCA и РBCA1 = РCAB,
то DCA1B ~ DABC. Поэтому точка Брокара P лежит
на отрезке AA1 (см. задачу 5.126, б)).
-
5.129.
-
а) Согласно задаче 10.38,
a) ctg j
= ctg a + ctg b + ctg g і Ц3 = ctg 30°,
поэтому j Ј 30°.
б) Пусть P — первая точка Брокара треугольника ABC. Точка M
лежит внутри (или на границе) одного из треугольников ABP,BCP
и CAP. Если, например, точка M лежит внутри треугольника ABP,
то РABM Ј РABP Ј 30°.
-
5.130.
-
Прямые A1B1,B1C1 и C1A1 являются серединными
перпендикулярами к отрезкам AQ,BQ и CQ. Поэтому, например,
РB1A1C1 = 180° – РAQC = РA. Для других углов
доказательство аналогично.
Кроме того, прямые A1O,B1O и C1O являются серединными
перпендикулярами к отрезкам CA,AB и BC. Поэтому, например,
острые углы OA1C1 и ACQ имеют взаимно перпендикулярные
стороны, поэтому они равны. Аналогичные рассуждения показывают,
что РOA1C1 = РOB1A1 = РOC1B1 = j,
где j- угол Брокара треугольника ABC.
-
5.131.
-
По теореме синусов R1 = AB/2sin APB,R2 = BC/2sin BPC и R3 = CA/2sin CPA. Ясно также, что sin APB = sin A, sin BPC = sin B и sin CPA = sin C.
-
5.132.
-
Треугольник ABC1 равнобедренный, причем угол при его
основании AB равен углу Брокара j.
Поэтому Р(PC1,C1Q) = Р(BC1,C1A) = 2j.
Аналогично Р(PA1,A1Q) = Р(PB1,B1Q) = Р(PC1,C1Q) = 2j.
-
5.133.
-
Так как РCA1B1 = РA + РAB1A1
и РAB1A1 = РCA1C1, то РB1A1C1 = РA.
Аналогично доказывается, что равны и остальные углы треугольников ABC
и A1B1C1.
Описанные окружности треугольников AA1B1,BB1C1 и CC1A1
пересекаются в одной точке O (задача 2.81, а)). Ясно, что РAOA1 = РAB1A1 = j. Аналогично РBOB1 = РCOC1 = j. Поэтому РAOB = РA1OB1 = 180° – РA.
Аналогично РBOC = 180° – РB
и РCOA = 180° – РC, т. е. O — первая точка
Брокара обоих треугольников. Следовательно, при поворотной гомотетии
на угол j с центром O и коэффициентом AO/A1O
треугольник A1B1C1 переходит в треугольник ABC.
-
5.134.
-
а) Рассмотрим функцию f(x) = ln(x/sin x) = lnx – lnsin x. Ясно, что функции
|
fў(x) = |
1
x
|
– ctg x и fўў(x) = |
1
sin 2x
|
– |
1
x2
|
|
|
положительны при 0 < x < p. Следовательно, функция f(x) монотонно
возрастает при возрастании x от 0 до p и, кроме того, выпукла на этом
отрезке, т. е.
|
f(l1x1 + … + lnxn) Ј l1f(x1) + … + lnf(xn) |
|
при 0 Ј xi Ј p, 0 Ј li, l1 + ј + ln = 1. В
частности, f(j) Ј f(p/6), так как j Ј p/6, и
|
f(p/6) = f |
ж
и
|
j + (a – j) + j + (b – j) + j + (g – j)
6
|
ц
ш
|
Ј |
|
|
Ј |
1
6
|
|
ж
и
|
f(j) + f(a – j) + f(j) + f(b – j) + f(j) + f(g – j) |
ц
ш
|
. |
|
Воспользовавшись монотонностью логарифма, эти неравенства можно переписать
следующим образом:
|
|
ж
и
|
j
sin j
|
ц
ш
|
6
|
Ј |
ж
и
|
p/6
sin (p/6)
|
ц
ш
|
6
|
Ј |
j3(a – j)(b – j)(g – j)
sin 3jsin (a – j)sin (b – j)sin (g – j)
|
. |
|
Учитывая, что
sin (a – j)sin (b – j)sin (g – j) = sin 3j,
получаем
|
j3 Ј (a – j)(b – j)(g – j). |
|
б) Из неравенства
j3 Ј (a – j)(b – j)(g – j)
следует, что
|
64j6 Ј 43j(a – j)j(b – j)j(g – j). |
|
Ясно также, что
|
4j(a – j) Ј a2, 4j(b – j) Ј b2, 4j(g – j) Ј g2. |
|
-
5.135.
-
Согласно задаче 12.44, а)
|
ctg j = |
a2 + b2 + c2
4S
|
, |
|
где S - площадь треугольника. Таким образом, для треугольника с вершинами
в точках с координатами
(±a/2,0) и (x,y) угол Брокара j определяется равенством
|
ctg j = |
a2 + (a/2 + x)2 + y2 + ( – a/2 + x)2 + y2
2ay
|
, |
|
т. е. 2x2 + 2y2 + 3a2/4 = 2ayctg j.
Последнее уравнение задает окружность радиуса
с центром (0,(a/2)ctg j).
-
5.136.
-
Пусть a1,b1,c1 - длины сторон
треугольника A1B1C1, S1 - его площадь. В теореме речь идет о
множестве точек M, для которых выполняется равенство
|
4S1ctg j = a21 + b12 + c12. |
|
Точки B1 и C1 лежат на окружности с диаметром AM, поэтому
|
a1 = B1C1 = AMsin B1AC1 = |
aAM
2R
|
, |
|
где R - радиус описанной окружности треугольника ABC. Таким образом,
|
a21 + b12 + c12 = |
a2AM2 + b2BM2 + c2CM2
4R2
|
. |
|
Поэтому если (x,y) - координаты точки M в некоторой прямоугольной
системе координат, то
|
a21 + b12 + c12 = |
a2 + b2 + c2
4R2
|
(x2 + y2) + px + qy + r, |
|
где p,q,r - постоянные числа.
Для S1 тоже можно получить выражение через координаты (x,y) точки M.
При этом начало системы координат удобно расположить в центре O описанной
окружности треугольника ABC. В таком случае
|
S1 = |
SABC
4R2
|
|R2 – x2 – y2| |
|
(задача 5.113).
Уравнение S1 = 0 определяет описанную окружность треугольника ABC. Это
множество соответствует нулевому углу Брокара. Углу Брокара j
соответствует множество
|
±ctg j |
SABC
4R2
|
(R2 – x2 – y2) = |
a2 + b2 + c2
4R2
|
(x2 + y2) + px + qy + r. |
|
При этом знак плюс берется для точек внутри описанной
окружности, а знак минус берется для точек вне описанной
окружности. Легко видеть, что каждое из полученных уравнений
является уравнением окружности. Дело в том, что если f = 0 и
g = 0 - уравнения окружностей, то lf = g - тоже
уравнение окружности. Более того, центр окружности lf = g
лежит на прямой, соединяющей центры окружностей f = 0 и g = 0. В
нашем случае центром одной окружности служит центр описанной
окружности треугольника ABC, а центром второй окружности
служит точка, для которой величина a2AM2 + b2BM2 + c2CM2
минимальна (точка Лемуана).
-
5.137.
-
По теореме синусов AB/BM = sin AMB/sin BAM
и AB/BN = sin ANB/sin BAN. Значит,
|
|
AB2
BM · BN
|
= |
sin AMBsin ANB
sin BAMsin BAN
|
= |
sin AMCsin ANC
sin CANsin CAM
|
= |
AC2
CM · CN
|
. |
|
-
5.138.
-
Так как РBAS = РCAM,
то BS/CM = SBAS/SCAM = AB · AS/(AC · AM),
т. е. AS/AM = 2b · BS/ac.
Остается заметить, что BS = ac2/(b2 + c2)
и
(см. задачи 5.137 и 12.11, а)).
-
5.139.
-
При симметрии относительно биссектрисы угла A
отрезок B1C1 переходит в отрезок, параллельный стороне BC, а
прямая AS — в прямую AM, где M — середина стороны BC.
-
5.140.
-
Возьмем на отрезках BC и BA точки A1 и C1
так, что A1C1||BK. Так как РBAC = РCBK = РBA1C1
и РBCA = РBC1A1, то отрезок A1C1 антипараллелен
стороне AC. С другой стороны, согласно задаче 3.31, б) прямая BD
делит отрезок A1C1 пополам.
-
5.141.
-
Достаточно воспользоваться результатом задачи 3.30.
-
5.142.
-
Пусть AP — общая хорда рассматриваемых окружностей,
Q — точка пересечения прямых AP и BC.
Тогда BQ/AB = sin BAQ/sin AQB и AC/CQ = sin AQC/sin CAQ. Значит,
BQ/CQ = ABsin BAP/ACsin CAP. Так как AC и AB — касательные
к окружностям S1 и S2, то РCAP = РABP
и РBAP = РACP, а значит, РAPB = РAPC. Поэтому
|
|
AB
AC
|
= |
AB
AP
|
· |
AP
AC
|
= |
sin APB
sin ABP
|
· |
sin ACP
sin APC
|
= |
sin ACP
sin ABP
|
= |
sin BAP
sin CAP
|
. |
|
Следовательно, BQ/CQ = AB2/AC2.
-
5.143.
-
Пусть S — точка пересечения прямых AX и BC.
Тогда AS/AB = CS/CX и AS/AC = BS/BX, а значит,
CS/BS = (AC/AB) · (XC/XB). Остается заметить, что XC/XB = AC/AB
(см. решение задачи 7.16, а)).
-
5.144.
-
Пусть L,M и N — середины отрезков CA,CB и CH.
Так как DBAC ~ DCAH,
то DBAM ~ DCAN,
а значит, РBAM = РCAN.
Аналогично РABL = РCBN.
-
5.145.
-
Пусть B1C1,C2A2 и A3B3- данные отрезки.
Тогда треугольники A2XA3,B1XB3 и C1XC2 равнобедренные; пусть
длины их боковых сторон равны a,b и c. Прямая AX делит
отрезок B1C1 пополам тогда и только тогда, когда эта прямая
содержит симедиану. Поэтому если X — точка Лемуана, то a = b,b = c
и c = a. А если B1C1 = C2A2 = A3B3, то b + c = c + a = a + b, а значит,
a = b = c.
-
5.146.
-
Пусть M — точка пересечения медиан
треугольника ABC; a1,b1,c1 и a2,b2,c2- расстояния от
точек K и M до сторон треугольника. Так как точки K и M
изогонально сопряжены, то a1a2 = b1b2 = c1c2; кроме того,
aa2 = bb2 = cc2 (см. задачу 4.1). Следовательно,
a/a1 = b/b1 = c/c1. Используя это равенство и учитывая, что площади
треугольников A1B1K, B1C1K и C1A1K равны a1b1c/4R,b1c1a/4R и c1a1b/4R, где R — радиус описанной окружности
треугольника ABC, получаем, что площади этих треугольников равны.
Кроме того, точка K лежит внутри треугольника A1B1C1.
Следовательно, K — точка пересечения медиан
треугольника A1B1C1 (см. задачу 4.2).
-
5.147.
-
Медианы треугольника A1B1C1 пересекаются в
точке K (задача 5.146), поэтому стороны треугольника ABC
перпендикулярны медианам треугольника A1B1C1. После поворота
на 90° стороны треугольника ABC станут параллельны медианам
треугольника A1B1C1, а значит, медианы треугольника ABC станут
параллельны сторонам треугольника A1B1C1 (см. задачу 13.2).
Поэтому медианы треугольника ABC перпендикулярны сторонам
треугольника A1B1C1.
-
5.148.
-
Пусть A2,B2 и C2- проекции точки K на
прямые BC,CA и AB. Тогда DA1B1C1 ~ D
A2B2C2 (задача 5.111) и K — точка пересечения медиан
треугольника A2B2C2 (задача 5.146). Поэтому преобразование
подобия, переводящее треугольник A2B2C2 в треугольник A1B1C1,
переводит точку K в точку M пересечения медиан
треугольника A1B1C1. Кроме того, например, РKA2C2 = РKBC2 = РB1A1K, т. е. точки K и M изогонально
сопряжены относительно треугольника A1B1C1, а значит,
K — точка Лемуана треугольника A1B1C1.
5.149. Пусть K — точка Лемуана треугольника ABC;
A1,B1 и C1- проекции точки K на стороны
треугольника ABC; L — середина отрезка B1C1; N —
точка пересечения прямой KL и медианы AM; O — середина
отрезка AK (рис. 5.7).
Точки B1 и C1 лежат на окружности с
диаметром AK, поэтому согласно
задаче 5.146 OL^B1C1.
Кроме
того, AN^B1C1
(задача 5.147) и O — середина
отрезка AK, а значит, OL — средняя линия треугольника AKN
и KL = LN. Следовательно, K — середина отрезка A1N. Остается
заметить, что при гомотетии с центром M, переводящей N в A,
отрезок NA1 переходит в высоту AH.

 Глава 5. Задачи для самостоятельного решения |
Глава 5. Задачи для самостоятельного решения | 

 Глава 5. Задачи для самостоятельного решения |
Глава 5. Задачи для самостоятельного решения | 

