| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
6.1.
-
Пусть O — центр вписанной окружности и точка
пересечения диагоналей четырехугольника ABCD. Тогда РACB = РACD и РBAC = РCAD. Поэтому треугольники ABC
и ADC равны, так как сторона AC у них общая. Следовательно,
AB = DA. Аналогично AB = BC = CD = DA.
-
6.2.
-
Ясно, что РAOB = 180° – РBAO – РABO = 180° – (РA + РB)/2 и РCOD = 180° – (РC + РD)/2. Следовательно,
РAOB + РCOD = 360° – (РA + РB + РC + РD)/2 = 180°.
-
6.3.
-
Рассмотрим две окружности, касающиеся сторон данного
четырехугольника и их продолжений. Прямые, содержащие стороны
четырехугольника, являются общими внутренними и внешними
касательными к этим окружностям. Прямая, соединяющая центры
окружностей, содержит диагональ четырехугольника, и, кроме того,
она является осью симметрии четырехугольника. Значит, вторая
диагональ перпендикулярна этой прямой.
-
6.4.
-
Пусть O — центр данной окружности, R — ее
радиус, a — длина хорд, высекаемых окружностью на сторонах
четырехугольника. Тогда расстояния от точки O до сторон
четырехугольника равны
, т. е. она равноудалена от
сторон четырехугольника и является центром вписанной окружности.
-
6.5.
-
Для параллелограмма утверждение задачи очевидно, поэтому
можно считать, что прямые AB и CD пересекаются. Пусть O —
центр вписанной окружности четырехугольника ABCD; M и N —
середины диагоналей AC и BD. Тогда SANB + SCND = SAMB + SCMD = SAOB + SCOD = SABCD/2. Остается воспользоваться
результатом задачи 7.2.
-
6.6.
-
Пусть вписанная окружность касается сторон DA,AB и BC
в точках M,H и N соответственно. Тогда OH — высота
треугольника AOB и при симметрии относительно прямых AO и BO
точка H переходит в точки M и N соответственно. Поэтому согласно
задаче 1.58 точки A1 и B1 лежат на прямой MN. Аналогично
точки C1 и D1 лежат на прямой MN.
-
6.7.
-
Пусть r — расстояние от точки пересечения биссектрис
углов A и D до основания AD, rў расстояние от точки
пересечения биссектрис углов B и C до основания BC.
Тогда AD = r(ctg a + ctg b) и BC = rў(tg a + tg b). Поэтому r = rў
тогда и только тогда, когда BC/AD = (tg a + tg b)/(ctg a + ctg b) = tg a · tg b.
-
6.8.
-
Пусть РA = 2a,
РC = 2b
и РBMA = 2j.
Согласно задаче 6.7 PK/RL = tg atg j
и LS/MC = ctg jtg b. Так как PQ/RS = PK/RL и RS/AC = LS/MC,
то PQ/AC = (PK/RL)(LS/MC) = tg atg b. Следовательно, трапеция APQC
описанная.
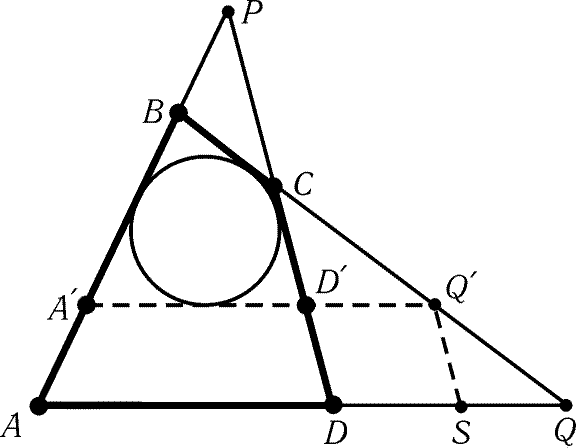
Рис. 6.4
6.9. Докажем сначала, что если четырехугольник ABCD
описанный, то выполняются все условия. Пусть K,L,M и N —
точки касания вписанной окружности со сторонами AB,BC,CD и DA.
Тогда AB + CD = AK + BK + CM + DM = AN + BL + CL + DN = BC + AD,AP + CQ = AK + PK + QL – CL = AN + PM + QN – CM = AQ + CP
и BP + BQ = AP – AB + BC + CQ = (AP + CQ) + (BC – AB) = AQ + CP + CD – AD = DP + DQ.
Докажем теперь, например, что если BP + BQ = DP + DQ, то
четырехугольник ABCD описанный. Рассмотрим для этого окружность,
касающуюся стороны BC и лучей BA и CD. Предположим, что
прямая AD не касается этой окружности; сдвинем эту прямую так, чтобы
она коснулась окружности (рис. 6.4). Пусть S — такая точка
прямой AQ, что QўS||DDў. Так как BP + BQ = DP + DQ
и BP + BQў = DўP + DўQў, то QS + SQў = QQў. Получено противоречие. В двух
других случаях доказательство проводится аналогично.
-
6.10.
-
Пусть лучи AB и DC пересекаются в точке P,
лучи BC и AD — в точке Q; данные прямые, проходящие через
точки P и Q, пересекаются в точке O. Согласно задаче 6.9
BP + BQ = OP + OQ и OP + OQ = DP + DQ. Следовательно, BP + BQ = DP + DQ, а
значит, четырехугольник ABCD описанный.
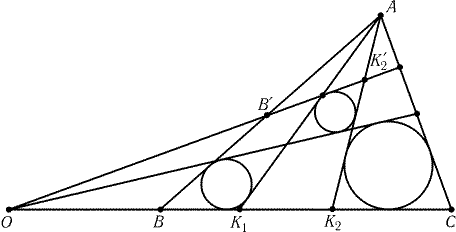
Рис. 6.5
6.11.
Пусть O - точка пересечения общих внешних касательных к
вписанным окружностям треугольников ABK1 и ACK2 (рис. 6.5).
Проведем из точки O касательную l к вписанной окружности
треугольника, образованного прямыми AK1, AK2 и касательной
к вписанным окружностям треугольников ABK1 и ACK2,
отличной от прямой BC. Пусть прямая l пересекает прямые AB
и AK2 в точках Bў и K2ў. Согласно задаче 6.15
четырехугольник BK2K2ўBў описанный. Это означает, что прямая
l касается вписанной окружности треугольника ABK2.
Аналогично доказывается, что прямая l касается вписанной
окружности треугольника ACK1.
-
6.12.
-
а) Сопоставим окружности (x – a)2 + (y – b)2 = r2
с заданной на ней ориентацией (направлением обхода) точку с
координатами (a,b,±r), где знак перед r соответствует
ориентации окружности. Рассмотрим пару пересекающихся прямых, на
которых заданы ориентации (направления). Легко убедиться, что
семейству ориентированных окружностей, касающихся данных прямых
так, что в точках касания ориентации согласованы, сопоставляется
прямая в пространстве, проходящая через точку плоскости r = 0,
соответствующую точке пересечения двух данных прямых.
Пусть прямые AB и CD пересекаются в точке P, а прямые BC
и AD - в точке Q. Предположим, что четырехугольники,
примыкающие к вершинам A, B и C, описанные. Зададим на
вписанных в них окружностях ориентации согласованным образом и
перенесем эти ориентации на касательные. Пусть этим
ориентированным окружностям соответствуют точки Oa, Ob и
Oc. Тогда точки Oa, Ob и P лежат на одной прямой;
точки Ob, Oc и Q тоже лежат на одной прямой.
Следовательно, все эти точки лежат в одной плоскости. Поэтому
прямые OaQ и OcP пересекаются в некоторой точке Od.
(Вообще говоря, эти прямые могли бы быть параллельны. Чтобы
исключить такую возможность, нужно воспользоваться тем, что
если, например, точка B лежит между A и P, то точка Ob
лежит между Oa и P.) Точке Od соответствует окружность,
вписанная в четырехугольник, примыкающий к вершине D.
б) Радиусы ra, rb, rc, rd пропорциональны
расстояниям от точек Oa, Ob, Oc, Od до прямой PQ.
Поэтому нужно лишь воспользоваться результатом задачи 1.3, б).
-
6.13.
-
На окружностях и касательных можно выбрать
ориентации согласованным образом (рис. 6.6). Пусть Ai -
точка пересечения касательных к окружности Si. Ориентации
касательных задают ориентацию четырехугольника A1A2A3A4
(этот четырехугольник может быть невыпуклым). Из равенства длин
касательных, проведенных из точки Ai к окружности Si,
следует, что
|
A1A2 + A3A4 = A2A3 + A1A4. |
| (1) |
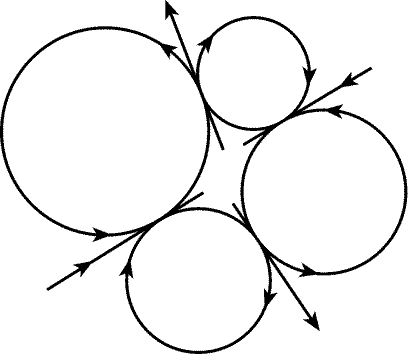
Рис. 6.6
Воспользовавшись результатом задачи 6.9, получим, что стороны
четырехугольника A1A2A3A4 (или их продолжения) касаются
одной окружности, если только этот четырехугольник
невырожденный.
Если три касательные пересекаются в одной точке, то из
равенства (1) следует, что четырехугольник A1A2A3A4
вырождается в отрезок или в точку. В отрезок он вырождаться не
может, поскольку если две касательные сливаются в одну прямую
l, то они должны соответствовать противоположным сторонам
четырехугольника; в этом случае все касательные пересекаются в
одной точке (середине отрезка, высекаемого на прямой l точками
касания).
-
6.14.
-
Пусть стороны AB,BC,CD,DA четырехугольника ABCD
касаются вписанной окружности в точках E,F,G,H соответственно.
Покажем сначала, что прямые FH,EG и AC пересекаются в одной точке.
Обозначим точки, в которых прямые FH и EG пересекают прямую AC,
через M и Mў соответственно. Поскольку РAHM = РBFM как
углы между касательными и хордой HF, то sin AHM = sin CFM.
Поэтому
|
AM · MH
FM · MC
|
= |
SAMH
SFMC
|
= |
AH · MH
FC · FM
|
|
,
т. е.
Аналогично
|
AMў
MўC
|
= |
AE
CG
|
= |
AH
FC
|
= |
AM
MC
|
|
,
поэтому M = Mў, т. е. прямые FH,EG и AC пересекаются в одной точке.
Аналогичные рассуждения показывают, что прямые FH,EG и BD
пересекаются в одной точке, поэтому прямые AC,BD,FH и EG
пересекаются в одной точке.
-
6.15.
-
Отрезки CHd и DHc параллельны, так как они
перпендикулярны прямой BC. Кроме того, так как РBCA = РBDA = j, длины этих отрезков равны AB|ctg j| (см.
задачу 5.47, б)).
-
6.16.
-
Пусть Oa,Ob,Oc и Od- центры вписанных
окружностей треугольников BCD,ACD,ABD и ABC соответственно. Так
как РADB = РACB,
то РAOcB = 90° + (РADB/2) = 90° + (РACB/2) = РAOdB (см. задачу 5.3).
Поэтому четырехугольник ABOdOc вписанный, т.е.
РOcOdB = 180° – РOcAB = 180° – (РA/2).
Аналогично РOaOdB = 180° – (РC/2). Так как РA + РC = 180°, то РOcOdB + РOaOdB = 270°, а значит, РOaOdOc = 90°.
Аналогично доказывается, что и остальные углы
четырехугольника OaObOcOd равны 90°.
-
6.17.
-
а) Пусть лучи AB и DC пересекаются в точке P, а
лучи BC и AD — в точке Q. Докажем, что точка M, в которой
пересекаются описанные окружности треугольников CBP и CDQ, лежит на
отрезке PQ. В самом деле, РCMP + РCMQ = РABC + РADC = 180°. Поэтому PM + QM = PQ, а так как PM · PQ = PD · PC = p2 – R2 и QM · PQ = QD · QA = q2 – R2, то PQ2 = PM · PQ + QM · PQ = p2 + q2 – 2R2.
Пусть N — точка пересечения описанных окружностей
треугольников ACP и ABS. Докажем, что точка S лежит на
отрезке PN. В самом деле, РANP = РACP = 180° – РACD = 180° – РABD = РANS.
Поэтому PN – SN = PS, а так как PN · PS = PA · PB = p2 – R2
и SN · PS = SA · SC = R2 – s2, то PS2 = PN · PS – SN · PS = p2 + s2 – 2R2. Аналогично QS2 = q2 + s2 – 2R2.
б) Согласно задаче а) PQ2 – PS2 = q2 – s2 = OQ2 – OS2. Следовательно,
OP^QS (см. задачу 7.6). Аналогично доказывается,
что OQ^PS и OS^PQ.
-
6.18.
-
Пусть вписанные окружности треугольников ABC и ACD
касаются диагонали AC в точках M и N соответственно.
Тогда AM = (AC + AB – BC)/2 и AN = (AC + AD – CD)/2 (см. задачу 3.2). Точки M
и N совпадают тогда и только тогда, когда AM = AN,
т. е. AB + CD = BC + AD. Итак, если точки M и N совпадают, то
четырехугольник ABCD описанный, и аналогичные рассуждения показывают,
что точки касания вписанных окружностей треугольников ABD и BCD с
диагональю BD совпадают.
Пусть вписанная окружность треугольника ABC касается сторон AB,BC
и CA в точках P,Q и M, а вписанная окружность треугольника ACD
касается сторон AC,CD и DA в точках M,R и S. Так как AP = AM = AS
и CQ = CM = CR, то треугольники APS,BPQ,CQR и DRS равнобедренные;
пусть a,b,g и d- углы при основаниях этих
равнобедренных треугольников. Сумма углов этих треугольников
равна 2(a + b + g + d) + РA + РB + РC + РD,
поэтому a + b + g + d
= 180°. Следовательно, РSPQ + РSRQ = 360° – (a + b + g + d) = 180°,
т. е. четырехугольник PQRS вписанный.
-
6.19.
-
Пусть O — точка пересечения диагоналей AC и BD;
A1,B1,C1 и D1- ее проекции на стороны AB,BC,CD и DA.
Точки A1 и D1 лежат на окружности с диаметром AO,
поэтому РOA1D1 = РOAD1. Аналогично РOA1B1 = РOBB1. А так как РCAD = РCBD, то РOA1D1 = РOA1B1. Аналогично доказывается, что B1O,C1O
и D1O — биссектрисы углов четырехугольника A1B1C1D1,
т. е. O — центр его вписанной окружности.
-
6.20.
-
Воспользуемся обозначениями рис. 6.7. Условие вписанности
четырехугольника A1B1C1D1 эквивалентно тому,
что (a + b) + (g + d) = 180°, а перпендикулярность
диагоналей AC и BD — тому,
что (a1 + d1) + (b1 + g1) = 180°. Ясно также,
что a
= a1, g
= g1 и d
= d1.
-
6.21.
-
По теореме косинусов AD2 = AC2 + CD2 – 2AC · CD · cos ACD и AC2 = AB2 + BC2 – 2AB · BCcos B. А так как длина
проекции отрезка AC на прямую l, перпендикулярную CD, равна сумме
длин проекций отрезков AB и BC на прямую l, то ACcos ACD = ABcos j + BCcos C.
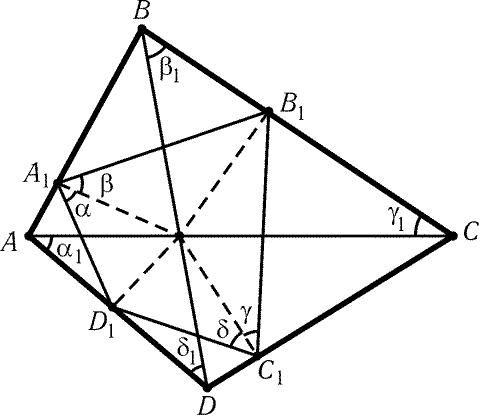
Рис. 6.7
6.22. Пусть РAOD = 2a. Тогда расстояния от точки O до
проекций середин диагоналей AC и BD на биссектрису угла AOD
равны cos a(OA + OC)/2 и cos a(OB + OD)/2 соответственно. Так
как OA + OC = AB + OB + OC = CD + OB + OC = OB + OD, эти проекции совпадают.
6.23. Достроим треугольники ABM и DCM до
параллелограммов ABMM1 и DCMM2. Так как AM1 :
DM2 = BM : MC = AN : DN, то DANM1 ~ D
DNM2. Поэтому точка N лежит на отрезке M1M2
и MM1 : MM2 = AB : CD = AN : ND = M1N : M2N,
т. е. MN — биссектриса угла M1MM2.
-
6.24.
-
Пусть a,b,c и d — биссектрисы углов при
вершинах A,B,C и D. Нужно проверить,
что Р(a,b) + Р(c,d) = 0°.
Ясно, что Р(a,b) = Р(a,AB) + Р(AB,b)
и Р(c,d) = Р(c,CD) + Р(CD,d). Так как
четырехугольник ABCD выпуклый и
Р(a,AB) = Р(AD,AB)/2,
Р(AB,b) = Р(AB,BC)/2,
Р(c,CD) = Р(CB,CD)/2,
Р(CD,d) = Р(CD,DA)/2, то
Р(a,b) + Р(c,d) = (Р(AD,AB) + Р(AB,BC) + Р(CB,CD) + Р(CD,DA))/2,Р(CD,d) = Р(CD,DA)/2 = 360°/2 = 0°.
(см. «Основные сведения» гл. 2).
-
6.25.
-
Пусть для определенности AB > A1B1. При параллельном
переносе на вектор
треугольник SD1C1 переходит
в SўD1ўC1ў, а отрезок CD переходит в BA. Так
как QA1 : QA = A1B1 : AB = SўD1ў : SўA,
то QSў||A1Dў1.
Следовательно, QS||AD.
Аналогично PR||AB.
-
6.26.
-
Предположим, что прямые AD и BC не параллельны.
Пусть M2,K,N2- середины сторон AB,BC,CD соответственно.
Если MN||BC, то BC||AD, так как AM = MC и BN = ND. Поэтому
будем считать, что прямые MN и BC не параллельны, т. е. M1 № M2
и N1 № N2. Ясно, что
и
. Поэтому M1M2||N1N2.
Следовательно, KM||AB||CD||KN, т. е. M = N. Получено
противоречие.
-
6.27.
-
Преобразованием подобия можно совместить одну пару
соответственных сторон четырехугольников, поэтому достаточно
рассмотреть четырехугольники ABCD и ABC1D1, у которых точки C1
и D1 лежат на лучах BC,AD и CD||C1D1. Обозначим точки
пересечения диагоналей четырехугольников ABCD и ABC1D1 через O
и O1 соответственно.
Предположим, что точки C и D лежат ближе к точкам B и A,
чем точки C1 и D1. Докажем, что тогда РAOB > РAO1B.
В самом деле, РC1BA > РCAB и РD1BA > РDBA,
поэтому РAO1B = 180° – РC1AB – РD1BA < 180° – РCAB – РDBA = РAOB. Получено
противоречие, поэтому C1 = C, D1 = D.
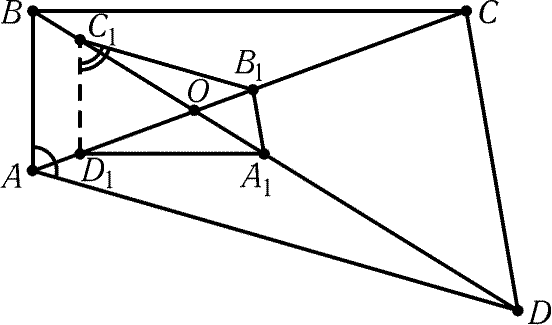
Рис. 6.8
6.28. Любой четырехугольник с точностью до подобия определяется
направлениями своих сторон и диагоналей, поэтому достаточно построить
один пример четырехугольника A1B1C1D1 с требуемыми направлениями
сторон и диагоналей. Пусть O — точка пересечения диагоналей AC
и BD. На луче OA возьмем произвольную точку D1 и
проведем D1A1||BC, A1B1||CD и B1C1||DA (рис. 6.8). Так
как OC1 : OB1 = OD : OA, OB1 : OA1 = OC : OD
и OA1 : OD1 = OB : OC, то OC1 : OD1 = OB : OA,
а значит, C1D1||AB. Из полученного рисунка ясно, что РA + РC1 = 180°.
-
6.29.
-
Пусть O — точка пересечения диагоналей
четырехугольника ABCD. Без ограничения общности можно считать,
что a
= РAOB < 90°. Опустим перпендикуляры AA1, BB1,CC1, DD1 на диагонали четырехугольника ABCD. Так
как OA1 = OAcos a, OB1 = OBcos a, OC1 = OCcos a, OD1 = ODcos a,
то при симметрии относительно биссектрисы угла AOB
четырехугольник ABCD переходит в четырехугольник, гомотетичный
четырехугольнику A1B1C1D1 (с коэффициентом 1/cos a).
-
6.30.
-
Пусть диагонали четырехугольника ABCD пересекаются в
точке O; Ha и Hb- ортоцентры треугольников AOB и COD;
Ka и Kb- середины сторон BC и AD; P — середина
диагонали AC. Точки пересечения медиан треугольников AOD и BOC
делят отрезки KaO и KbO в отношении 1 : 2, поэтому нужно
доказать, что HaHb^KaKb.
Так как OHa = AB|ctg j| и OHb = CD|ctg j|,
где j
= РAOB (см. задачу 5.47, б)), то OHa :
OHb = PKa : PKb. Соответственные стороны углов HaOHb
и KaPKb, перпендикулярны; кроме того, векторы
и
направлены к прямым AB и CD при j < 90° и
от этих прямых при j > 90°. Поэтому РHaOHb = РKaPKb и DHaOHb ~ DKaPKb. Следовательно,
HaHb^KaKb.
-
6.31.
-
Пусть S = SAOD, x = AO, y = DO, a = AB, b = BC, c = CD, d = DA;
k — коэффициент подобия треугольников BOC и AOD. Тогда
|
2 |
ж
и
|
1
r1
|
+ |
1
r3
|
ц
ш
|
= |
d + x + y
S
|
+ |
kd + kx + ky
k2S
|
, |
|
|
2 |
ж
и
|
1
r2
|
+ |
1
r4
|
ц
ш
|
= |
a + x + ky
kS
|
+ |
c + kx + y
kS
|
, |
|
так как SBOC = k2S и SAOB = SCOD = kS. Поскольку
|
|
x + y
S
|
+ |
x + y
k2S
|
= |
x + ky
kS
|
+ |
kx + y
kS
|
, |
|
остается заметить, что a + c = b + d = kd + d.
-
6.32.
-
Легко проверить, что AB = r1(ctg (A/2) + ctg (B/2))
и CD = r3(ctg (C/2) + ctg (D/2)). Поэтому
AB/r1 + CD/r3 = ctg (A/2) + ctg (B/2) + ctg (C/2) + ctg (D/2) = BC/r2 + AD/r4.
-
6.33.
-
Достроим треугольники ABD и DBC до
параллелограммов ABDA1 и DBCC1. Отрезки, соединяющие точку D с
вершинами параллелограмма ACC1A1, делят его на четыре треугольника,
равных треугольникам DAB, CDA, BCD и ABC, поэтому радиусы вписанных
окружностей этих треугольников равны. Докажем, что точка D
совпадает с точкой O пересечения диагоналей параллелограмма.
Если D № 0, то можно считать, что точка D лежит внутри
треугольника AOC. Тогда
rADC < rAOC = rA1OC1 < rA1DC1 = rABC (см. задачу 10.87).
Получено противоречие, поэтому D = O.
Так как p = S/r, а площади и радиусы вписанных окружностей
треугольников, на которые диагонали делят параллелограмм ACC1A1,
равны, то равны и их периметры. Поэтому ACC1A1- ромб, a ABCD
- прямоугольник.
-
6.34.
-
Точки C1 и D1 лежат на серединном перпендикуляре
к отрезку AB, поэтому AB^C1D1. Аналогично C1D1^A2B2, а значит, AB||A2B2. Аналогично доказывается, что
параллельны и остальные соответственные стороны и диагонали
четырехугольников ABCD и A2B2C2D2. Следовательно, эти
четырехугольники подобны.
Пусть M — середина отрезка AC. Тогда B1M = |AMctg D|
и D1M = |AMctg B|, причем B1D1 = |ctg B + ctg D| · AC/2. Повернем
четырехугольник A1B1C1D1 на 90°. Тогда, воспользовавшись
результатом задачи 6.28, получим, что этот четырехугольник выпуклый,
причем ctg A = – ctg C1 и т. д. Поэтому A2C2 = |ctg A + ctg C| · B1D1/2 = |(ctg A + ctg C)(ctg B + ctg D)/4| · AC.
-
6.35.
-
Пусть M и N — середины сторон AB и CD.
Опустим из точки D перпендикуляр DP на прямую MN, а из точки M
перпендикуляр MQ на CD. Тогда Q — точка касания прямой CD и
окружности с диаметром AB. Прямоугольные треугольники PDN и QMN
подобны, поэтому DP = ND · MQ/MN = ND · MA/MN. Аналогично
расстояние от точки A до прямой MN равно ND · MA/MN.
Следовательно, AD||MN. Аналогично BC||MN.
-
6.36.
-
Достаточно проверить, что ортоцентры любых трех из
данных четырех треугольников лежат на одной прямой. Пусть
некоторая прямая пересекает прямые B1C1, C1A1 и A1B1 в
точках A,B и C соответственно; A2,B2 и C2- ортоцентры
треугольников A1BC, AB1C и ABC1. Прямые AB2 и A2B
перпендикулярны прямой A1B1, поэтому они параллельны.
Аналогично BC2||B2C и CA2||C2A. Точки A,B и C лежат на
одной прямой, поэтому точки A2,B2 и C2 тоже лежат на одной
прямой (см. задачу 1.12, б)).
-
6.37.
-
Возьмем на диагонали BD точку M так,
что РMCD = РBCA.
Тогда DABC ~ DDMC, так как
углы BAC и BDC опираются на одну дугу. Поэтому AB · CD = AC · MD.
Поскольку РMCD = РBCA,
то РBCM = РACD
и DBCM ~ DACD,
так как углы CBD
и CAD опираются на одну дугу. Поэтому BC · AD = AC · BM.
Следовательно,
AB · CD + AD · BC = AC · MD + AC · BM = AC · BD.
-
6.38.
-
Пусть S — площадь четырехугольника ABCD,
R — радиус его описанной окружности.
Тогда S = SABC + SADC = AC(AB · BC + AD · DC)/4R (см.
задачу 12.1). Аналогично S = BD(AB · AD + BC · CD)/4R. Приравнивая
эти выражения для S, получаем требуемое.
-
6.39.
-
Пусть правильный семиугольник A1… A7 вписан в
окружность. Применяя теорему Птолемея к
четырехугольнику A1A3A4A5, получаем A1A3 · A5A4 + A3A4 · A1A5 = A1A4 · A3A5,
т. е. sin 2asin a + sin asin 3a
= sin 3asin 2a.
-
6.40.
-
Пусть A1,B1 и C1- середины сторон BC,CA
и AB. По теореме Птолемея AC1 · OB1 + AB1 · OC1 = AO · B1C1, где O — центр описанной окружности.
Поэтому cdb + bdc = aR. Аналогично adc + cda = bR и adb + bda = cR.
Кроме того, ada + bdb + cdc = 2S = (a + b + c)r. Складывая все эти равенства
и сокращая на a + b + c, получаем требуемое.
-
6.41.
-
По теореме Птолемея AB · CD + AC · BD = AD · BC.
Учитывая, что CD = BD і BC/2, получаем требуемое.
-
6.42.
-
Применяя теорему Птолемея к четырехугольнику ABCP
и сокращая на длину стороны квадрата, получаем требуемое.
-
6.43.
-
Применяя теорему Птолемея к четырехугольнику APQR,
получаем AP · RQ + AR · QP = AQ · PR. Так как РACB = РRAQ = РRPQ и РRQP = 180° – РPAR = РABC, то DRQP ~ DABC, а значит, RQ :
QP : PR = AB : BC : CA. Остается заметить, что BC = AD.
-
6.44.
-
а) Запишем теорему Птолемея для всех четырехугольников
с вершинами в точке A и трех последовательных вершинах данного
многоугольника; затем сгруппируем в полученных равенствах сомножители,
в которые входят di с четными номерами, в правую часть. Сложив эти
равенства, получим (2a + b)(d1 + … + d2n + 1) = (2a + b)(d2 + … + d2n), где a — сторона данного многоугольника,
b — его наименьшая диагональ.
б) Пусть R — радиус окружности S. Тогда
(см. задачу 3.20). Остается воспользоваться результатом
задачи а).
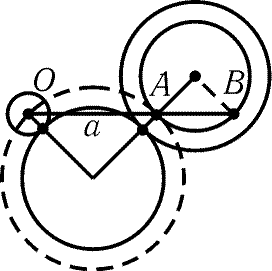
Рис. 6.9
6.45. Пусть оба касания внешние и x Ј y. Прямая,
проходящая через центр O окружности радиуса x параллельно отрезку,
соединяющему точки касания, пересекает окружность радиуса y – x (с
центром в центре окружности радиуса y) в точках A и B (рис. 6.9).
Тогда OA = a(R + x)/R и OB = OA + a(y – x)/R = a(R + y)/R. Квадрат искомой длины
общей внешней касательной равен
|
OA · OB = (a/R)2(R + x)(R + y). |
|
Аналогичные рассуждения показывают, что если оба касания внутренние, то
квадрат длины внешней касательной равен (a/R)2(R – x)(R – y), а если
окружность радиуса x касается внешне, а окружность радиуса y —
внутренне, то квадрат длины внутренней касательной
равен (a/R)2(R – y)(R + x).
Замечание.
В случае внутреннего касания окружностей предполагается, что R > x
и R > y.
-
6.46.
-
Пусть R — радиус описанной окружности
четырехугольника ABCD; ra, rb, rc
и rd- радиусы
окружностей a,b,g и d.
Пусть далее
,
причем знак плюс берется в случае внешнего касания, а знак минус- в
случае внутреннего; числа b,c и d определяются аналогично.
Тогда tab = ab AB/R (см. задачу 6.45) и т. д.
Поэтому, домножая равенство AB · CD + BC · DA = AC · BD
на abcd/R, получаем требуемое.
-
6.47.
-
Так как РEBD = РABE + РCBD, то на
стороне ED можно взять точку P так, что РEBP = РABE = РAEB, т. е. BP||AE. Тогда РPBD = РEBD – РEBP = РCBD = РBDC, т. е. BP||CD. Следовательно,
AE||CD, а так как AE = CD, то CDEA — параллелограмм.
Поэтому AC = ED, т. е. треугольник ABC равносторонний и РABC = 60°.
-
6.48.
-
а) Пусть O — центр описанной окружности
треугольника CKE. Достаточно проверить, что РCOK = 2РKCB.
Оба эти угла легко вычисляются: РCOK = 180° – 2РOKC = 180° – РEKC = 180° – РEDC = 72°
и РKCB = (180° – РABC)/2 = 36°.
б) Так как BC — касательная к описанной окружности
треугольника CKE, то BE · BK = BC2, т. е. d(d – a) = a2.
-
6.49.
-
Пусть перпендикуляры, восставленные к прямой AB в
точках A и B, пересекают стороны DE и CD в точках P и Q.
Любая точка отрезка CQ является вершиной прямоугольника, вписанного в
пятиугольник ABCDE (стороны этого прямоугольника параллельны AB
и AP), причем при перемещении этой точки от Q к C отношение длин
сторон прямоугольников изменяется от AP/AB до 0. Так как угол AEP
тупой, то AP > AE = AB. Поэтому для некоторой точки отрезка QC отношение
длин сторон прямоугольника равно 1.
-
6.50.
-
Пусть точки A1,…,E1 симметричны
точкам A,…,E относительно центра окружности S; P,Q и R —
точки пересечения прямых BC1 и AB1, AE1 и BA1, BA1
и CB1 (рис. 6.10). Тогда PQ = AB = a и QR = b. Так как PQ||AB
и РABA1 = 90°, то PR2 = PQ2 + QR2 = a2 + b2. Прямая PR
проходит через центр окружности S и РAB1C = 4 · 18° = 72°, поэтому PR — сторона
правильного пятиугольника, описанного около окружности с центром B1,
радиус B1O которой равен радиусу окружности S.
-
6.51.
-
Проведем через точки A,C и E прямые l1,l2
и l3, параллельные прямым BC,DE и FA соответственно. Обозначим
точки пересечения прямых l1 и l2, l2 и l3, l3 и l1
через P,Q,R соответственно (рис. 6.11). Тогда
|
SACE = (SABCDEF – SPQR)/2 + SPQR = (SABCDEF + SPQR)/2 і SABCDEF/2. |
|
Аналогично SBDF = (SABCDEF + SPўQўRў)/2. Ясно, что
PQ = |AB – DE|, QR = |CD – AF|, PR = |EF – BC|,
поэтому треугольники PQR и PўQўRў равны. Следовательно,
SACE = SBDF.
-
6.52.
-
Построим треугольник PQR, как и в предыдущей задаче.
Этот треугольник правильный, и
PQ = |AB – DE|, QR = |CD – AF|, PR = |EF – BC|.
Поэтому |AB – DE| = |CD – AF| = |EF – BC|.
-
6.53.
-
Сумма углов при вершинах A,C и E
равна 360°, поэтому из равнобедренных треугольников ABF,CBD
и EDF можно сложить треугольник, приложив AB к CB, a ED и EF
к CD и AF. Стороны полученного треугольника равны сторонам
треугольника BDF. Следовательно, при симметрии относительно
прямых FB,BD и DF точки A,C и E переходят в центр O описанной
окружности треугольника BDF, а значит, AB||OF||DE.
-
6.54.
-
Предположим, что диагонали шестиугольника образуют
треугольник PQR. Обозначим вершины шестиугольника следующим
образом: вершина A лежит на луче QP, B — на RP, C —
на RQ и т. д. Так как прямые AD и BE делят площадь шестиугольника
пополам, то SAPEF + SPED = SPDCB + SABP
и SAPEF + SABP = SPDCB + SPED. Поэтому SABP = SPED, т. е.
|
AP · BP = EP · DP = (ER + RP)(DQ + QP) > ER · DQ. |
|
Аналогично CQ · DQ > AP · FR и FR · ER > BP · CQ.
Перемножая эти неравенства, получаем
AB · BP · CQ · DQ · FR · ER > ER · DQ · AP · FR · BP · CQ,
чего не может быть. Поэтому диагонали шестиугольника пересекаются в
одной точке.
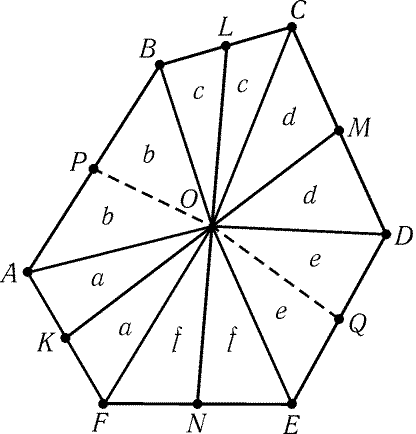
Рис. 6.12
6.55. Обозначим середины сторон выпуклого
шестиугольника ABCDEF так, как показано на рис. 6.12. Пусть O —
точка пересечения отрезков KM и LN. Площади треугольников, на
которые делят шестиугольник отрезки, соединяющие точку O с вершинами
и серединами сторон, обозначим так, как показано на том же рисунке.
Легко проверить, что SKONF = SLOMC, т. е. a + f = c + d.
Следовательно, ломаная POQ делит шестиугольник на две части равной
площади, а значит, отрезок PQ проходит через точку O.
6.56. а) Пусть O — центр описанной окружности. Так
как РAkOAk + 2 = 360° – 2РAkAk + 1Ak + 2 = j
- постоянная величина, то при повороте с центром O на угол j
точка Ak переходит в Ak + 2. Для нечетного n из этого следует,
что все стороны многоугольника A1… An равны.
б) Пусть a — длина стороны данного многоугольника. Если одна
из его сторон делится точкой касания с вписанной окружностью
на отрезки длиной x и a – x, то соседние с ней стороны тоже
делятся на отрезки длиной x и a – x (смежные отрезки соседних
сторон равны) и т. д. Для нечетного n из этого следует, что все
сторо-
|
ны многоугольника A1… An, делятся точками касания с
вписанной окружностью пополам, а значит, все его углы равны.
-
6.57.
-
Стороны многоугольника A1… An параллельны сторонам
правильного n-угольника. Отложим на лучах OA1,…,OAn равные
отрезки OB1,…,OBn. Тогда многоугольник B1… Bn
правильный и стороны многоугольника A1… An образуют равные углы
с его сторонами. Следовательно, OA1 : OA2 = OA2 : OA3 = … = OAn : OA1 = k, т. е. OA1 = kOA2 = k2OA3 = … = knOA1, а
значит, k = 1.
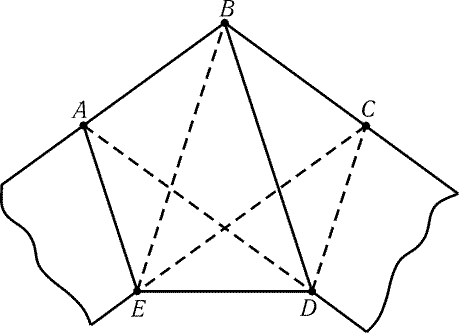 Рис. 6.13
6.58. Обозначим вершины пятиугольника так, как показано на
рис. 6.13. Если в треугольнике две высоты равны, то равны и стороны, на
которые опущены эти высоты. Рассматривая треугольники EAB, ABC
и BCD, получаем EA = AB, AB = BC и BC = CD. Поэтому трапеции EABC
и ABCD равнобедренные, т. е. РA = РB = РC.
Рассматривая треугольники ABD и BCE, получаем AD = BD и BE = CE.
Так как треугольники EAB, ABC, BCD равны, то BE = AC = BD.
Поэтому AD = BE и BD = CE, т. е. трапеции ABDE и CDEB
равнобедренные. Следовательно, ED = AB = BC = CD = AE и РE = РA = РB = РC = РD, т. е. ABCDE — правильный
пятиугольник.
6.59
Треугольник BMC равнобедренный с углом при вершине 30°
и углом при основании (180° – 30°)/2 = 75°.
Следовательно,
треугольники BAM и BCN равнобедренные с
углом 15° при основании. Поэтому
треугольник BMN правильный. Пусть O — центр квадрата,
P и Q
- середины отрезков MN и BK (рис. 6.14). Так как OQ —
средняя линия треугольника MBK, то OQ = BM/2 = MP = OP и РQON = РMBA = 15°,
а значит, РPOQ = РPON – РQON = 30°. Дальнейшее доказательство проводится аналогично.
|
6.60. Рассмотрим правильный
двенадцатиугольник A1… A12, вписанный в окружность
радиуса R. Ясно, что A1A7 = 2R, A1A3 = A1A11 = R.
Поэтому A1A7 = A1A3 + A1A11.
6.61. Для k = 3 решение задачи ясно из рис. 6.15. В самом деле,
A3A4 = OQ, KL = QP и MN = PA14, поэтому A3A4 + KL + MN = OQ + QP + PA14 = OA14 = R. Доказательство проводится аналогично и для
любого k.
6.62. Для доказательства достаточно применить результат
задач 5.86 и 5.77, б) к треугольнику AaAcAe и прямым AaAd,AcAf и AeAb. При решении задачи б) нужно еще
заметить, что sin 20°sin 70° = sin 20°sin 20° = (sin 40°)/2 = sin 30°sin 40°, а при решении
задачи в) нужно заметить, что sin 10°sin 80° = sin 30°sin 20°.
-
6.63.
-
Как и в предыдущей задаче, нужно проверить равенство
sin 2asin 2asin 8a
= sin asin 3asin 14a,
где a
= 180°/30 = 6°. Ясно, что sin 14a
= cos a,
поэтому 2sin asin 3asin 14a
= sin 2asin 3a. Остается
проверить, что sin 3a
= 2sin 2asin 8a
= cos 6a – cos 10a
= 1 – 2sin 23a – 1/2, т. е. 4sin 218° + 2sin 18° = 1 (см.
задачу 5.48).
-
6.64.
-
Пусть сначала n = 2m. Диагонали и стороны правильного
2m-угольника имеют m различных длин. Поэтому отмеченные точки
лежат на m – 1 концентрических окружностях (по n точек на каждой)
или в общем центре этих окружностей. Поскольку различные
окружности имеют не более двух общих точек, окружность, не
принадлежащая этому семейству концентрических окружностей,
содержит не более 1 + 2(m – 1) = 2m – 1 = n – 1 отмеченных точек.
Пусть теперь n = 2m + 1. Диагонали и стороны правильного
(2m + 1)-угольника имеют m различных длин. Поэтому отмеченные
точки лежат на m концентрических окружностях (по n точек на
каждой). Окружность, не принадлежащая этому семейству концентрических
окружностей, содержит не более 2m = n – 1 отмеченных точек.
В обоих случаях наибольшее число отмеченных точек, лежащих
на одной окружности, равно n.
-
6.65.
-
Обозначим центр многоугольника через O, вершины-
через A1,…,An. Предположим, что среди одноцветных
многоугольников нет равных, т. е. они имеют m = m1 < m2 < m3 < … < mk
сторон соответственно. Рассмотрим преобразование f, определенное на
множестве вершин n-угольника и переводящее вершину Ak в
вершину Amk : f(Ak) = Amk (считаем, что Ap + qn = Ap).
При этом преобразовании вершины правильного m-угольника переходят в
одну точку B, поэтому сумма векторов
, где Ai-
вершины m-угольника, равна
.
Поскольку РAmiOAmj = mРAiOAj вершины любого
правильного многоугольника с числом сторон больше m переходят при
рассматриваемом преобразовании в вершины правильного многоугольника.
Поэтому и сумма векторов
по всем вершинам
n-угольника и аналогичные суммы по вершинам m2-, m3-,
…, mk-угольников равны нулю. Получено противоречие с тем,
что сумма векторов
по вершинам m-угольника не
равна нулю. Поэтому среди одноцветных многоугольников найдутся два
равных.
-
6.66.
-
Пусть правильный (n – 1)-угольник B1… Bn – 1
вписан в правильный n-угольник A1… An. Можно считать,
что A1 и B1- наименее удаленные друг от друга вершины этих
многоугольников и точки B2,B3,B4 и B5 лежат на
сторонах A2A3, A3A4, A4A5 и A5A6. Пусть ai = РAi + 1BiBi + 1 и bi = РBiBi + 1Ai + 1,
где i = 1,2,3,4. По теореме синусов A2B2 :
B1B2 = sin a1 : sin j и B2A3 :
B2B3 = sin b2 : sin j, где j- угол при вершине
правильного n-угольника. Следовательно,
sin a1 + sin b2 = ansin j/an – 1 где an и an – 1-
стороны данных многоугольников. Аналогичные рассуждения показывают,
что sin a1 + sin b2 = sin a2 + sin b3 = sin a3 + sin b4.
Заметим теперь, что
sin ai + sin bi + 1 = 2sin ((ai + bi + 1)/2) cos ((ai – bi + 1)/2), и займемся вычислением ai + bi + 1
и ai – bi + 1. Так как ai + bi = 2p/n
и ai + 1 + bi = 2p/(n – 1), то ai + 1 = ai + 2p/(n(n – 1))
и bi + 1 = bi – 2p/(n(n – 1)), а значит,
| ai + bi + 1 = |
2p
n
|
– |
2p
n(n – 1)
|
|
- величина
постоянная и ai – bi + 1 = ai – 1 – bi + 4p/(n(n – 1)).
Следовательно, cos q
= cos (q + 2p/n(n – 1)) = cos (q + 4p/(n – 1)n)
для q
= (a1 – b2)/2. Получено противоречие, так как на интервале,
меньшем 2p, косинус не может принимать одно значение в трех
различных точках.
Замечание.
В правильный пятиугольник квадрат вписать можно (см. задачу 6.49).
-
6.67.
-
Пусть
. При
повороте вокруг точки O на угол 360°/n точка Ai
переходит в Ai + 1, а значит, вектор a переходит в себя,
т. е. a = 0.
Так как
и
,
то
|
®
XA
|
1
|
+ … + |
®
XA
|
n
|
= n |
®
XO
|
|
.
-
6.68.
-
Проведем через центр правильного
многоугольника A1… An прямую l, не проходящую через его
вершины. Пусть xi равно проекции вектора
на прямую,
перпендикулярную прямой l. Тогда все xi отличны от нуля и сумма
чисел xi, стоящих в вершинах правильного k-угольника, равна нулю,
поскольку равна нулю соответствующая сумма векторов
(см.
задачу 6.67).
-
6.69.
-
Согласно задаче 6.67
и
, где O — центр многоугольника X1…X10. Ясно, что если точка A расположена очень близко к вершине
многоугольника, а точка B — очень близко к середине стороны,
то AO > BO.
-
6.70.
-
Так как
|
AiX2 = | |
®
AiO
|
+ |
®
OX
|
|2 = AiO2 + OX2 + 2( |
®
AiO
|
, |
®
OX
|
) = R2 + d2 + 2( |
®
AiO
|
, |
®
OX
|
), |
|
то
|
е
| AiX2 = n(R2 + d2) + 2 |
ж
и
|
е
| |
®
AiO
|
, |
®
OX
|
ц
ш
|
= n(R2 + d2)
|
(см. задачу 6.67).
-
6.71.
-
Обозначим через Sk сумму квадратов расстояний от
вершины Ak до всех остальных вершин. Тогда
|
Sk = AkA12 + AkA22 + … + AkAn2 = |
|
|
= AkO2 + 2( |
®
AkO
|
, |
®
OA
|
1
|
) + A1O2 + … + AkO2 + 2( |
®
AkO
|
, |
®
OA
|
n
|
) + AnO2 = 2nR2, |
|
так как
.
Поэтому
. Поскольку квадрат каждой из
сторон и диагоналей дважды входит в эту сумму, искомая сумма
равна n2R2.
-
6.72.
-
Пусть Xk- образ точки X при повороте
относительно центра O данного n-угольника, переводящем Ak
в A1. При этом повороте отрезок AkX переходит в A1Xk.
Следовательно, A1X + … + AnX = A1X1 + … + A1Xn.
А так как n-угольник X1… Xn правильный,
то
|
®
A1X
|
1
|
+ … + |
®
A1X
|
n
|
= n |
®
A1O
|
|
(см. задачу 6.67),
а значит,
| A1X1 + … + AnXn і n |
®
A1O
|
|
.
-
6.73.
-
Пусть Bi- проекция точки X на прямую OAi.
Тогда
| (ei, x) = ( |
®
OA
|
i
|
, |
®
OB
|
i
|
+ |
®
BiX
|
) = ( |
®
OA
|
i
|
, |
®
OB
|
i
|
) = ±R · OBi
|
.
Точки B1,…,Bn лежат на окружности с диаметром OX и являются
вершинами правильного n-угольника при n нечетном и вершинами
n/2-угольника, взятыми по два раза, при n четном (см. задачу 2.9).
Поэтому
(см. задачу 6.70).
-
6.74.
-
Пусть e1,…,en- векторы, идущие
из центра данного n-угольника в его вершины; x -
единичный вектор, перпендикулярный прямой l. Искомая сумма
равна
(см. задачу 6.73).
-
6.75.
-
Пусть e1,…,en- единичные
векторы, направленные из центра O правильного n-угольника в
середины его сторон;
. Тогда расстояние от
точки X до i-й стороны равно |(x, ei) – r|. Поэтому
искомая сумма равна
|
е
| ((x, ei)2 – 2r(x, ei) + r2) = |
е
| (x, ei)2 + nr2
|
. Согласно задаче 6.73
.
-
6.76.
-
Пусть x- единичный вектор, параллельный
прямой l,
. Тогда квадрат длины проекции
стороны AiAi + 1 на прямую l равен (x, ei)2.
Согласно задаче 6.73
.
-
6.77.
-
Пусть
. Тогда
XAi4 = |a + ei|4 = (|a|2 + 2(a, ei) + |ei|2)2 = 4(R2 + (a,ei))2 = 4(R4 + 2R2(a,ei) + (a,ei)2).
Ясно, что
.
Согласно задаче 6.73
, поэтому
искомая сумма равна 4(nR4 + nR4/2) = 6nR4.
-
6.78.
-
а) Докажем сначала требуемое соотношение для u = e1. Пусть ei = (sin ji,cos ji),
причем cos j1 = 1. Тогда
е (e1,ei)ei = еcosji li = е( sinji cosji, cos2 ji ) = е( (sin2ji)/2, (1+cos2ji)/2 ) = (0,n/2) = ne1/2. Для u = e2 доказательство
проводится аналогично. Остается заметить, что любой вектор u можно
представить в виде u = le1 + me2.
б) Пусть B1… Bn- середины сторон данного многоугольника,
и
.
Тогда
|
®
XA
|
i
|
= |
®
OB
|
i
|
+ (u,ei)ei
|
. А так
как
, то
|
е
| |
®
XA
|
i
|
= |
е
| (u, ei)ei = nu/2 = n |
®
XO
|
/2
|
.
-
6.79.
-
Пусть e0,…,en – 1- векторы
сторон правильного n-угольника. Достаточно доказать, что,
переупорядочив эти векторы, можно получить такой набор векторов
{a1,…,an}, что
. Число n, не являющееся степенью простого числа, можно
представить в виде n = pq, где p и q — взаимно простые числа.
Докажем теперь, что набор {e0,ep,…, e(q – 1)p; eq,eq + p,…,eq + (q – 1)p,…,;e(p – 1)q + p,…,e(p – 1)q + (q – 1)p} искомый. Заметим
сначала, что если x1q + y1p є x2q + y2p mod pq,
то x1 є x2 mod p и y1 є y2 mod q, поэтому в
рассматриваемом наборе каждый из векторов e0,…,en – 1 встречается ровно один раз.
Концы векторов eq,eq + p,…,eq + (q – 1)p с
общим началом образуют правильный q-угольник, поэтому их сумма
равна нулю. Кроме того, векторы e0,ep,…,e(q – 1)p переходят в eq,eq + p,…,eq + (p – 1)q, при повороте на угол j
= 2p/p. Поэтому если
e0 + 2ep + … + qe(q – 1)p = b, то
(q + 1)eq + (q + 2)eq + n + … + 2qeq + (q – 1)p = q(eq + … + eq + (q – 1)p) + eq + 2eq + p + … + qeq + (q – 1)p = Rjb, где Rjb -
вектор, полученный из вектора b поворотом на
угол j
= 2p/p. Аналогичные рассуждения показывают, что для
рассматриваемого набора векторов
|
n
е
k = 1
|
kak = b + Rjb + … + R(p – 1)jb = 0
|
.
-
6.80.
-
Предположим, что на сторонах треугольника ABC внешним
образом построены квадраты ABB1A1, BCC2B2, ACC3A3 и
вершины A1, B1, B2, C2, C3, A3 лежат на одной окружности S.
Серединные перпендикуляры к отрезкам A1B1, B2C2, A3C3 проходят
через центр окружности S. Ясно, что серединные перпендикуляры к
отрезкам A1B1, B2C2, A3C3 совпадают с серединными
перпендикулярами к сторонам треугольника ABC, поэтому центр
окружности S совпадает с центром описанной окружности треугольника.
Обозначим центр описанной окружности треугольника ABC через O.
Расстояние от точки O до прямой B2C2 равно Rcos A + 2Rsin A,
где R — радиус описанной окружности треугольника ABC. Поэтому
OB22 = (Rsin A)2 + (Rcos A + 2Rsin A)2 = R2(3 + 2(sin 2A – cos 2A)) = R2(3 – 2Ц2cos (45° + 2A)).
Ясно, что для того, чтобы треугольник обладал требуемым свойством,
необходимо и достаточно, чтобы OB22 = OC32 = OA12, т. е.
cos (45° + 2РA) = cos (45° + 2РB) = cos (45° + 2РC). Это равенство выполняется при РA = РB = РC = 60°. Если же РA № РB, то
(45° + 2РA) + (45° + 2РB) = 360°,
т. е. РA + РB = 135°. Тогда РC = 45°
и РA = РC = 45°, РB = 90°
(или РB = 45°, РA = 90°). Мы видим, что
треугольник должен быть либо равносторонним, либо равнобедренным
прямоугольным.
-
6.81.
-
В любом треугольнике выполнено соотношение hc = ab/2R
(задача 12.33), поэтому pk = MAk · MAk + 1/2R. Следовательно,
|
p1p3… p2n – 1 = MA1 · MA2… MA2n/(2R)n = p2p4… p2n. |
|
-
6.82.
-
Пусть ABC — треугольник, вписанный в окружность S.
Обозначим расстояния от центра O окружности до сторон BC,CA
и AB через a,b и c соответственно. Тогда R + r = a + b + c, если
точка O лежит внутри треугольника ABC, и R + r = – a + b + c, если
точки O и A лежат по разные стороны от прямой BC (см.
задачу 12.38).
Каждая из диагоналей разбиения принадлежит двум треугольникам
разбиения. Для одного из этих треугольников точка O и оставшаяся
вершина лежат по одну сторону от диагонали, для другого - по разные
стороны. Разбиение n-угольника непересекающимися диагоналями на
треугольники состоит из n – 2 треугольников. Поэтому
сумма (n – 2)R + r1 + … + rn – 2 равна сумме расстояний от точки O до
сторон n-угольника (расстояния до сторон берутся с
соответствующими знаками). Из этого видно, что
сумма r1 + … + rn – 2 не зависит от разбиения.
-
6.83.
-
Пусть многоугольник A1… An вписан в окружность.
Рассмотрим точку A2ў, симметричную точке A2 относительно
серединного перпендикуляра к отрезку A1A3. Тогда
многоугольник A1A2ўA3… An
вписанный и его площадь равна
площади многоугольника A1… An. Таким образом можно поменять
местами любые две соседние стороны, а значит, можно поменять местами
любые две стороны. Поэтому к любой стороне можно «подогнать» любую
другую сторону, к ней- любую из оставшихся и т. д. Следовательно,
площадь n-угольника, вписанного в данную окружность, зависит только
от набора длин сторон, но не от их порядка.
-
6.84.
-
Без ограничения общности можно считать, что an-
наибольшее из чисел a1,…,an. Пусть n-угольник A1…An вписан в окружность с центром O. Тогда AiAi + 1 :
A1An = sin (РAiOAi + 1/2) : sin (РA1OAn/2).
Поэтому поступим следующим образом. Из
соотношения sin (ji/2) : sin (j/2) = ai : an
угол ji однозначно выражается через j, если ji < p. На
окружности радиуса 1 фиксируем точку An и рассмотрим такие переменные
точки A1,…,An – 1,Aўn, что ИAnA1 = j, И
A1A2 = j1,…,ИAn – 2An – 1 = jn – 2 и И
An – 1Anў = jn – 1, причем расположим эти точки двумя различными
способами, изображенными на рис. 6.16 (первый способ (рис. 6.16, а )
будет соответствовать n-угольнику, содержащему центр окружности,
а второй (рис. 6.16, б )- не содержащему). Остается доказать, что
при изменении j от 0 до p в одном из этих случаев
точка Anў совпадает с An (в самом деле, тогда с точностью до
подобия получается искомый n-угольник). Предположим, что в первом
случае при 0 Ј j Ј p точки Anў и An никогда не
совпадают, т. е. при j
= p выполняется
неравенство j1 + … + jn – 1 < p. Рисунок 6.16, б требует
некоторых комментариев: при малых углах sin a » a,
поэтому из условия задачи следует, что при малых углах точка An
действительно лежит на дуге A1Anў, так
как j1 + … + jn – 1 > j. Итак, при малых
углах j1 + … + jn – 1 > j, а если j
= p, то согласно
предположению j1 + … + jn – 1 < p = j. Поэтому в некоторый
момент j
= j1 + … + jn – 1, т. е. точки An и Anў
совпадают.
-
6.85.
-
Пусть h1,…,hn- расстояния от данной точки до
соответствующих сторон, a1,…,an- расстояния от вершин
многоугольника до точек касания. Тогда произведение площадей как
красных, так и синих треугольников
равно a1… anh1… hn/2n.
-
6.86.
-
Пусть OHi- высота треугольника OAiAi + 1.
Тогда РHi – 1OAi = РHiOAi = ji !-- -->. Из условия задачи
следует, что j1 + j2 = jn + 1 + jn + 2,jn + 2 + jn + 3 = j2 + j3,j3 + j4 = jn + 3 + jn + 4,…,jn – 2 + jn–1 = j2n – 2 + j2n – 1
(при записи последнего равенства мы учли, что n нечетно)
и jn – 1 + 2jn + jn + 1 = j2n – 1 + 2j2n + j1. Складывая все эти равенства,
получаем jn – 1 + jn = j2n – 1 + j2n, что и требовалось.
-
6.87.
-
Пусть O — центр данной окружности.
Тогда
, а значит,
| XAi2 = XO2 + OAi2 + 2( |
®
XO
|
, |
®
OA
|
i
|
) = d2 + r2 + 2( |
®
XO
|
, |
®
OA
|
i
|
)
|
. Так
как
| a1 |
®
OA
|
1
|
+ … + an |
®
OA
|
n
|
= |
®
0
|
|
(см. задачу 13.4),
то a1XA12 + … + anXAn2 = (a1 + … + an)(d2 + r2).
-
6.88.
-
Согласно задаче 5.8 bi – 1bi/ai2 = sin 2(Ai/2).
Для решения задачи а) достаточно перемножить все такие равенства, а для
решения задачи б) произведение равенств с четным индексом i нужно
поделить на произведение равенств с нечетным индексом i.
-
6.89.
-
Пусть BC — синяя сторона, AB и CD —
соседние с BC стороны. По условию стороны AB и CD красные.
Предположим, что многоугольник описанный; P,Q,R — точки касания
сторон AB,BC,CD с вписанной окружностью. Ясно, что BP = BQ, CR = CQ и
отрезки BP, CR граничат только с одним синим отрезком. Поэтому сумма
длин красных сторон не меньше суммы длин синих сторон. Получено
противоречие с тем, что сумма длин красных сторон меньше половины
периметра. Поэтому в многоугольник нельзя вписать окружность.
-
6.90.
-
Пусть выпуклый n-угольник имеет k острых углов.
Тогда сумма его углов меньше k · 90° + (n – k) · 180°. С другой стороны, сумма углов n-угольника
равна (n – 2) · 180°. Поэтому (n – 2) · 180° < k · 90° + (n – k) · 180°,
т. е. k < 4. Поскольку k — целое число, k Ј 3.
Для любого n і 3 существует выпуклый n-угольник с тремя
острыми углами (рис. 6.17).
-
6.91.
-
Предположим, что несмежные стороны AB и CD равны
по длине наибольшей диагонали. Тогда AB + CD і AC + BD. Но
согласно задаче 9.14 AB + CD < AC + BD. Получено противоречие,
поэтому стороны, равные по длине наибольшей диагонали, должны
быть смежными, т. е. таких сторон не больше двух.
Пример многоугольника с двумя сторонами, равными по длине
наибольшей диагонали, приведен на рис. 6.18. Ясно, что такой
n-угольник существует при любом n > 3.
-
6.92.
-
Докажем, что n Ј 5. Пусть AB = 1, а C —
вершина, не соседняя ни с A, ни с B. Тогда |AC – BC| < AB = 1.
Поэтому AC = BC, т. е. точка C лежит на серединном перпендикуляре к
стороне AB. Таким образом, кроме вершин A,B,C многоугольник может
иметь еще лишь две вершины.
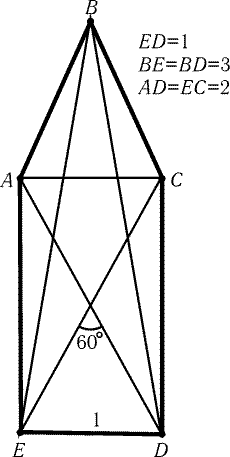
Рис. 6.19
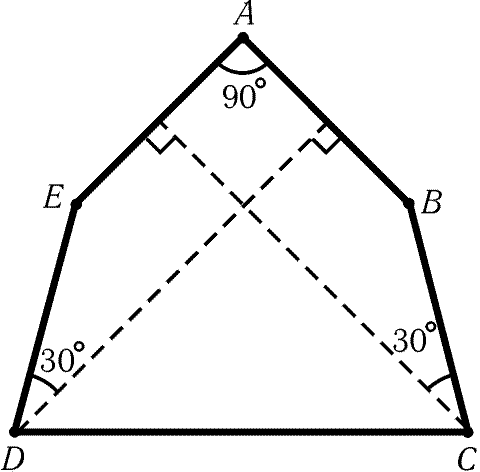
Рис. 6.20
Пример пятиугольника, обладающего требуемым свойством, приведен на
рис. 6.19. Поясним, как он устроен. ACDE — прямоугольник, AC = ED = 1
и РCAD = 60°. Точка B задается условием BE = BD = 3.
Примером четырехугольника, обладающего требуемым свойством,
является прямоугольник ACDE на том же рисунке.
6.93. Пример пятиугольника, удовлетворяющего условию задачи,
приведен на рис. 6.20. Поясним, как он устроен. Возьмем
равнобедренный прямоугольный треугольник EAB, проведем серединные
перпендикуляры к сторонам EA,AB и на них построим точки C
и D так, что ED = BC = AB (т. е. прямые BC и ED образуют
с соответствующими серединными перпендикулярами углы в 30°).
Ясно, что DE = BC = AB = EA < EB < DC и DB = DA = CA = CE > EB.
Докажем теперь, что пятая сторона и пятая диагональ не могут
иметь общей точки. Предположим, что пятая сторона AB имеет
общую точку A с пятой диагональю. Тогда пятая диагональ- это AC
или AD. Разберем эти два случая.
В первом случае DAED = DCDE, поэтому при симметрии
относительно серединного перпендикуляра к отрезку ED точка A
переходит в точку C. Точка B при этой симметрии остается на
месте, так как BE = BD. Поэтому отрезок AB переходит в CB,
т. е. AB = CB. Получено противоречие.
Во втором случае DACE = DEBD, поэтому при симметрии
относительно биссектрисы угла AED отрезок AB переходит в DC,
т. е. AB = CD. Получено противоречие.
6.94. Рассмотрим две соседние вершины A1 и A2.
Если РA1OA2 і 90°,
то OA1 = OA2, так как к основанию равнобедренного треугольника не может прилегать прямой или
тупой угол.
Пусть теперь РA1OA2 < 90°. Проведем через точку O
прямые l1 и l2, перпендикулярные прямым OA1 и OA2.
Обозначим области, на которые эти прямые разбивают плоскость, так,
как показано на рис. 6.21. Если в области (3) есть вершина Ak,
то A1O = AkO = A2O, поскольку РA1OAk і 90°
и РA2OAk і 90°. Если же в области (3) нет вершин
многоугольника, то в области (1) есть вершина Ap и в области (2)
есть вершина Aq. (Если бы в одной из областей (1), (2) не
было вершин многоугольника, то точка O оказалась бы вне многоугольника.)
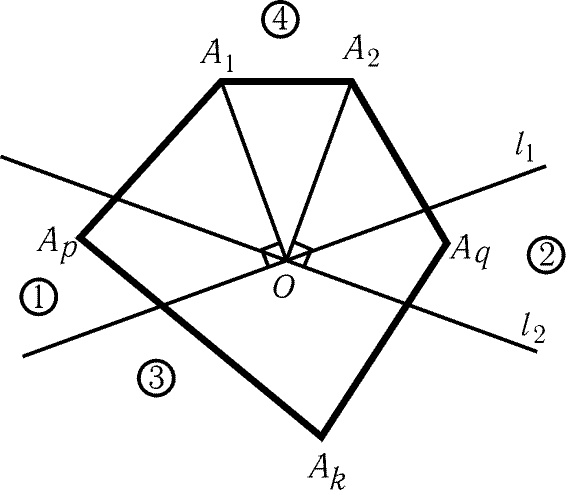
Рис. 6.21
Так как РA1OAq і 90°, РA2OAp і 90°
и РApOAq і 90°, то A1O = AqO = ApO = A2O.
Остается заметить, что если расстояния от точки O до любой
пары соседних вершин многоугольника равны, то равны и все
расстояния от точки O до вершин многоугольника.
6.95.
Пусть прямые AB и DE пересекаются в точке G, BC и EF в точке H,
CD и FA в точке K. Пусть, далее, X и Y - точки пересечения
описанной окружности треугольника EBH с прямыми AB и DE. Покажем, что
соответственные стороны треугольников ADK и XYH параллельны. (Из этого
следует, что прямая KH проходит через точку G.)
Из равенств
Р(YX,AB) = Р(YX,XB) = Р(YE,EB) = Р(DE,EB) = Р(DA,AB)
следует, что AD|| XY. После этого из равенств
Р(XY,YH) = Р(XB,BH) = Р(AB,BC) = Р(AD,DC) = Р(AD,DK)
следует, что DK|| YH, а из равенств
Р(YH,XH) = Р(YE,EH) = Р(DE,EF) = Р(DA,AF) = Р(DA,AK)
следует, что AK|| XH.
Отметим, что мы нигде не пользовались тем, что шестиугольник ABCDEF выпуклый;
вместо шестиугольника можно взять самопересекающуюся шестизвенную ломаную с
вершинами на окружности.
6.96. Пусть A2,B2 и C2- указанные точки пересечения
прямых. Применяя теорему Паскаля к точкам M,A1,A,C,B,B1,
получаем, что точки A2,B2 и R лежат на одной прямой. Аналогично
точки A2,C2 и R лежат на одной прямой. Следовательно,
точки A2,B2,C2 и R лежат на одной прямой.
-
6.97.
-
Поскольку углы APT, ART, AST и AQT прямые, то
точки A, P, R, T, S, Q лежат на окружности, построенной
на отрезке AT как на диаметре. Следовательно, по теореме Паскаля
(задача 30.50) точки B, C и X лежат на одной прямой.
-
6.98.
-
Точки A1 и B1 лежат на окружности S с
диаметром AB. Пусть A4 и B4- точки пересечения
прямых AA2 и BB2 с прямой A3B3. Согласно задаче 2.42, а) эти
точки лежат на окружности S. Прямые A1B и A4A пересекаются в
точке A2, а прямые BB4 и AB1- в точке B2. Поэтому,
применяя теорему Паскаля к точкам B1,A1,B,B4,A4,A, получаем, что
точка пересечения прямых B1A1 и B4A4 (последняя прямая
совпадает с A3B3) лежит на прямой A2B2.
-
6.99.
-
Пусть K — точка пересечения прямых BC и MN.
Применяя теорему Паскаля к точкам A,M,N,D,C,B, получаем, что
точки E,K и F лежат на одной прямой, а значит, K — точка
пересечения прямых MN и EF.
-
6.100.
-
Пусть точки B1 и C1 симметричны точкам B и C
относительно точки O. Тогда точка X лежит на прямых AB1 и
C1D. Применим теорему Паскаля к шестиугольнику AB1BDC1C.
Прямые AB1 и DC1 пересекаются в точке X, прямые BB1 и
CC1 - в точке O; прямые BD и AC - диагонали
четырехугольника.
-
6.101.
-
Пусть лучи PA и QA пересекают окружность в
точках P2 и Q2, т. е. P1P2 и Q1Q2 - диаметры данной
окружности. Применим теорему Паскаля к
шестиугольнику PP2P1QQ2Q1. Прямые PP2 и QQ2 пересекаются в
точке A, а прямые P1P2 и Q1Q2 пересекаются в точке O,
поэтому точка пересечения прямых P1Q и Q1P лежит на прямой AO.
-
6.102.
-
Пусть B1 и C1 - середины дуг AC и AB (имеются в виду
дуги, не содержащие точек B и C соответственно). Согласно
задаче 3.42, а) точки M и N лежат на отрезках KC1 и
KB1.
Применим теорему Паскаля к шестиугольнику C1CABB1K. Прямые
CC1 и BB1 - биссектрисы; прямые CA и B1K
пересекаются в точке N, прямые AB и C1K - в точке M.
Отметим, что задача 3.46 является частным случаем этой задачи.
-
6.103.
-
Пусть данные точки A,B,C,D,E лежат на одной
окружности. Предположим, что мы построили точку F той же
окружности. Обозначим через K,L,M точки пересечения прямых AB
и DE, BC и EF, CD и FA соответственно. Тогда по теореме
Паскаля точки K,L,M лежат на одной прямой.
Из этого вытекает следующее построение. Проведем через точку E
произвольную прямую a и обозначим точку ее пересечения с прямой BC
через L. Затем построим точку K пересечения прямых AB и DE
и точку M пересечения прямых KL и CD. Наконец, F — точка
пересечения прямых AM и a. Докажем, что F лежит на нашей
окружности. Пусть F1- точка пересечения окружности и прямой a.
Из теоремы Паскаля следует, что F1 лежит на прямой AM, т. е. F1
является точкой пересечения a и AM. Поэтому F1 = F.
-
6.104.
-
Пусть P и Q — точки пересечения прямой A3A4
с A1A2 и A1A6, а R и S — точки пересечения
прямой A4A5 с A1A6 и A1A2. Тогда
A2K : A3L = A2P : A3P,A3L : A6M = A3Q : A6Q
и A6M : A5N = A6R : A5R. Поэтому требуемое
соотношение A2K : A5N = A2 S : A5 S перепишется в виде
|
|
A2P
A3P
|
· |
A3Q
A6Q
|
· |
A6R
A5R
|
· |
A5S
A2S
|
= 1. |
|
Пусть T — точка пересечения прямых A2A3 и A5A6; по теореме
Паскаля точки S,Q и T лежат на одной прямой. Применяя теорему
Менелая (см. задачу 5.64) к треугольнику PQS и точкам T,A2
и A3, а также к треугольнику RQS и точкам T,A5 и A6, получаем
|
|
A2P
A2S
|
· |
A3Q
A3P
|
· |
TS
TQ
|
= 1 и
|
TQ
TS
|
· |
A5S
A5R
|
· |
A6R
A6Q
|
= 1. |
|
Перемножая эти равенства, получаем требуемое. (Отношения отрезков
следует считать ориентированными.)

 Глава 6. Задачи для самостоятельного решения |
Глава 6. Задачи для самостоятельного решения | 

 Глава 6. Задачи для самостоятельного решения |
Глава 6. Задачи для самостоятельного решения | 







