| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
7.1.
-
Пусть O1 и O2- центры колес радиусов r1
и r2 соответственно. Если M — точка пересечения внутренних
касательных, то O1M : O2M = r1 : r2. Из этого условия
легко получить, что расстояние от точки M до прямой l
равно 2r1r2/(r1 + r2). Поэтому все точки пересечения общих
внутренних касательных лежат на прямой, параллельной прямой l и
отстоящей от нее на расстояние 2r1r2/(r1 + r2).
-
7.2.
-
Пусть O — точка пересечения прямых AB и CD.
Отложим на лучах OA и OD отрезки OK и OL, равные AB и CD
соответственно. Тогда SABX + SCDX = SKOX + SLOX±SKXL.
Следовательно, площадь треугольника KXL постоянна, т. е. точка X
лежит на прямой, параллельной KL.
-
7.3.
-
Пусть a и b- единичные векторы,
параллельные данным прямым;
. Сумма длин проекций
вектора x на данные прямые
равна |(a,x)| ± |(b,x)| = |(a + b,x)|, причем смена знака
происходит на перпендикулярах, восставленных из точки O к данным
прямым. Поэтому искомое ГМТ- прямоугольник, стороны которого
параллельны биссектрисам углов между данными прямыми, а вершины лежат
на указанных перпендикулярах.
-
7.4.
-
Пусть l — прямая, проходящая через середины
сторон BC и AD. Предположим, что точка X не лежит на прямой l,
например что точки A и X лежат по одну сторону от прямой l.
Тогда AX < DX и BX < CX, а значит, AX + BX < CX + DX. Поэтому прямая l
- искомое ГМТ.
-
7.5.
-
Пусть N — такая точка, что
.
Тогда РNAM = РDMA и РNBM = РBMC, поэтому
четырехугольник AMBN вписанный. Диагонали вписанного
четырехугольника AMBN равны, поэтому AM||BN или BM||AN. В
первом случае РAMD = РMAN = РAMB, а во втором
случае РBMC = РMBN = РBMA.
Если РAMB = РAMD, то РAMB + РBMC = 180°
и точка M лежит на диагонали AC, а если РBMA = РBMC, то
точка M лежит на диагонали BD. Ясно также, что если точка M
лежит на одной из диагоналей, то РAMD + РBMC = 180°.
-
7.6.
-
Введем систему координат, выбрав точку A в качестве
начала координат и направив ось Ox по лучу AB. Пусть точка M
имеет координаты (x,y). Тогда AM2 = x2 + y2 и BM2 = (x – a)2 + y2,
где a = AB. Поэтому AM2 – BM2 = 2ax – a2. Эта величина равна k для
точек M с координатами ((a2 + k)/2a,y); все такие точки лежат на
прямой, перпендикулярной AB.
-
7.7.
-
Пусть A и B — точки пересечения окружностей S
и S1. Тогда XM2 = XA · XB = XO2 – R2, где O и R — центр и
радиус окружности S. Поэтому XO2 – XM2 = R2, а значит, точки X
лежат на перпендикуляре к прямой OM (см. задачу 7.6).
-
7.8.
-
Пусть O1 и O2- центры данных окружностей,
R1 и R2- их радиусы. Окружность радиуса r с центром X
пересекает первую окружность в диаметрально противоположных точках
тогда и только тогда, когда r2 = XO12 + R12, поэтому искомое ГМТ
состоит из таких точек X, что XO12 + R12 = XO22 + R22, все такие
точки X лежат на прямой, перпендикулярной O1O2 (задача 7.6).
-
7.9.
-
Пусть O — центр окружности, R — ее радиус,
M — точка пересечения касательных, проведенных через концы
хорды, содержащей точку A, P — середина этой хорды.
Тогда OP · OM = R2 и OP = OA cos j, где j
= РAOP.
Поэтому AM2 = OM2 + OA2 – 2OM · OAcos j
= OM2 + OA2 – 2R2, а значит,
величина OM2 – AM2 = 2R2 – OA2 постоянна. Следовательно, все точки M
лежат на прямой, перпендикулярной OA (см. задачу 7.6).
-
7.10.
-
Пусть P и Q — середины диагоналей AC и BD.
Тогда AX2 + CX2 = 2PX2 + AC2/2 и BX2 + DX2 = 2QX2 + BD2/2 (см.
задачу 12.11, а)), поэтому в задаче б) искомое ГМТ состоит из таких
точек X, что PX2 – QX2 = (BD2 – AC2)/4, а в задаче a) P = Q, поэтому
рассматриваемая величина равна (BD2 – AC2)/2.
-
7.11.
-
Пусть M и N — концы данного отрезка, O —
его середина. Точка B лежит на окружности с диаметром MN,
поэтому OB = MN/2. Траекторией точки O является часть окружности
радиуса MN/2 с центром B, заключенная внутри угла ABC.
-
7.12.
-
Пусть M — данная точка, O — центр данной
окружности. Если X — середина хорды AB, то XO^AB.
Следовательно, искомое ГМТ является окружностью с диаметром MO.
-
7.13.
-
Проведем через точку M общую касательную к окружностям.
Пусть O — точка пересечения этой касательной с прямой AB.
Тогда AO = MO = BO, т. е. O — середина отрезка AB. Точка M лежит
на окружности с центром O и радиусом AB/2. Множеством точек M
является окружность с диаметром AB (точки A и B следует
исключить).
-
7.14.
-
При k = 1 получаем серединный перпендикуляр к
отрезку AB. В дальнейшем будем считать, что k № 1 .
Введем систему координат на плоскости так, чтобы точки A
и B имели координаты ( – a,0) и (a,0) соответственно. Если
точка M имеет координаты (x,y), то
|
AM2
BM2
|
= |
(x + a)2 + y2
(x – a)2 + y2
|
|
. Уравнение
приводится к виду
|
|
ж
и
|
x + |
1 + k2
1 – k2
|
a |
ц
ш
|
2
|
+ y2 = |
ж
и
|
|
2ka
1 – k2
|
|
ц
ш
|
2
|
. |
|
Это уравнение является уравнением окружности с
центром
|
ж
и
|
– |
1 + k2
1 – k2
|
a,0 |
ц
ш
|
|
и
радиусом
.
-
7.15.
-
Пусть прямая AB пересекает окружность S в точках E
и F, причем точка E лежит на отрезке AB. Тогда PE —
биссектриса треугольника APB, поэтому РEPB = РEPA = РEFP. А так как РEPF = 90°, то PB^EF.
-
7.16.
-
а) Рассматриваемые окружности являются окружностями
Аполлония для пар вершин треугольника ABC, поэтому если X —
общая точка окружностей Sa и Sb, то XB : XC = AB : AC
и XC : XA = BC : BA, т. е. XB : XA = CB : CA, а
значит, точка X принадлежит окружности Sc. Ясно также, что
если AB > BC, то точка D лежит внутри окружности Sb, а
точка A — вне ее. Следовательно, окружности Sa и Sb
пересекаются в двух различных точках.
Для завершения доказательства остается воспользоваться результатом
задачи 7.49.
б) Согласно задаче а) MA = l/a, MB = l/b и MC = l/c. Пусть B1
и C1- проекции точки M на прямые AC и AB. Точки B1
и C1 лежат на окружности с диаметром MA, поэтому B1C1 = MAsin B1AC1 = (l/a)(a/2R) = l/2R, где R — радиус описанной окружности
треугольника ABC. Аналогично A1C1 = A1B1 = l/(2R).
-
7.17.
-
Пусть O1 и O2- такие точки,
что
и
. Легко
проверить, что если BM > 2AM, то точка M лежит внутри окружности S1
радиуса 2AB/3 с центром O1 (см. задачу 7.14), а если CM > 2BM, то
точка M лежит внутри окружности S2 радиуса 2AB/3 с
центром O2. Так как O1O2 > BO1 = 4AB/3, а сумма радиусов
окружностей S1 и S2 равна 4AB/3, то эти окружности не
пересекаются. Следовательно, если BM = qAM и CM = qBM, то q < 2.
-
7.18.
-
а) Пусть O — точка пересечения высот AA1
и BB1. Точки A1 и B1 лежат на окружности с диаметром CO.
Следовательно, РAOB = 180° – РC. Поэтому искомое
ГМТ- окружность, симметричная данной относительно прямой AB
(точки, проецирующиеся в точки A и B, следует исключить).
б) Если O — точка пересечения биссектрис треугольника ABC,
то РAOB = 90° + РC/2. На каждой из двух дуг AB
угол C постоянен, поэтому искомым ГМТ являются две дуги, из которых
отрезок AB виден под углом 90° + РC/2 (точки A и B
следует исключить).
-
7.19.
-
Точки P и Q лежат на окружности с диаметром DX,
поэтому Р(QD,DX) = Р(QP,PX) = Р(AP,BP) = 45°,
т. е. точка X
лежит на прямой CD.
-
7.20.
-
а) Если точка A1 пройдет по окружности дугу
величиной 2j, то точка B1 тоже пройдет дугу величиной 2j,
а значит, прямые AA1 и BB1 повернутся на угол j и угол между
ними не изменится.
Поэтому точка M перемещается по окружности, содержащей точки A
и B.
б) Пусть прямые AA1,BB1 и CC1 в некоторый момент пересекаются в
точке P. Тогда, например, точка пересечения прямых AA1 и BB1
перемещается по описанной окружности треугольника ABP. Ясно также,
что описанные окружности треугольников ABP,BCP и CAP имеют
единственную общую точку P.
-
7.21.
-
Предположим, что точки A и C лежат на противоположных
сторонах прямоугольника. Пусть M и N — середины отрезков AC
и BD соответственно. Проведем через точку M прямую l1,
параллельную сторонам прямоугольника, на которых лежат точки A и C,
а через точку N прямую l2, параллельную сторонам прямоугольника,
на которых лежат точки B и D. Пусть O — точка пересечения
прямых l1 и l2. Ясно, что точка O лежит на окружности S,
построенной на отрезке MN как на диаметре. С другой стороны,
точка O является центром прямоугольника. Ясно, что прямоугольник
можно построить для любой точки O, лежащей на окружности S.
Остается заметить, что на противоположных сторонах прямоугольника
могут лежать также точки A и B, A и D. Поэтому
искомым ГМТ является объединение трех окружностей.
-
7.22.
-
Легко проверить, что точки высот треугольника ABC
обладают требуемым свойством. Предположим, что требуемым
свойством обладает точка X, не лежащая ни на одной из высот
треугольника ABC. Тогда прямая BX пересекает высоты AA1 и CC1
в точках X1 и X2. Так как РXAB + РXBC + РXCA = 90° = РX1AB + РX1BC + РX1CA, то РXAB – РX1AB = РX1CA – РXCA,
т. е. Р(XA,AX1) = Р(X1C,CX). Следовательно, точка X
лежит на описанной окружности треугольника AXCў, где точка Cў
симметрична C относительно прямой BX. Аналогично доказывается, что
точка X2 лежит на этой окружности, а значит, прямая BX пересекает
эту окружность в трех различных точках. Получено противоречие.
-
7.23.
-
Пусть K — точка касания прямой MX и данной
полуокружности, а P — проекция точки M на диаметр. В
прямоугольных треугольниках MPX и OKX равны гипотенузы и РPXM = РOXK, а значит, эти треугольники равны и, в частности,
MP = KO = R, где R — радиус данной полуокружности. Следовательно,
точка M лежит на прямой l, параллельной диаметру полуокружности и
касающейся полуокружности. Пусть AB — отрезок прямой l,
проекцией которого является диаметр полуокружности. Из точки
прямой l, лежащей вне отрезка AB, нельзя провести касательную к
данной полуокружности, так как касательная, проведенная к окружности,
будет касаться другой полуокружности. Искомым ГМТ является
отрезок AB, из которого выброшены точки A и B и его середина.
-
7.24.
-
Пусть H — основание высоты hb треугольника ABC
и hb = b. Обозначим через Bў точку пересечения перпендикуляра к
прямой AB, проведенного через точку A, и перпендикуляра к
прямой AH, проведенного через точку C. Прямоугольные
треугольники ABўC и BAH равны, так как РABўC = РBAH
и AC = BH. Поэтому ABў = AB, т. е. точка C лежит на окружности с
диаметром ABў.
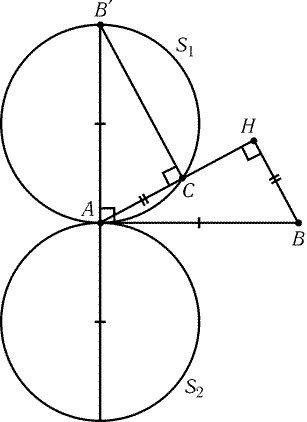
Рис. 7.1
Пусть S1 и S2- образы окружности S с диаметром AB при
поворотах на ±90° с центром A (рис. 7.1). Мы доказали, что
точка C № A принадлежит объединению окружностей S1 и S2.
Обратно, пусть точка C № A принадлежит окружности S1 или S2,
ABў- диаметр соответствующей окружности. Тогда РABўC = РHAB и AўB = AB, поэтому AC = HB.
7.25. Пусть O — центр окружности, N — точка
пересечения прямых OM и QP. Опустим из точки M перпендикуляр MS
на прямую OP. Из подобия треугольников ONQ и OQM, OPN и OMS
получаем ON : OQ = OQ : OM и OP : ON = OM : OS.
Перемножая эти равенства, получаем OP : OQ = OQ : OS.
Поэтому OS = OQ2 : OP является постоянной величиной. А так как
точка S лежит на прямой OP, ее положение не зависит от выбора
точки Q. Искомым ГМТ является прямая, перпендикулярная прямой OP и
проходящая через точку S.
-
7.26.
-
Пусть O — середина отрезка AB, M — точка
пересечения медиан треугольника ABC. При гомотетии с центром O и
коэффициентом 1/3 точка C переходит в точку M. Поэтому точки
пересечения медиан треугольников ABC лежат на окружности S,
являющейся образом исходной окружности при гомотетии с центром O
и коэффициентом 1/3. Для получения искомого ГМТ из окружности S
нужно выбросить образы точек A и B.
-
7.27.
-
Пусть O — середина высоты BH, M — середина
отрезка AC, D и E — середины сторон RQ и PS
соответственно (рис. 7.2).
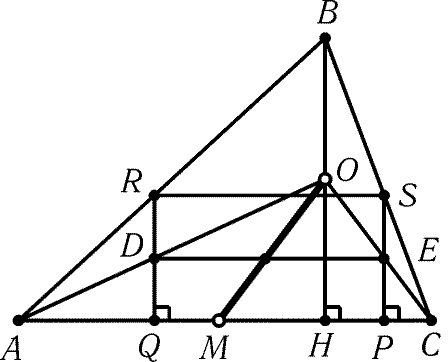
Рис. 7.2
Точки D и E лежат на прямых AO и CO соответственно. Середина
отрезка DE является центром прямоугольника PQRS. Ясно, что она
лежит на отрезке OM. Искомым ГМТ является отрезок OM, за
исключением его концов.
7.28. Пусть O1 и O2- центры данных окружностей
(точка P лежит на окружности с центром O1), O — середина
отрезка O1O2; Pў,Qў и Oў- проекции точек O1,O2 и O
на прямую PQ. При вращении прямой PQ точка Oў пробегает
окружность S с диаметром AO. Ясно, что при гомотетии с центром A
и коэффициентом 2 отрезок PўQў переходит в отрезок PQ, т. е.
точка Oў переходит в середину отрезка PQ. Поэтому искомым ГМТ
является образ окружности S при этой гомотетии.
7.29. Пусть P и Q — центры описанных окружностей
треугольников AMB и CMB. Точка M принадлежит искомому ГМТ,
если BPMQ — ромб, т. е. точка M является образом середины
отрезка PQ при гомотетии с центром B и коэффициентом 2. А так как
проекции точек P и Q на прямую AC являются серединами
отрезков AB и BC, середины всех отрезков PQ лежат на одной
прямой. (Точку прямой AC из полученного ГМТ следует исключить.)
-
7.30.
-
Точка P проходит через точку O в момент t1,
точка Q — в момент t2. В момент (t1 + t2)/2 точки P и Q
находятся от точки O на одинаковом расстоянии, равном |t1 – t2|v/2.
Проведем в этот момент перпендикуляры к прямым в точках P и Q.
Легко проверить, что точка пересечения этих перпендикуляров является
искомой.
-
7.31.
-
Обозначим середины диагоналей AC и BD
четырехугольника ABCD через M и N соответственно. Ясно,
что SAMB = SBMC и SAMD = SDMC,
т. е. SDABM = SBCDM.
Поскольку при перемещении точки M параллельно BD площади
четырехугольников DABM и BCDM не изменяются,
то SDABO = SBCDO. Аналогичные рассуждения для точки N
показывают, что SABCO = SCDAO.
Поэтому SADO + SABO = SBCO + SCDO
и SABO + SBCO = SCDO + SADO,
а значит, SADO = SBCO = S1
и SABO = SCDO = S2, т. е.
площадь каждой из четырех частей, на
которые отрезки, соединяющие точку O с серединами сторон
четырехугольника, разбивают его, равна (S1 + S2)/2.
-
7.32.
-
Опустим из точки B высоту BB1. Тогда AD = B1D
и CE = B1E. Ясно, что если MD < AD, то точка M лежит на
отрезке AB1, т. е. вне отрезка B1C. Следовательно, ME > EC.
-
7.33.
-
Предположим, что все вершины многоугольника удалены
от точки Q не меньше, чем точки от P. Тогда все вершины
многоугольника лежат в той же полуплоскости, заданной серединным
перпендикуляром к отрезку PQ, что и точка P, а точка Q лежит
в другой полуплоскости. Следовательно, точка Q лежит вне
многоугольника, что противоречит условию.
-
7.34.
-
Найдем ГМТ M, для которых MA > MB и MA > MC.
Проведем серединные перпендикуляры l1 и l2 к отрезкам AB и AC.
MA > MB для точек, лежащих внутри полуплоскости, заданной
прямой l1 и не содержащей точку A. Поэтому искомым ГМТ
является пересечение полуплоскостей (без границ), заданных
прямыми l1,l2 и не содержащих точку A. Если точки A,B,C не
лежат на одной прямой, то это ГМТ всегда непусто. Если A,B,C лежат на
одной прямой, но A не лежит на отрезке BC, то это ГМТ тоже непусто.
Если же A лежит на отрезке BC, то это ГМТ пусто, т. е. для любой
точки M либо MA Ј MB, либо MA Ј MC.
-
7.35.
-
Пусть O — середина диагонали AC. Проекции
точек B и D на прямую AC лежат на отрезке AO, поэтому проекция
точки M тоже лежит на отрезке AO.
-
7.36.
-
Проведем серединный перпендикуляр l к отрезку AO.
Ясно, что AM і OM тогда и только тогда, когда точка M лежит по ту
же сторону от прямой l, что и точка O (или лежит на прямой l).
Поэтому искомым ГМТ является ромб, образованный серединными
перпендикулярами к отрезкам OA, OB, OC и OD.
-
7.37.
-
Искомое ГМТ заштриховано на рис. 7.3 (граница входит
в ГМТ).
-
7.38.
-
Пусть A1 и B1- середины сторон CB и AC
соответственно. Искомым ГМТ является внутренность
четырехугольника OA1CB1.
-
7.39.
-
Проведем общие касательные к данным кругам (рис. 7.4).
Легко проверить, что точки, принадлежащие заштрихованным областям
(но не их границам), удовлетворяют требуемому условию, а точки,
не лежащие в этих областях, не удовлетворяют этому условию.
-
7.40.
-
Пусть перпендикуляры, опущенные из точек A1,B1,C1 на
прямые BC,CA,AB, пересекаются в точке M. Так как точки B1
и M лежат на одном перпендикуляре к прямой AC,
то B1A2 – B1C2 = MA2 – MC2. Аналогично C1B2 – C1A2 = MB2 – MA2
и A1C2 – A1B2 = MC2 – MB2. Складывая эти равенства, получаем
A1B2 + C1A2 + B1C2 = B1A2 + A1C2 + C1B2.
Обратно, пусть A1B2 + C1A2 + B1C2 = B1A2 + A1C2 + C1B2.
Обозначим точку пересечения перпендикуляров, опущенных из точек A1
и B1 на прямые BC и AC, через M. Проведем через точку M
прямую l, перпендикулярную прямой AB. Если C1ў- точка на
прямой l, то, согласно предыдущему,
A1B2 + C1ўA2 + B1C2 = B1A2 + A1C2 + C1ўB2.
Поэтому C1ўA2 – C1ўB2 = C1A2 – C1B2. Согласно задаче 7.6 ГМТ X,
для которых XA2 – XB2 = k, является прямой, перпендикулярной
отрезку AB. Поэтому перпендикуляр, опущенный из точки C1 на
прямую AB, проходит через точку M, что и требовалось.
-
7.41.
-
Положим A1 = A, B1 = B и C1 = C. Из очевидного равенства
AB2 + CA2 + BC2 = BA2 + AC2 + CB2 получаем, что высоты, опущенные
из точек A,B и C на стороны BC, CA и AB, пересекаются в одной
точке.
-
7.42.
-
Достаточно воспользоваться результатом задачи 7.40.
-
7.43.
-
а) Эта задача является очевидным следствием задачи 7.40.
б) Пусть при повороте на 90° относительно некоторой точки
треугольник A1B1C1 переходит в A2B2C2. Перпендикуляры к
сторонам треугольника A2B2C2 параллельны соответствующим
сторонам треугольника A1B1C1, поэтому перпендикуляры, опущенные из
вершин треугольника ABC на стороны треугольника A2B2C2,
пересекаются в одной точке. Следовательно, в одной точке пересекаются
перпендикуляры, опущенные из вершин треугольника A2B2C2 на
стороны треугольника ABC. Остается заметить, что при повороте
на 90°, переводящем треугольник A2B2C2 в A1B1C1, эти
перпендикуляры переходят в прямые, проходящие через стороны
треугольника A1B1C1 параллельно соответствующим сторонам
треугольника ABC.
-
7.44.
-
Нужно выяснить, в каком случае выполняется равенство
AB12 + BC12 + CA12 = BA12 + CB12 + AC12.
Вычитая из обеих частей этого равенства
величину AA22 + BB22 + CC22, переходим к соотношению
A2B12 + B2C12 + C2A12 = B2A12 + C2B12 + A2C12,
т. е. (b1 – a2)2 + (c1 – b2)2 + (a1 – c2)2 = (a1 – b2)2 + (b1 – c2)2 + (c1 – a2)2, где ai,bi и ci-
координаты точек Ai,Bi и Ci на прямой l. После сокращения
получаем a2b1 + b2c1 + c2a1 = a1b2 + b1c2 + c1a2,
а значит,
(b2 – a2)(c1 – b1) = (b1 – a1)(c2 – b2),
т. е.
|
A2B2
|
: |
B2C2
|
= |
A1B1
|
: |
B1C1
|
|
.
-
7.45.
-
Можно считать, что длина стороны данного правильного
треугольника равна 2. Пусть PA = 2a, PB = 2b и PC = 2c; A1,B1
и C1- проекции центров вписанных окружностей треугольников PBC,PCA и PAB на прямые BC, CA и AB. Согласно задаче 3.2
AB12 + BC12 + CA12 = (1 + a – c)2 + (1 + b – a)2 + (1 + c – b)2 = 3 + (a – c)2 + (b – a)2 + (c – b)2 = BA12 + CB12 + AC12.
-
7.46.
-
Отрезки, на которые биссектрисы делят стороны
треугольника, легко вычисляются. В результате получаем, что если
перпендикуляры, восставленные из оснований биссектрис, пересекаются, то
|
|
ж
и
|
ac
b + c
|
ц
ш
|
2
|
+ |
ж
и
|
ab
a + c
|
ц
ш
|
2
|
+ |
ж
и
|
bc
a + b
|
ц
ш
|
2
|
= |
ж
и
|
ab
b + c
|
ц
ш
|
2
|
+ |
ж
и
|
bc
a + c
|
ц
ш
|
2
|
+ |
ж
и
|
ac
a + b
|
ц
ш
|
2
|
, |
|
т. е.
|
0 = |
a2(c – b)
b + c
|
+ |
b2(a – c)
a + c
|
+ |
c2(b – a)
a + b
|
= – |
(b – a)(a – c)(c – b)(a2 + b2 + c2)
(a + b)(a + c)(b + c)
|
. |
|
-
7.47.
-
Пусть (ai,bi)- координаты точки Ai,
(x,y)- координаты точки X. Тогда уравнение, которому
удовлетворяет точка X, перепишется в виде
| c = |
е
| ki ((x – ai)2 + (x – bi)2) = |
ж
и
|
е
| ki |
ц
ш
|
(x2 + y2) – |
ж
и
|
2 |
е
| kiai |
ц
ш
|
x – |
ж
и
|
2 |
е
| kibi |
ц
ш
|
y + |
е
| ki (ai2 + bi2)
|
.
Если коэффициент при x2 + y2 отличен от нуля, то это уравнение задает
окружность или пустое множество, а если он равен нулю, то уравнение
задает прямую, плоскость или пустое множество.
Замечание.
Если в случае а) точки A1,…,An лежат на одной прямой l, то
эту прямую можно выбрать в качестве оси Ox. Тогда bi = 0, а значит,
коэффициент при y равен нулю, т. е. центр окружности лежит на
прямой l.
-
7.48.
-
Пусть прямая l высекает на данных окружностях
дуги A1B1 и A2B2 величиной 2a1 и 2a2; O1
и O2- центры окружностей, R1 и R2- их радиусы.
Пусть K — точка пересечения касательных в точках A1 и A2. По
теореме синусов KA1 : KA2 = sin a2 : sin a1,
т. е. KA1sin a1 = KA2sin a2. А так как KO12 = KA12 + R12
и KO22 = KA22 + R22,
то (sin 2a2)KO12 – (sin 2a2)KO22 = (R1sin a1)2 – (R2sin a2)2 = q. Аналогично доказывается, что и
остальные точки пересечения касательных принадлежат геометрическому
месту таких точек X,
что (sin 2a1)XO12 – (sin 2a2)XO22 = q. Это
ГМТ- окружность, центр которой лежит на прямой O1O2 (см.
замечание к задаче 7.47).
-
7.49.
-
Пусть AM : BM : CM = p : q : r. Все
точки X, удовлетворяющие соотношению (q2 – r2)AX2 + (r2 – p2)BX2 + (p2 – q2)CX2 = 0, лежат на одной прямой (см. задачу 7.47), а точки M,N
и O удовлетворяют этому соотношению.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:48.

 Глава 7. Задачи для самостоятельного решения |
Глава 7. Задачи для самостоятельного решения | 

 Глава 7. Задачи для самостоятельного решения |
Глава 7. Задачи для самостоятельного решения | 

