| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
9.1.
-
Пусть C1- середина стороны AB.
Тогда CC1 + C1A > CA и BC1 + C1C > BC. Поэтому 2CC1 + BA > CA + BC,
т. е. mc > (a + b – c)/2.
Пусть точка Cў симметрична C относительно точки C1.
Тогда CC1 = C1Cў и BCў = CA. Поэтому 2mc = CCў < CB + BCў = CB + CA,
т. е. mc < (a + b)/2.
-
9.2.
-
Из предыдущей задачи следует ma < (b + c)/2, mb < (a + c)/2
и mc < (a + b)/2, поэтому сумма длин медиан меньше периметра.
Пусть O- точка пересечения медиан треугольника ABC.
Тогда BO + OA > BA, AO + OC > AC и CO + OB > CB. Складывая эти неравенства
и учитывая, что AO = 2ma/3, BO = 2mb/3, CO = 2mc/3,
получаем ma + mb + mc > 3(a + b + c)/4.
-
9.3.
-
Пусть M1 и M2- диаметрально противоположные
точки окружности. Тогда M1Ak + M2Ak і M1M2 = 2. Складывая эти
неравенства для k = 1,…,n, получаем (M1A1 + … + M1An) + (M2A1 + … + M2An) і 2n. Поэтому либо M1A1 + … + M1An і n, и тогда положим M = M1, либо M2A1 + … + M2An і n, и тогда
положим M = M2.
-
9.4.
-
В качестве K можно взять середину отрезка PQ. В самом
деле, тогда AiK Ј (AiP + AiQ)/2
(см. задачу 9.1), причем хотя бы
одно неравенство строгое, так как точки Ai, не могут все лежать
на прямой PQ.
-
9.5.
-
Пусть Ai и Bi- положения конца минутных стрелок
часов с номером i в моменты t и t + 30 мин, Oi-
центр i-х часов, а O- центр стола.
Тогда OOi Ј (OAi + OBi)/2 для любого i (см. задачу 9.1). Ясно,
что в некоторый момент точки Ai и Bi не лежат на прямой OiO,
т. е. по крайней мере одно из n неравенств становится строгим. Тогда
либо OO1 + … + OOn < OA1 + … + OAn,
либо OO1 + … + OOn < OB1 + … + OBn.
-
9.6.
-
Решая систему уравнений x + y = c, x + z = b, y + z = a, получаем
x = ( – a + b + c)/2, y = (a – b + c)/2, z = (a + b – c)/2. Положительность чисел x,y
и z следует из неравенства треугольника.
-
9.7.
-
По неравенству треугольника a2 > (b – c)2 = b2 – 2bc + c2,b2 > a2 – 2ac + c2 и c2 > a2 – 2ab + b2. Складывая эти неравенства,
получаем требуемое.
-
9.8.
-
Можно считать, что a і b і c. Докажем, что a = b. В
самом деле, если b < a, то b Ј la и c Ј la, где l < 1.
Поэтому bn + cn Ј 2lnan. При достаточно большом n
имеем 2ln < 1 и получаем противоречие с неравенством треугольника.
-
9.9.
-
Так как c(a – b)2 + 4abc = c(a + b)2, то a(b – c)2 + b(c – a)2 + c(a – b)2 + 4abc – a3 – b3 – c3 = a((b-c)2 – a2) + b((c – a)2 – b2) + c((a + b)2 – c2) = (a + b – c)(a – b + c)( – a + b + c).
(Последнее равенство проверяется простым вычислением.) Все три
сомножителя положительны в силу неравенства треугольника.
-
9.10.
-
Легко проверить, что abc|p – q| = |(b – c)(c – a)(a – b)|. А так
как |b – c| < a, |c – a| < b и |a – b| < c, то |(b – c)(c – a)(a – b)| < abc.
-
9.11.
-
Обозначим длины отрезков так, что a1 Ј a2 Ј a3 Ј a4 Ј a5. Если все треугольники, которые можно составить
из этих отрезков, не остроугольные, то a32 і a12 + a22,a42 і a22 + a32 и a52 і a32 + a42.
Поэтому a52 і a32 + a42 і (a12 + a22) + (a22 + a32) і 2a12 + 3a22. Так как a12 + a22 і 2a1a2, то
2a12 + 3a22 > a12 + 2a1a2 + a22 = (a1 + a2)2. Приходим к
неравенству a52 > (a1 + a2)2, противоречащему неравенству
треугольника.
-
9.12.
-
Первое решение. Введем новые
переменные x = – a + b + c, y = a – b + c, z = a + b – c. Тогда a = (y + z)/2, b = (x + z)/2,c = (x + y)/2, т. е. нужно доказать неравенство xyz Ј (x + y)(y + z)(x + z)/8
или 6xyz Ј x(y2 + z2) + y(x2 + z2) + z(x2 + y2). Последнее неравенство
следует из того, что 2xyz Ј x(y2 + z2), 2xyz Ј y(x2 + z2),2xyz Ј z(x2 + y2), так как x,y,z- положительные числа.
Второе решение. Так как 2S = absin g и sin g
= c/2R,
то abc = 4SR. По формуле Герона (a + b – c)(a – b + c)( – a + b + c) = 8S2/p.
Поэтому нужно доказать, что 8S2/p Ј 4SR, т. е. 2S Ј pR. Так
как S = pr, приходим к неравенству 2r Ј R (см. задачу 10.26).
-
9.13.
-
Введем новые переменные x = ( – a + b + c)/2,
y = (a – b + c)/2
и z = (a + b – c)/2.
Тогда числа x,y,z положительны
и a = y + z, b = x + z,c = x + y.
Несложные, но несколько громоздкие вычисления показывают,
что
| a2b(a – b + b2c(b – c) + c2a(c – a) = 2(x3z + y3x + z3y – xyz(x + y + z)) = 2xyz |
ж
и
|
|
x2
y
|
+ |
y2
z
|
+ |
z2
x
|
– x – y – z |
ц
ш
|
|
. Так
как
, то
| 2x Ј x |
ж
и
|
x
y
|
+ |
y
x
|
ц
ш
|
= |
x2
y
|
+ y
|
. Аналогично
| 2y Ј y |
ж
и
|
y
z
|
+ |
z
y
|
ц
ш
|
= |
y2
z
|
+ z
|
и
| 2z Ј z |
ж
и
|
z
x
|
+ |
x
z
|
ц
ш
|
= |
z2
x
|
+ x
|
. Складывая эти неравенства, получаем
|
x2
y
|
+ |
y2
z
|
+ |
z2
x
|
і x + y + z
|
.
-
9.14.
-
Пусть O- точка пересечения диагоналей
четырехугольника ABCD. Тогда AC + BD = (AO + OC) + (BO + OD) = (AO + OB) + (OC + OD) > AB + CD.
-
9.15.
-
Согласно предыдущей задаче AB + CD < AC + BD. Складывая
это неравенство с неравенством AB + BD Ј AC + CD, получаем 2AB < 2AC.
-
9.16.
-
Докажем сначала, что если P- периметр выпуклого
четырехугольника ABCD, a d1 и d2- длины его диагоналей,
то P > d1 + d2 > P/2. Ясно, что AC < AB + BC и AC < AD + DC, поэтому
AC < (AB + BC + CD + AD)/2 = P/2. Аналогично BD < P/2. Следовательно,
AC + BD < P. С другой стороны, складывая неравенства AB + CD < AC + BD
и BC + AD < AC + BD (см. задачу 9.14), получаем P < 2(AC + BD).
Пусть P- периметр внешнего четырехугольника, Pў- периметр
внутреннего. Тогда d > P/2, а так как Pў < P (задача 9.27, б),
то dў < Pў < P < 2d.
-
9.17.
-
Пусть ломаная наименьшей длины самоперсекающаяся.
Рассмотрим два пересекающихся звена. Вершины этих звеньев могут
соединяться одним из трех способов (рис. 9.2). Рассмотрим новую
ломаную, у которой два пересекающихся звена заменены на штриховые
звенья (см. рис. 9.2). При этом снова получается замкнутая
ломаная, но ее длина меньше, чем у исходной, так как сумма
длин противоположных сторон выпуклого четырехугольника меньше
суммы длин диагоналей. Получено противоречие, поэтому замкнутая
ломаная наименьшей длины не может иметь пересекающихся звеньев.
-
9.18.
-
Докажем, что число сторон у такого многоугольника не
больше 5. Предположим, что все диагонали многоугольника A1… An
имеют одинаковую длину и n і 6. Тогда отрезки A1A4, A1A5,A2A4 и A2A5 имеют одинаковую длину, так как они являются
диагоналями этого многоугольника. Но в выпуклом
четырехугольнике A1A2A4A5 отрезки A1A5 и A2A4 являются
противоположными сторонами, a A1A4 и A2A5- диагоналями.
Поэтому A1A5 + A2A4 < A1A4 + A2A5. Получено противоречие.
Ясно также, что правильный пятиугольник и квадрат удовлетворяют
требуемому условию.
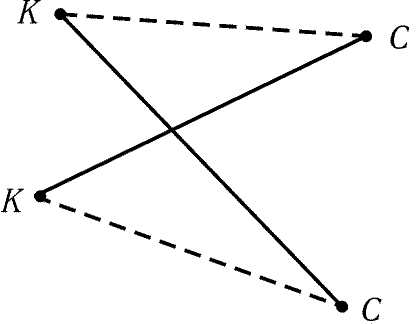
Рис. 9.3
9.19. Рассмотрим все разбиения данных точек на пары разноцветных
точек. Этих разбиений конечное число, поэтому найдется разбиение, для
которого сумма длин отрезков, заданных парами точек разбиения,
наименьшая. Покажем, что тогда эти отрезки не будут пересекаться. В
самом деле, если бы два отрезка пересекались, то мы смогли бы выбрать
разбиение с меньшей суммой длин отрезков, заменив диагонали выпуклого
четырехугольника на его противоположные стороны (рис. 9.3).
9.20. Пусть ApAp + 1 и AqAq + 1- несмежные
стороны n-угольника A1… An (т. е. |p – q| і 2).
Тогда ApAp + 1 + AqAq + 1 < ApAq + Ap + 1Aq + 1. Запишем все такие
неравенства и сложим их. Для каждой стороны найдется ровно n – 3
несмежных с ней сторон, поэтому любая сторона входит в n – 3
неравенства, т. е. в левой части полученной суммы стоит (n – 3)p, где
p- сумма длин сторон n-угольника. Диагональ AmAn входит
в два неравенства: для p = n, q = m и p = n – 1, q = m – 1, поэтому в правой
части стоит 2d, где d- сумма длин диагоналей. Итак,
(n – 3)p < 2d. Следовательно, p/n < d/(n(n – 3)/2), что и требовалось.
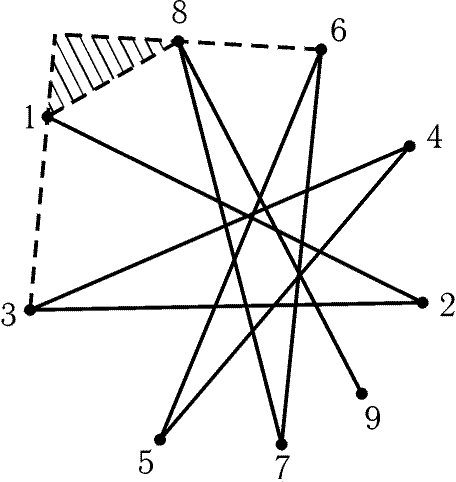
Рис. 9.4
9.21. Рассмотрим произвольную замкнутую ломаную с вершинами
в вершинах данного многоугольника. Если у нее есть два непересекающихся
звена, то, заменив эти звенья на диагонали заданного ими
четырехугольника, мы увеличим сумму длин звеньев; при этом,
однако, одна замкнутая ломаная может распасться на две. Докажем,
что в случае нечетного числа звеньев после нескольких таких
операций в конце концов получится все же замкнутая ломаная (так
как сумма длин звеньев каждый раз увеличивается, таких операций
возможно лишь конечное число). Одна из получившихся замкнутых
ломаных должна иметь нечетное число звеньев, но тогда любое
из оставшихся звеньев не пересекается хотя бы с одним из звеньев
этой ломаной (см. задачу 23.1, в), значит, в конце концов, получится
лишь одна замкнутая ломаная.
Будем теперь последовательно строить ломаную с попарно
пересекающимися звеньями (рис. 9.4). Например, вершина 10 должна
лежать внутри заштрихованного треугольника, поэтому расположение
вершин именно такое, как на рис. 9.4. Значит, выпуклому многоугольнику
A1A3A5… A2n + 1A2… A2n соответствует ломаная
A1A2A3… A2n + 1A1.
-
9.22.
-
Пусть длина третьей стороны равна n. По неравенству
треугольника 3,14 – 0,67 < n < 3,14 + 0,67. Так как n- целое число,
то n = 3.
-
9.23.
-
Ясно, что AB + BC > AC, BC + CD > BD, CD + DE > CE, DE + EA > DA,EA + AB > EB. Складывая все эти неравенства, получаем, что сумма длин
диагоналей пятиугольника меньше удвоенного периметра.
Сумма длин диагоналей больше суммы длин сторон «лучей звезды»,
а она в свою очередь больше периметра пятиугольника (рис. 9.5).
-
9.24.
-
Предположим, что c- не наименьшая сторона,
например a Ј c. Тогда a2 Ј c2 и b2 < (a + c)2 Ј 4c2.
Поэтому a2 + b2 < 5c2. Получено противоречие.
-
9.25.
-
Так как c > |b – a| и a = 2S/ha, b = 2S/hb, c = 2S/hc,
то
. Значит, в
нашем случае hc < 20 · 12/8 = 30.
-
9.26.
-
Возьмем на сторонах AB, BC, CA точки C2, A2, B2
так, что A1B2||AB, B1C2||BC, C1A2||CA (рис. 9.6). Тогда
A1 B1 < A1B2 + B2B1 = (1 – l)AB + (2l – 1)CA.
Аналогично B1C1 < (1 – l)BC + (2l – 1)AB
и C1A1 < (1 – l)CA + (2l – 1)BC. Складывая эти неравенства,
получаем P1 < lP.
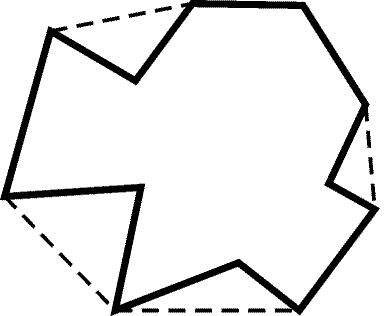
Рис. 9.7
Ясно, что A1B1 + A1C > B1C, т. е. A1B1 + (1 – l)BC > l · CA.
Аналогично B1C1 + (1 – l)CA > l · AB
и C1A1 + (1 – l)AB > l · BC. Складывая эти неравенства,
получаем P1 > (2l – 1)P.
9.27. а) При переходе от невыпуклого многоугольника к его
выпуклой оболочке некоторые ломаные, образованные сторонами,
заменяются прямолинейными отрезками (рис. 9.7). Остается заметить,
что длина ломаной больше длины отрезка с теми же концами.
б) Построим на сторонах внутреннего многоугольника полуполосы,
обращенные наружу; параллельные края полуполос перпендикулярны
соответствующей стороне многоугольника (рис. 9.8). Обозначим
через P ту часть периметра внешнего многоугольника, которая
находится внутри этих полуполос. Тогда периметр внутреннего
многоугольника не превосходит P, а внешнего больше P.
9.28. Так как AO + BO > AB, BO + OC > BC и CO + OA > AC, то AO + BO + CO > (AB + BC + CA)/2. Поскольку треугольник ABC содержит треуголь-
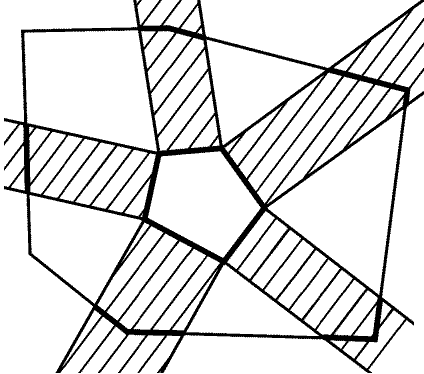
Рис. 9.8
ник ABO,
то AB + BO + OA < AB + BC + CA (см. задачу 9.27, б), т. е. BO + OA < BC + CA.
Аналогично AO + OC < AB + BC и CO + OB < CA + AB. Складывая эти неравенства,
получаем AO + BO + CO < AB + BC + CA.
9.29. Достаточно доказать, что ABCE и BCDE-
параллелограммы. Достроим треугольник ABE до
параллелограмма ABC1E. Тогда периметры треугольников BC1E и ABE
равны, поэтому равны периметры треугольников BC1E и BCE.
Следовательно, C1 = C, так как иначе один из треугольников BC1E
и BCE лежит внутри другого и их периметры не могут быть равны.
Поэтому ABCE- параллелограмм. Аналогично доказывается,
что BCDE- параллелограмм.
-
9.30.
-
Ясно, что 2 = 2S = absin g Ј ab Ј b2,
т. е. b і Ц2.
-
9.31.
-
Так как EH- средняя линия треугольника ABD,
то SAEH = SABD/4. Аналогично SCFG = SCBD/4.
Поэтому SAEH + SCFG = SABCD/4.
Аналогично SBFE + SDGH = SABCD/4. Следовательно,
SABCD = 2SEFGH = EG · HFsin a, где a- угол между
прямыми EG и HF. Так как sin a Ј 1, то SABCD Ј EG · HF.
Складывая равенства
|
®
EG
|
= |
®
EB
|
+ |
®
BC
|
+ |
®
CG
|
|
и
|
®
EG
|
= |
®
EA
|
+ |
®
AD
|
+ |
®
DG
|
|
, получаем
| 2 |
®
EG
|
= ( |
®
EB
|
+ |
®
EA
|
) + ( |
®
BC
|
+ |
®
AD
|
) + ( |
®
DG
|
+ |
®
CG
|
) = |
®
BC
|
+ |
®
AD
|
|
. Поэтому EG Ј (BC + AD)/2.
Аналогично HF Ј (AB + CD)/2. Следовательно,
|
SABCD Ј EG · HF Ј (AB + CD)(BC + AD)/4. |
|
-
9.32.
-
Согласно задаче 9.31 SABCD Ј (AB + CD)(BC + AD)/4.
Так как ab Ј (a + b)2/4, то SABCD Ј (AB + CD + AD + BC)2/16 = 1.
-
9.33.
-
Опустим из точек B и C перпендикуляры BB1
и CC1 на прямую AM. Тогда 2SAMB + 2SAMC = AM · BB1 + AM · CC1 Ј AM · BC, так как BB1 + CC1 Ј BC.
Аналогично 2SBMC + 2SBMA Ј BM · AC
и 2SCMA + 2SCMB Ј CM · AB. Складывая эти неравенства,
получаем требуемое.
-
9.34.
-
Пусть на сторонах A1A2, A2A3,…, AnA1 выбраны
точки B1,…,Bn; O- центр окружности. Пусть далее
Sk = SOBkAk + 1Bk + 1 = (OAk + 1 · BkBk + 1sin j)/2,
где j- угол между OAk + 1 и BkBk + 1. Так
как OAk + 1 = R и sin j Ј 1, то Sk Ј (R · BkBk + 1)/2.
Поэтому S = S1 + … + Sn Ј R(B1B2 + … + BnB1)/2, т. е. периметр
многоугольника B1B2… Bn не меньше 2S/R.
-
9.35.
-
Имеем 2SAOB Ј AO · OB Ј (AO2 + BO2)/2, причем
равенство возможно, только если РAOB = 90° и AO = BO.
Аналогично 2SBOC Ј (BO2 + CO2)/2, 2SCOD Ј (CO2 + DO2)/2
и 2SDOA Ј (DO2 + AO2)/2. Складывая эти неравенства, получаем
2S = 2(SAOB + SBOC + SCOD + SDOA) Ј AO2 + BO2 + CO2 + DO2,
причем равенство возможно, только если AO = BO = CO = DO
и РAOB = РBOC = РCOD = РDOA = 90°,
т. е. ABCD- квадрат и точка O- его центр.
-
9.36.
-
Нужно доказать, что SABC/SAMN і 4. Так как
AB = AM + MB = AM + AN = AN + NC = AC, то
|
|
SABC
SAMN
|
= |
AB · AC
AM · AN
|
= |
(AM + AN)2
AM · AN
|
і 4. |
|
-
9.37.
-
Воспользуемся формулой Герона: S2 = p(p – a)(p – b)(p – c).
Так как p – a = (p1 – a1) + (p2 – a2), a (x + y)2 і 4xy,
то (p – a)2 і 4(p1 – a1)(p2 – a2).
Аналогично (p – b)2 і 4(p1 – b1)(p2 – b2),(p – c)2 і 4(p1 – c1)(p2 – c2) и p2 і 4p1p2. Перемножая эти
неравенства, получаем требуемое.
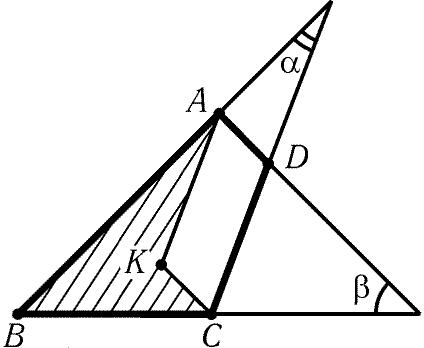
Рис. 9.9
9.38. Для определенности можно считать, что пересекаются
лучи BA и CD, BC и AD (рис. 9.9). Тогда, если достроить
треугольник ADC до параллелограмма ADCK, точка K окажется внутри
четырехугольника ABCD. Поэтому 2S і 2SABK + 2SBCK = AB · AKsin a + BC · CKsin b
= AB · CDsin a + BC · ADsin b. Равенство достигается, если точка D лежит на
отрезке AC.
Пусть точка Dў симметрична точке D относительно серединного
перпендикуляра к отрезку AC. Тогда 2S = 2SABCDў = 2SABDў + 2SBCDў Ј AB · ADў + BC · CDў = AB · CD + BC · AD.
9.39. Согласно неравенству между средним геометрическим и
средним арифметическим
|
a
a
|
+ |
b
b
|
+ |
c
g
|
і 3 | 3
Ц
|
abc/(abg)
|
= 3/2
|
, так как
и
(см. задачу 1.34).
9.40. Неравенства a < a1, b < b1 и g < g1 не
могут выполняться одновременно. Поэтому, например, a1 Ј a Ј 90°, а значит, sin a1 Ј sin a. Следовательно,
2S1 = a1b1sin a1 Ј k2absin a
= 2k2S.
9.41. а) Пусть хорды AE и BD пересекают диаметр CM в
точках K и L. Тогда AC2 = CK · CM и BC2 = CL · CM. Значит,
CK/CL = AC2/BC2 < 4. Кроме того, AE/BD = AE/AC < 2. Следовательно,
SACE/SBCD =
= AE · CK/(BD · CL) < 8.
б) Пусть H- середина отрезка BC. Так как РCBD = РBCD = РABD, то D- точка пересечения биссектрис
треугольника ABC. Поэтому AD/DH = AB/BH > 1. Следовательно,
SMAN > SABC/4 и SBCD = BC · DH/2 < BC · AH/4 = SABC/2.
9.42. Отрежем от полученного многоугольника прямоугольники
со стороной h, построенные внешним образом на сторонах исходного
многоугольника (рис. 9.10). При этом кроме исходного многоугольника
останутся еще некоторые четырехугольники, из которых можно
составить многоугольник, описанный около окружности радиуса h.
Сумма площадей этих четырехугольников больше площади окружности
радиуса h, т. е. больше ph2. Ясно также, что сумма площадей
отрезанных прямоугольников равна Ph.
9.43. Пусть s,s1,…,sn- площади квадрата и
составляющих его прямоугольников, S,S1,…,Sn- площади
описанных около них кругов. Докажем, что sk Ј 2Sk/p.
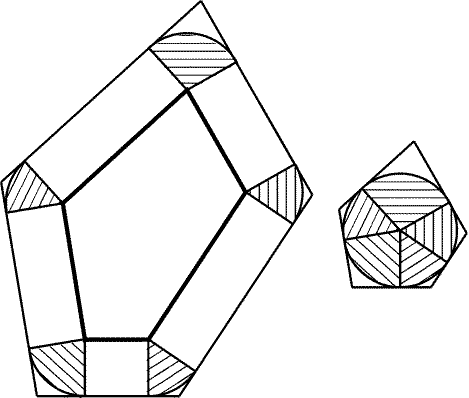
Рис. 9.10
В самом
деле, если стороны прямоугольника равны a и b, то sk = ab
и Sk = pR2, где
. Поэтому
sk = ab Ј (a2 + b2)/2 = 2pR2/p = 2Sk/p. Следовательно,
2S/p = s = s1 + … + sn Ј 2(S1 + … + Sn)/p.
9.44. Пусть для определенности ABC —
треугольник наименьшей площади. Обозначим точку пересечения
диагоналей AD и EC через F.
Тогда SABCDE <
SAED + SEDC + SABCF.
Так как точка F лежит на отрезке EC
и SEAB і
SCAB, то SEAB і SFAB.
Аналогично SDCB і
SFCB.
Поэтому SABCF = SFAB + SFCB
Ј
SEAB + SDCB.
Следовательно, SABCDE < SAED + SEDC + SEAB + SDCB;
это даже более сильное неравенство, чем требовалось.
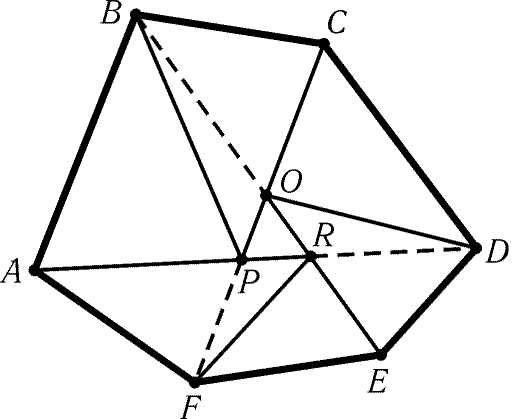
Рис. 9.11
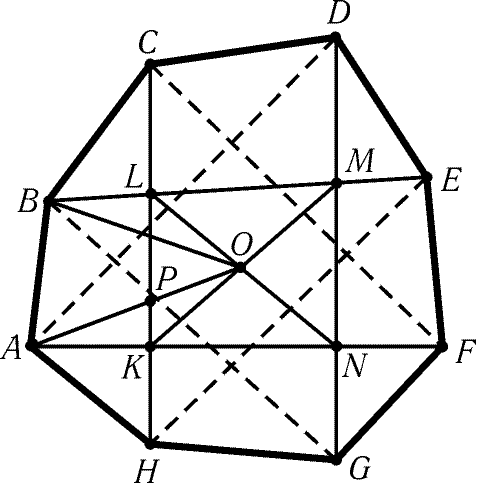
Рис. 9.12
9.45. а) Обозначим точки пересечения диагоналей AD и CF,
CF и BE, BE и AD через P,Q,R соответственно (рис. 9.11).
Четырехугольники ABCP и CDEQ не имеют общих внутренних точек, так
как стороны CP и QC лежат на прямой CF, а отрезки AB
и DE- по разные стороны от нее. Аналогично
четырехугольники ABCP, CDEQ и EFAR но имеют попарно общих
внутренних точек. Поэтому сумма их площадей не превосходит S.
Следовательно, сумма площадей треугольников ABP, BCP, CDQ, DEQ, EFR,FAR не превосходит S, т. е. площадь одного из них, например ABP,
не превосходит S/6. Точка P лежит на отрезке CF, поэтому либо
точка C, либо точка F удалена от прямой AB не больше, чем
точка P. Следовательно, либо SABC Ј SABP Ј S/6,
либо SABF Ј SABP Ј S/6.
б) Пусть ABCDEFGH- выпуклый восьмиугольник (рис. 9.12). Докажем
сначала, что четырехугольники ABEF, BCFG, CDGH и DEHA имеют
общую точку. Ясно, что пересечением ABEF и CDGH является
некоторый выпуклый четырехугольник KLMN. Отрезки AF
и HC лежат внутри углов DAH и AHE соответственно, поэтому
точка K лежит внутри четырехугольника DEHA. Аналогично доказывается,
что точка M лежит внутри четырехугольника DEHA,
т. е. весь отрезок KM лежит внутри его. Аналогично отрезок LN
лежит внутри четырехугольника BCFG. Точка пересечения диагоналей KM
и LN принадлежит всем нашим четырехугольникам; обозначим
ее O. Разобьем восьмиугольник на треугольники, соединив точку O
с вершинами. Площадь одного из этих треугольников, например ABO,
не превосходит S/8. Отрезок AO пересекает сторону KL
в некоторой точке P, поэтому SABP Ј SABO Ј S/8. Так как
точка P лежит на диагонали CH, то либо SABC Ј SABP Ј S/8, либо SABH Ј SABP Ј S/8.
-
9.46.
-
Проведем через все вершины многоугольника прямые,
параллельные одной паре сторон квадрата, и разобьем тем самым
квадрат на полоски. Каждая такая полоска отрезает от многоугольника
трапецию или треугольник. Достаточно доказать, что длина одного из
оснований этих трапеций больше 0,5. Предположим, что длины
оснований всех трапеций не превосходят 0,5. Тогда площадь каждой
трапеции не превосходит половины высоты полоски, ее заключающей.
Поэтому площадь многоугольника, равная сумме площадей трапеций
и треугольников, на которые он разрезан, не превосходит половины
суммы высот полосок, т. е. не превосходит 0,5. Получено противоречие.
-
9.47.
-
а) Пусть P1,…,Pn- данные точки. Соединим
точку P1 с вершинами квадрата. При этом получится четыре
треугольника. Затем для k = 2,…,n проделаем следующую операцию.
Если точка Pk лежит строго внутри одного из полученных ранее
треугольников, то соединим ее с вершинами этого треугольника. Если
точка Pk лежит на общей стороне двух треугольников, то соединим ее с
вершинами этих треугольников, противолежащими общей стороне. После
каждой такой операции в обоих случаях число треугольников увеличивается
на два. В результате получится 2(n + 1) треугольников. Сумма площадей
этих треугольников равна 1, поэтому площадь одного из них не
превосходит 1/(2(n + 1)).
б) Рассмотрим наименьший выпуклый многоугольник, содержащий
данные точки. Пусть он имеет k вершин. Если k = n, то
этот k-угольник можно разбить на n – 2 треугольников диагоналями,
выходящими из одной вершины. Если же k < n, то внутри k-угольника
лежит n – k точек и его можно разбить на треугольник способом,
указанным в предыдущей задаче. При этом получится k + 2(n – k – 1) = 2n – k – 2 треугольников. Так как k < n, то 2n – k – 2 > n – 2.
Сумма площадей треугольников разбиения меньше 1, а их
количество не меньше n – 2, поэтому площадь хотя бы одного из
них не превосходит 1/(n – 2).
-
9.48.
-
а) Можно считать, что описанный n-угольник
A1… An и вписанный n-угольник B1… Bn расположены
так, что прямые AiBi пересекаются в центре O данного круга.
Пусть Ci и Di- середины сторон AiAi + 1 и BiBi + 1.
Тогда SOBiCi = p · OBi · OCi,SOBiDi = p · OBi · ODi
и SOAiCi = p · OAi · OCi, где p = (sin AiOCi)/2. Так
как OAi : OCi = OBi : ODi,
то SOBiCi2 = SOBiDiSOAiCi. Остается заметить, что
площадь части круга, заключенной внутри угла AiOCi,
больше SOBiCi, а площади частей вписанного и описанного
n-угольников, заключенных внутри этого угла, равны SOBiDi
и SOAiCi.
б) Пусть радиус окружности равен R. Тогда P1 = 2nRsin (p/n),P2 = 2nRtg (p/n) и L = 2pR. Нужно доказать, что sin xtg x > x2
при 0 < x Ј p/3. Так как
|
ж
и
|
sin x
x
|
ц
ш
|
2
|
і |
ж
и
|
1 – |
x2
6
|
ц
ш
|
2
|
= 1 – |
x2
3
|
+ |
x4
36
|
|
и
| 0 < cos x Ј 1 – |
x2
2
|
+ |
x2
24
|
|
(см. приложение в
конце главы), остается проверить, что
| 1 – |
x2
3
|
+ |
x4
36
|
і 1 – |
x2
2
|
+ |
x4
24
|
|
, т. е. 12x2 > x4.
При x Ј p/3 это неравенство выполняется.
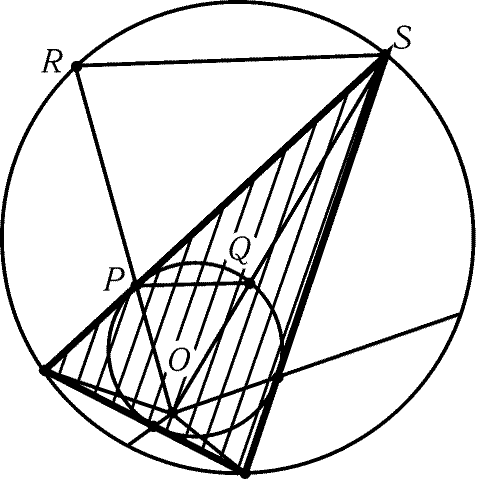
Рис. 9.13
9.49. Пусть O- центр гомотетии, переводящей вписанную
окружность в описанную. Разобьем плоскость лучами, выходящими из
точки O и проходящими через вершины многоугольника и точки
касания его сторон с вписанной окружностью (рис. 9.13). Достаточно
доказать требуемое неравенство для частей кругов и многоугольника,
заключенных внутри каждого из образованных этими лучами углов.
Пусть стороны угла пересекают вписанную и описанную окружности в
точках P,Q и R,S соответственно, причем P- точка касания,
а S- вершина многоугольника. Площади частей кругов больше
площадей треугольников OPQ и ORS, поэтому достаточно доказать, что
2SOPS Ј SOPQ + SORS. Так как 2SOPS = 2SOPQ + 2SPQS
и SORS = SOPQ + SPQS + SPRS, остается доказать,
что SPQS Ј SPRS. Это неравенство очевидно, так как высоты
треугольников PQS и PRS, опущенные на основания PQ и RS, равны,
a PQ < RS.
9.50. Достаточно доказать, что оба треугольника содержат
центр O круга. Докажем, что если треугольник ABC, помещенный в круг
радиуса 1, не содержит центра круга, то его площадь меньше 1. В самом
деле, для любой точки, лежащей вне треугольника, найдется прямая,
проходящая через две вершины и отделяющая эту точку от третьей вершины.
Пусть для определенности прямая AB разделяет точки C и O.
Тогда hc < 1 и AB < 2, поэтому S = hc · AB/2 < 1.
-
9.51.
-
а) Построим на сторонах многоугольника внутренним
образом прямоугольники со второй стороной R = S/P. Они покроют
не весь многоугольник (эти прямоугольники перекрываются и могут
вылезать за его пределы, а сумма их площадей равна площади
многоугольника). Непокрытая точка удалена ото всех сторон многоугольника
больше, чем на R, поэтому круг радиуса R с центром
в этой точке целиком лежит внутри многоугольника.
б) Из задачи а) следует, что во внутренний многоугольник
можно поместить круг радиуса S2/P2. Ясно, что этот круг лежит
внутри внешнего многоугольника. Остается доказать, что если внутри
многоугольника лежит круг радиуса R, то R Ј 2S/P. Для этого
соединим центр O круга с вершинами. Тогда многоугольник
разобьется на треугольники с площадями hiai/2, где hi-
расстояние от точки O до i-й стороны, а ai- длина i-й
стороны. Так как hi і R, то
.
-
9.52.
-
Рассмотрим сначала случай, когда две стороны
параллелограмма лежат на прямых AB и AC, а четвертая вершина X
лежит на стороне BC. Если BX : CX = x : (1 – x), то отношение
площади параллелограмма к площади треугольника равно 2x(1 – x) Ј 1/2.
В общем случае проведем параллельные прямые, содержащие
пару сторон данного параллелограмма (рис. 9.14). Площадь данного
параллелограмма не превосходит суммы площадей заштрихованных
параллелограммов, а они относятся к разобранному выше случаю.
Если прямые, содержащие пару сторон данного параллелограмма,
пересекают лишь две стороны треугольника, то можно ограничиться
одним заштрихованным параллелограммом.
-
9.53.
-
Рассмотрим сначала такой случай: две вершины A и B
треугольника ABC лежат на одной стороне PQ параллелограмма.
Тогда AB Ј PQ и высота, опущенная на сторону AB, не больше высоты
параллелограмма. Поэтому площадь треугольника ABC не больше половины
площади параллелограмма.
Если же вершины треугольника лежат на разных сторонах
параллелограмма, то две из них лежат на противоположных сторонах.
Проведем через третью вершину треугольника прямую, параллельную
этим сторонам (рис. 9.15). Она разрезает параллелограмм на два
параллелограмма, а треугольник- на два треугольника, причем
у обоих треугольников две вершины лежат на сторонах параллелограмма.
Приходим к рассмотренному случаю.
-
9.54.
-
Пусть M- середина наибольшей стороны BC
данного остроугольного треугольника ABC. Окружность радиуса MA
с центром M пересекает лучи MB и MC в точках B1 и C1.
Так как РBAC < 90°, то MB < MB1. Пусть для
определенности РAMB Ј РAMC, т. е. РAMB Ј 90°. Тогда AM2 + MB2 Ј AB2 Ј BC2 = 4MB2,
т. е. AM Ј Ц3BM. Если AH- высота треугольника ABC,
то AH · BC = 2, а значит, SAB1C1 = B1C1 · AH/2 = AM · AH Ј Ц3BM · AH = Ц3.
-
9.55.
-
а) Пусть AB- наибольшая диагональ или сторона
данного многоугольника M. Многоугольник M заключен внутри полосы,
образованной перпендикулярами к отрезку AB, проходящими через
точки A и B. Проведем к многоугольнику M две опорные прямые,
параллельные AB; пусть они пересекают многоугольник M в точках C
и D. В результате многоугольник M заключен в прямоугольник, площадь
которого равна 2SABC + 2SABD Ј 2S.
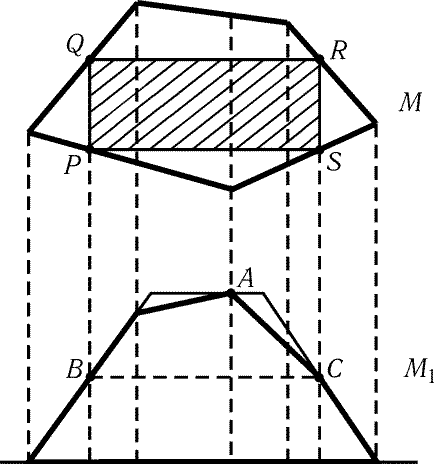
Рис. 9.16
б) Пусть M- исходный многоугольник, l- произвольная прямая.
Рассмотрим многоугольник M1, одна из сторон которого-
проекция M на l, а длины сечений многоугольников M и M1 любой
прямой, перпендикулярной l, равны (рис. 9.16). Легко проверить, что
многоугольник M1 тоже выпуклый, причем его площадь равна S.
Пусть A- наиболее удаленная от l точка многоугольника M1.
Прямая, равноудаленная от точки A и прямой l, пересекает стороны
многоугольника M1 в точках B и C. Проведем через точки B
и C опорные прямые. В результате вокруг многоугольника M1
будет описана трапеция (через точку A тоже можно провести
опорную прямую); площадь этой трапеции не менее S. Если высота
трапеции (т. е. расстояние от точки A до прямой l) равна h, то
ее площадь равна h · BC, а значит, h · BC і S. Рассмотрим
сечения PQ и RS многоугольника M прямыми, перпендикулярными l и
проходящими через B и C. Длины этих сечений равны h/2,
поэтому PQRS- параллелограмм, причем его площадь равна BC · h/2 і S/2.
-
9.56.
-
а) Заключим многоугольник в полосу, образованную
параллельными прямыми. Будем сдвигать эти прямые параллельно
до тех пор, пока на каждую из них не попадут некоторые вершины A
и B многоугольника. Затем проделаем то же самое для полосы,
образованной прямыми, параллельными AB. На эти прямые попадут
некоторые вершины C и D (рис. 9.17). Исходный многоугольник
заключен в параллелограмм, поэтому площадь этого параллелограмма
не меньше 1. С другой стороны, сумма площадей треугольников ACB
и ADB равна половине площади параллелограмма, поэтому площадь одного
из этих треугольников не меньше 1/4.
б) Как и в задаче а), заключим многоугольник в полосу,
образованную параллельными прямыми, так, чтобы вершины A
и B лежали на этих прямых (рис. 9.18). Пусть ширина этой полосы равна d.
Проведем три прямые, делящие эту полосу на равные полосы шириной d/4.
Пусть первая и третья прямые пересекают стороны многоугольника в
точках K,L и M,N соответственно.
Продолжим стороны, на которых лежат точки K,L,M и N, до
пересечения со сторонами исходной полосы и с прямой, делящей
ее пополам. При этом образуются две трапеции со средними
линиями KL и MN, высоты которых равны d/2. Так как эти
трапеции покрывают весь многоугольник, сумма их площадей не
меньше его площади, т. е. (d · KL + d · MN)/2 і 1. Сумма
площадей треугольников AMN и BKL, содержащихся в исходном
многоугольнике, равна (3d · MN + 3d · KL)/8 і 3/4. Поэтому
площадь одного из этих треугольников не меньше 3/8.
-
9.57.
-
Докажем, что найдутся даже три последовательные вершины, удовлетворяющие требуемому условию.
Пусть ai- угол между i-й и (i + 1)-й сторонами,
bi = p – ai, а ai- длина i-й стороны.
а) Площадь треугольника, образованного i-й и (i + 1)-й сторонами,
равна Si = (aiai + 1sin ai)/2. Пусть S- наименьшая из этих
площадей.
Тогда 2S Ј aiai + 1sin ai, поэтому (2S)n Ј (a12… an2)(sin a1…sin an) Ј a12… an2.
Согласно неравенству между средним арифметическим и средним
геометрическим (a1… an)1/n Ј (a1 + … + an)/n, поэтому
2S Ј (a1… an)2/n Ј (a1 + … + an)2/n2. Так как
ai Ј pi + qi, где pi и qi- проекции i-й стороны на
вертикальную и горизонтальную стороны квадрата,
то a1 + … + an Ј (p1 + … + pn) + (q1 + … + qn) Ј 4.
Поэтому 2S Ј 16n2, т. е. S Ј 8/n2.
б) Воспользуемся доказанным выше неравенством
| 2S Ј (a1…an)2/n(sin a1…sin an)1/n Ј |
16
n2
|
(sin a1…sin an)
|
. Так как sin ai = sin bi
и b1 + … + bn = 2p, то (sin a1…sin an)1/n = (sin b1…sin bn)1/n Ј (b1 + … + bn)/n = 2p/n.
Поэтому 2S Ј 32p/n3, т. е. S Ј 16p/n3.
-
9.58.
-
Пусть li- длина i-го звена ломаной, ai
и bi- длины его проекций на стороны квадрата. Тогда li Ј ai + bi. Следовательно, 1000 = l1 + … + ln Ј (a1 + … + an) + (b1 + … + bn), т. е. либо a1 + … + an і 500,
либо b1 + … + bn і 500. Если сумма длин проекций звеньев на
сторону длиной 1 не меньше 500, то на одну из точек стороны
проецируется не менее 500 различных звеньев ломаной, т. е.
перпендикуляр к стороне, проходящий через эту точку, пересекает ломаную
по крайней мере в 500 точках.
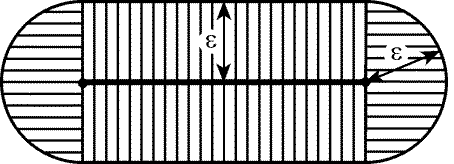
Рис. 9.19
9.59. Геометрическое место точек, удаленных от данного отрезка
не более чем на e, изображено на рис. 9.19. Площадь этой фигуры
равна pe2 + 2el,
где l- длина отрезка. Построим такие
фигуры для всех N звеньев данной ломаной. Так как соседние
фигуры имеют N – 1 общих кругов радиуса e с центрами
в неконцевых вершинах ломаной, то покрытая этими фигурами
площадь не превосходит Npe2 + 2e(l1 + … + ln) – (N – 1)pe2 = 2eL + pe2. Эти фигуры покрывают весь квадрат, так как любая
точка квадрата удалена от некоторой точки ломаной меньше чем на e.
Поэтому 1 Ј 2eL + pe2, т. е.
.
-
9.60.
-
Разобьем квадрат на n вертикальных полосок, содержащих
по n
точек каждая. Точки внутри каждой полосы соединим сверху
вниз и получим n ломаных. Эти ломаные можно соединить в одну
ломаную двумя способами (рис. 9.20, а и б ). Рассмотрим отрезки,
соединяющие разные полосы. Объединение всех таких отрезков,
полученных обоими способами, представляет собой пару ломаных,
причем сумма длин горизонтальных проекций звеньев каждой из
них не превосходит 1. Поэтому сумма длин горизонтальных проекций
соединяющих отрезков для одного из способов не превосходит 1.
Рассмотрим именно это соединение. Сумма длин горизонтальных
проекций для соединяющих звеньев не превосходит 1, а для всех
остальных звеньев не превосходит (n – 1)(h1 + … + hn), где hi
- ширина i-й полосы. Ясно, что h1 + … + hn = 1. Сумма
вертикальных проекций всех звеньев ломаной не превосходит n. В итоге
получаем, что сумма вертикальных и горизонтальных проекций всех звеньев
не превосходит 1 + (n – 1) + n = 2n, поэтому и длина ломаной не
превосходит 2n.
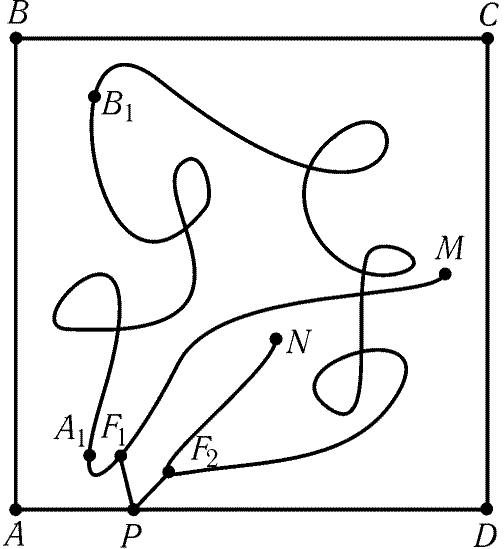
Рис. 9.21
9.61. Пусть M и N- концы ломаной. Будем идти по
ломаной из M в N. Пусть A1- первая из встретившихся нам
точек ломаной, удаленных от какой-либо вершины квадрата на
расстояние 0,5. Рассмотрим вершины квадрата, соседние с этой вершиной.
Пусть B1- первая после A1 точка ломаной, удаленная от одной
из этих вершин на расстояние 0,5. Вершины квадрата, ближайшие к
точкам A1 и B1, обозначим A и B соответственно (рис. 9.21).
Часть ломаной от M до A1 обозначим через L1, от A1
до N — через L2. Пусть X и Y- множества точек,
лежащих на AD и удаленных не более чем на 0,5 от L1 и L2
соответственно. По условию X и Y покрывают всю сторону AD. Ясно,
что A принадлежит X, а D не принадлежит X, поэтому D
принадлежит Y, т. е. оба множества X и Y не пусты. Но каждое из
них состоит из нескольких отрезков, поэтому они должны иметь общую
точку P. Следовательно, на L1 и L2 существуют точки F1
и F2, для которых PF1 Ј 0,5 и PF2 Ј 0,5.
Докажем, что F1 и F2- искомые точки. В самом деле,
F1F2 Ј F1P + PF2 Ј 1. С другой стороны, идя в F2 из F1,
мы должны пройти через точку B, а F1B1 і 99 и F2B1 і 99,
так как
точка B1 удалена от стороны BCне больше, чем на 0,5, а F1 и F2
удалены от стороны AD не больше чем на 0,5.
-
9.62.
-
Пусть РA = РB. Достаточно доказать, что
если AD < BC, то РD = РC. Возьмем на стороне BC
точку D1 так, что BD1 = AD. Тогда ABD1D- равнобедренная
трапеция. Поэтому РD > РD1DA = РDD1B > РC.
-
9.63.
-
Пусть B1 и C1 - проекции точек B и C на
основание AD. Так как РBAB1 < РCDC1 и BB1 = CC1,
то AB1 > DC1 и поэтому B1D < AC1. Следовательно,
BD2 = B1D2 + B1B2 < AC12 + CC12 = AC2.
-
9.64.
-
Пусть углы B и D четырехугольника ABCD тупые.
Тогда точки B и D лежат внутри окружности с диаметром AC. Так как
расстояние между любыми двумя точками, лежащими внутри окружности,
меньше ее диаметра, то BD < AC.
-
9.65.
-
В равнобедренной трапеции ABCD диагонали AC и BD
равны. Поэтому BM + (AM + CM) і BM + AC = BM + BD і DM.
-
9.66.
-
Пусть O - середина отрезка BD. Точка A лежит
внутри окружности с диаметром BD, поэтому OA < BD/2. Кроме того,
FO = CD/2. Следовательно, 2FA Ј 2FO + 2OA < CD + BD.
-
9.67.
-
Отложим на лучах AB, AC и AD отрезки ABў, ACў
и ADў длиной 1/AB,1/AC и 1/AD. Тогда AB : AC = ACў :
ABў, т. е. DABC ~ DACўBў. Коэффициент подобия
этих треугольников равен 1/(AB · AC), поэтому BўCў = BC/(AB · AC). Аналогично CўDў = CD/(AC · AD) и BўDў = BD/(AB · AD).
Подставив эти выражения в неравенство BўDў Ј BўCў + CўDў и домножив
обе части на AB · AC · AD, получим требуемое.
-
9.68.
-
Ясно, что SABCD = SABC + SACD = 2SAMC + 2SANC = 2(SAMN + SCMN). Если отрезок AM пересекает
диагональ BD в точке A1, то SCMN = SA1MN < SAMN. Значит,
SABCD < 4SAMN.
-
9.69.
-
Диагонали AC и BD пересекаются в точке O. Пусть
для определенности точка P лежит внутри треугольника AOB. Тогда
AP + BP Ј AO + BO < AC + BD (см. решение задачи 9.28) и CP + DP < CB + BA + AD.
-
9.70.
-
Пусть ri, Si и pi- радиусы вписанных
окружностей, площади и полупериметры полученных треугольников. Тогда
| Q і 2 |
е
| ri = 2 |
е
| (Si/pi) > 4 |
е
| (Si/P) = 4S/P
|
.
-
9.71.
-
Пусть AC Ј BD. Опустим из вершин A и C
перпендикулярны AA1 и CC1 на диагональ BD. Тогда AA1 + CC1 Ј AC Ј BD, а значит, AA1 Ј BD/2 или CC1 Ј BD/2.
-
9.72.
-
Проведем через концы отрезка KL прямые, ему
перпендикулярные, и рассмотрим проекции на них вершин четырехугольника,
а также точки пересечения с ними прямых AC и BD (рис. 9.22). Пусть
для определенности точка A лежит внутри полосы, заданной этими
прямыми, а точка B- вне ее. Тогда можно считать, что D лежит
внутри полосы, так как иначе BD > KL, и доказательство завершено. Так
как
|
|
AAў
BBў
|
Ј |
A1K
B1K
|
= |
C1L
D1L
|
Ј |
CCў
DDў
|
, |
|
то либо AAў Ј CCў (и тогда AC > KL), либо BBў і DDў (и
тогда BD > KL).
-
9.73.
-
Введем такие обозначения, как на рис. 9.23. Все
рассматриваемые параллелограммы имеют общий центр (задача 1.7). Длины
сторон параллелограмма P3 равны a + a1 и b + b1, а длины сторон
параллелограмма P1 равны a + a1 + 2x и b + b1 + 2y, поэтому нужно
проверить, что a + a1 + 2x Ј 2(a + a1) или b + b1 + 2y Ј 2(b + b1),
т. е. 2x Ј a + a1 или 2y Ј b + b1. Предположим, что a + a1 < 2x
и b + b1 < 2y. Тогда
и
. С другой стороны, равенство площадей заштрихованных
параллелограммов (см. задачу 4.19) показывает, что ab = xy = a1b1, а
значит,
. Получено противоречие.
-
9.74.
-
Пусть углы пятиугольника равны a, a + g, a + 2g,a + 3g, a + 4g, где a,g і 0. Так как сумма углов
пятиугольника равна 3p, то 5a + 10g
= 3p. Из выпуклости
пятиугольника следует, что все его углы меньше p,
т. е. a + 4g < p, или – 5a/2 – 10g > – 5p/2. Складывая последнее
неравенство с равенством 5a + 10g
= 3p, получаем 5a/2 > p/2,
т. е. a > p/5 = 36°.
-
9.75.
-
Ясно, что
| 4 = AE2 = | |
®
AB
|
+ |
®
BC
|
+ |
®
CD
|
+ |
®
DE
|
|2 = | |
®
AB
|
+ |
®
BC
|
|2 + 2( |
®
AB
|
+ |
®
BC
|
, |
®
CD
|
+ |
®
DE
|
) + | |
®
CD
|
+ |
®
DE
|
|2
|
. Так как РACE = 90°, то
| ( |
®
AB
|
+ |
®
BC
|
, |
®
CD
|
+ |
®
DE
|
) = ( |
®
AC
|
, |
®
CE
|
) = 0
|
.
Поэтому
| 4 = | |
®
AB
|
+ |
®
BC
|
|2 + | |
®
CD
|
+ |
®
DE
|
|2 = AB2 + BC2 + CD2 + DE2 + 2( |
®
AB
|
, |
®
BC
|
) + 2( |
®
CD
|
, |
®
DE
|
)
|
, т. е. достаточно
доказать, что
и
. Поскольку
| 2( |
®
AB
|
, |
®
BC
|
) = 2abcos (180° – РABC) = 2abcos AEC = ab · CE
|
и c < CE,
то
. Второе неравенство доказывается
аналогично, так как можно ввести новые обозначения A1 = E, B1 = D,C1 = C, a1 = d, b1 = c, c1 = b, и неравенство
перепишется в виде
| a1b1c1 < 2( |
®
A1B1
|
, |
®
B1C1
|
)
|
.
-
9.76.
-
Пусть B- середина стороны A1A2 данного
шестиугольника A1… A6, O- его центр. Можно считать, что
точка P лежит внутри треугольника A1OB. Тогда PA3 і 1, так
как расстояние от точки A3 до прямой BO равно 1; PA4 і 1
и PA5 і 1, так как расстояния от точек A4 и A5 до
прямой A3A6 равны 1.
-
9.77.
-
Предположим, что радиусы описанных окружностей
треугольников ACE и BDF больше 1. Пусть O- центр описанной
окружности треугольника ACE. Тогда РABC > РAOC,РCDE > РCOE и РEFA > РEOA, а значит, РB + РD + РF > 2p. Аналогично РA + РC + РE > 2p,
т. е. сумма углов шестиугольника ABCDEF больше 4p. Получено
противоречие.
Замечание.
Аналогично можно доказать, что радиус описанной окружности одного из
треугольников ACE и BDF не меньше 1.
-
9.78.
-
Можно считать, что AE Ј AC Ј CE. Согласно
задаче 9.67 AD · CE Ј AE · CD + AC · DE < AE + AC Ј 2CE,
т. е. AD < 2.
-
9.79.
-
Так как РA1 = 180° – ИA2A7/2,РA3 = 180° – ИA4A2/2
и РA5 = 180° – ИA6A4/2, то
РA1 + РA3 + РA5 = 2 · 180° + (360° – ИA2A7 – ИA4A2 – ИA6A4)/2 = 2 · 180° + ИA7A6/2. Поскольку центр окружности лежит
внутри семиугольника, то ИA7A6 < 180°, поэтому
РA1 + РA3 + РA5 < 360° + 90° = 450°.
-
9.80.
-
а) Нужно доказать, что если c- гипотенуза
прямоугольного треугольника, а a и b- его катеты,
то c і (a + b)/Ц2, т. е. (a + b)2 Ј 2(a2 + b2). Ясно, что
(a + b)2 = (a2 + b2) + 2ab Ј (a2 + b2) + (a2 + b2) = 2(a2 + b2).
б) Пусть di- длина i-ой стороны многоугольника, а xi
и yi- длины ее проекций на координатные оси.
Тогда x1 + … + xn і 2a, y1 + … + yn і 2b. Согласно задаче а)
di і (xi + yi)/Ц2. Поэтому d1 + … + dn і (x1 + … + xn + y1 + … + yn)/Ц2 і Ц2(a + b).
-
9.81.
-
Возьмем отрезок длиной P и расположим на нем стороны
многоугольника следующим образом: на одном конце отрезка поместим
наибольшую сторону, на другом — следующую за ней по величине, а все
остальные стороны поместим между ними. Так как любая сторона
многоугольника меньше P/2, середина O отрезка не может находиться на
этих двух наибольших сторонах. Длина стороны, на которой находится
точка O, не превосходит P/3 (иначе первые две стороны тоже были бы
больше P/3 и сумма трех сторон была бы больше P), поэтому одна
из ее вершин удалена от O не более чем на P/6. Эта вершина
разбивает отрезок на два искомых отрезка, так как разность их длин не
превосходит 2 · P/6 = P/3.
-
9.82.
-
Пусть bk = РOAkAk + 1. Тогда xksin bk = dk = xk + 1sin (ak + 1 – bk + 1). Поэтому
| 2 |
е
| dk = |
е
| xk(sin (ak – bk) + sin bk) = 2 |
е
| xksin (ak/2)cos (ak/2 – bk) Ј 2 |
е
| xksin (ak/2)
|
.
Ясно также, что AkAk + 1 = xkcos bk + xk + 1cos (ak + 1 – bk + 1). Поэтому
| 2p = |
е
| AkAk + 1 = |
е
| xk(cos (ak – bk) + cos bk) = 2 |
е
| xkcos (ak/2)cos (ak/2 – bk) Ј 2 |
е
| xkcos (ak/2)
|
.
В обоих случаях равенство достигается, только если ak = 2bk,
т. е. O- центр вписанной окружности.
-
9.83.
-
Предположим, что центр O многоугольника M2 лежит
вне многоугольника M1. Тогда существует такая сторона AB
многоугольника M1, что многоугольник M1 и точка O лежат по
разные стороны от прямой AB. Пусть CD- сторона
многоугольника M1, параллельная AB. Расстояние между прямыми AB
и CD равно радиусу вписанной окружности S многоугольника M2,
поэтому прямая CD лежит вне окружности S. С другой стороны,
отрезок CD лежит внутри многоугольника M2. Следовательно, длина
отрезка CD меньше половины длины стороны многоугольника M2 (см.
задачу 10.66). Получено противоречие.
-
9.84.
-
Пусть A1- ближайшая к O вершина многоугольника.
Разобьем многоугольник на треугольники диагоналями, проходящими через
вершину A1. Точка O окажется в одном из этих треугольников,
например в треугольнике A1AkAk + 1. Если точка O попадет на
сторону A1Ak, то РA1OAk = p, и задача решена. Поэтому
будем считать, что точка O лежит строго внутри
треугольника A1AkAk + 1. Так как A1O Ј AkO и A1O Ј Ak + 1O, то РA1AkO Ј AkA1O и РA1Ak + 1O Ј РAk + 1A1O. Следовательно
| РAkOA1 + РAk + 1OA1 = (p – РOA1Ak – РOAkA1) + (p – РOA1Ak + 1 – РOAk + 1A1) і 2p – 2РOA1Ak-2РOA1Ak + 1 = 2p – 2РAkA1Ak + 1 = 2p – |
2p
n
|
|
, т. е. один из
углов AkOA1 и Ak + 1OA1 не меньше
.
-
9.85.
-
Пусть d- длина наибольшей диагонали (или стороны)
AB данного n-угольника. Тогда его периметр P не
превосходит pd (задача 13.42). Пусть Aiў- проекция
вершины Ai на отрезок AB. Тогда
или
(задача 9.87); пусть для определенности выполняется
первое неравенство. Тогда
|
е
| AAi > |
е
| AAiў і nd/2 > nd і P
|
, так
как n/2 і 3,5 > p. Любая точка n-угольника, достаточно близкая
к вершине A, обладает требуемым свойством.
-
9.86.
-
а) Предположим сначала, что РAi > РBi, а
для всех остальных рассматриваемых пар углов имеет место равенство.
Расположим многоугольники так, чтобы вершины A1,…,Ai совпали
с B1,…,Bi. В треугольниках A1AiAn и A1AiBn
стороны AiAn и AiBn равны и РA1AiAn > РA1AiBn, поэтому A1An > A1Bn.
Если же не равны несколько углов, то многоугольники A1… An
и B1… Bn можно включить в цепочку многоугольников,
последовательные члены которой такие, как в разобранном выше случае.
б) При полном обходе многоугольника знак минус меняется на знак плюс
столько же раз, сколько происходит обратная смена знака. Поэтому число
пар соседних вершин с разными знаками четно. Остается проверить, что
число изменений знака не может быть равно двум (число изменений знака
не равно нулю, так как сумма углов обоих многоугольников одна и та же).
Предположим, что число изменений знака равно двум. Пусть P и Q,
Pў и Qў - середины сторон многоугольников A1… An
и B1… Bn, на которых происходит смена знака. К парам
многоугольников M1 и M1ў, M2 и M2ў (рис. 9.24) можно
применить утверждение задачи а); в одном случае получим PQ > PўQў, а в
другом PQ < PўQў, чего не может быть.
-
9.87.
-
Пусть A и B- концы отрезка;
X1,…,Xn- данные точки. Так как AXi + BXi = 1, то
. Следовательно,
или
.
-
9.88.
-
Будем тянуть провод по отрезку AB, огибая при этом
встречающиеся деревья по кратчайшей дуге (рис. 9.25). Достаточно
доказать, что путь по дуге окружности не более чем в 1,6 раза длиннее
пути по прямой. Отношение длины дуги угловой величины 2j к хорде,
ее стягивающей, равно j/sin j. Так как 0 < j Ј p/2,
то j/sin j Ј p/2 < 1,6.
-
9.89.
-
Пусть деревья высотой a1 > a2 > … > an растут в
точках A1,…,An. Тогда по условию A1A2 Ј |a1 – a2| = a1 – a2,…, An – 1An Ј an – 1 – an. Следовательно, длина
ломаной A1A2… An не превосходит (a1 – a2) + (a2 – a3) + … + (an – 1 – an) = a1 – an < 100 м. Эту ломаную можно огородить
забором, длина которого не превосходит 200 м (рис. 9.26).
-
9.90.
-
Выделим в полученном многоугольнике части, по которым
произошла склейка (на рис. 9.27 эти части заштрихованы). Все стороны, не
принадлежащие заштрихованным многоугольникам, входят в периметр
исходного и полученного многоугольников. Что же касается заштрихованных
многоугольников, то их стороны, лежащие на прямой сгиба, входят в
периметр полученного многоугольника, а все остальные стороны — в периметр
исходного многоугольника. Так как у любого многоугольника сумма его
сторон, лежащих на некоторой прямой, меньше суммы остальных сторон, то
периметр исходного многоугольника всегда больше, чем периметр
полученного.
-
9.91.
-
Возьмем на ломаной две точки A и B, делящие ее
периметр пополам. Тогда AB Ј 1/2. Докажем, что все точки ломаной
лежат внутри круга радиуса 1/4 с центром в середине O отрезка AB.
Пусть M- произвольная точка ломаной, а точка M1 симметрична ей
относительно точки O. Тогда MO = M1M/2 Ј (M1A + AM)/2 = (BM + AM)/2 Ј 1/4, так как BM + AM не превосходит половины длины ломаной.
-
9.92.
-
Пусть остроугольный треугольник ABC расположен внутри
окружности S. Построим описанную окружность S1 треугольника ABC.
Так как треугольник ABC остроугольный, то угловая величина дуги
окружности S1, лежащей внутри S, больше 180°. Поэтому на
этой дуге можно выбрать диаметрально противоположные точки, т. е.
внутри окружности S содержится диаметр окружности S1.
Следовательно, радиус окружности S не меньше радиуса
окружности S1.
Аналогичное утверждение для тупоугольного треугольника не верно.
Тупоугольный треугольник лежит внутри окружности, построенной на
наибольшей стороне a как на диаметре. Радиус этой окружности
равен a/2, а радиус описанной окружности треугольника
равен a/(2sin a). Ясно, что a/2 < a/(2sin a).
-
9.93.
-
Первое решение. Любой треугольник
периметра P можно поместить в круг радиуса P/4, а если
остроугольный треугольник помещен в круг радиуса R1, то R1 і R
(задача 9.92). Поэтому P/4 = R1 і R.
Второе решение. Если 0 < x < p/2, то sin x > 2x/p.
Поэтому a + b + c = 2R(sin a + sin b + sin g) > 2R(2a + 2b + 2g)/p = 4R.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:48.

 Глава 9. Приложение. Некоторые неравенства |
Глава 9. Приложение. Некоторые неравенства | 

 Глава 9. Приложение. Некоторые неравенства |
Глава 9. Приложение. Некоторые неравенства | 





