VIII Заочный конкурс учителей математики.

I. Решите задачи.

N1. В шахматном фестивале участвовали англичане, немцы и французы. Каждый англичанин сыграл ровно с пятью немцами и двумя французами, каждый немец – с шестью англичанами и четырьмя французами, а каждый француз – с тремя англичанами и с одинаковым числом немцев. Найдите это число.

N2. В треугольнике АВС Н и М – точки пересечения высот и медиан соответственно. Найдите угол ВАС, если биссектриса этого угла перпендикулярна прямой МН.

N3. Докажите, что если x > 0, y > 0 и z > 0, то .

N4. Дан пространственный шарнирный четырехугольник АВСD (длины его сторон и их порядок – зафиксирован, а углы могут меняться). Докажите, что существует такое его положение, при котором в тетраэдре АВСD двугранные углы при ребрах AC и BD – прямые.

N5. Найдите все целые значения q, для которых уравнение х² + px + p = q имеет целый корень только при одном целом значении р.

II. Методический блок.

В предложенных текстах (N6 – N8) могут содержаться математические ошибки (как в "ответах", так и в "решениях"). Укажите все ошибки и, если "решение" не верно, то приведите верное решение.

N6. "Задача". Решите уравнение: arctgx + arctg(–2) = arcctg(–2).

"Ответ": 0,75.

"Решение". Так как arctgx = arctg2 + arcctg(–2), то x = tg(arctgx) = tg(arctg2 + arcctg(–2)) =

N7. "Задача". Рассматриваются "слова" длины 100, составленные только из букв A, B и C. Каких "слов" больше: тех, в которых каждый из фрагментов AB и AC встречается четное число раз, или тех, в которых каждый из таких фрагментов встречается нечетное число раз?

"Ответ": поровну.

"Решение". Рассмотрим "слово", в котором оба фрагмента встречаются нечетное число раз. Заменим в нем первый из фрагментов на другой (AB на AC, или наоборот). Получим слово, у которого оба фрагмента встречаются четное число раз. Это соответствие является взаимно-однозначным, поэтому "слов" обоих видов одинаковое количество.

N8. "Задача". В треугольнике ABC с углом B, равным 120°, проведены биссектрисы AA₁, BB₁ и CC₁. Найдите площадь треугольника А₁В₁С₁, если длины двух его сторон равны 4 и 5.

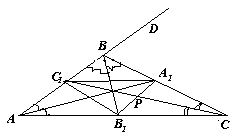
"Ответ": 10 или 6.

"Решение". На продолжении стороны AВ (за точку В) отметим точку D, тогда ∠DBC = 60°, то есть луч BC – биссектриса угла DBB₁ (см. рис.). Так как AA₁ – биссектриса угла ВАС, то А₁ – центр окружности, касающейся BB₁, BD и B₁C. Такая окружность является вневписанной для треугольника АВВ₁, поэтому, B₁A₁ – биссектриса угла ВВ₁С. Аналогично, С₁ – центр вневписанной окружности для треугольника CВВ₁, поэтому B₁C₁ – биссектриса угла ВВ₁A. Следовательно, ∠А₁В₁С₁ = 90°.

Таким образом, треугольник А₁В₁С₁ – прямоугольный, значит, его площадь S = 0,5·B₁A₁·В₁С₁ Далее возможны два случая:

1) Заданные длины сторон – это длины катетов этого треугольника, тогда его площадь S = 0,5·5·4 = 10.

2) Гипотенуза этого треугольника равна 5, а один из катетов равен 4. Тогда другой катет равен 3, то есть S = 0,5·3·4 = 6.

III. Аналитический блок.

N9. Многие планиметрические теоремы имеют аналоги в стереометрии.

1) Приведите несколько примеров:

а) планиметрических теорем и аналогичных им теорем стереометрии.

б) верных планиметрических утверждений и их неверных стереометрических аналогов

в) верных стереометрических утверждений и их неверных планиметрических аналогов.

2) Объясните, каким образом такой материал можно использовать в преподавании курса геометрии.