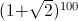 раскрыли скобки и сгрупировали слагаемые с корнем и без, получилось
раскрыли скобки и сгрупировали слагаемые с корнем и без, получилось 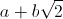 , где a и b — целые числа. Какое из чисел больше — a или b?
, где a и b — целые числа. Какое из чисел больше — a или b?Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 19 октября выслать полные решения задач (не только ответы!) обычным письмом (не заказным) по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника.
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.)
На сайте http://www.mccme.ru/ имеется также информация о математических кружках, олимпиадах и пр. Информацию о кружках можно получить также по телефону (499) 241-05-00.
Желаем успеха!
1. Было два положительных числа. Меньшее из них увеличили на 1 процент, большее — на 4 процента. При этом их сумма увеличилась на 3 процента. На сколько процентов увеличилась разница между числами?
2. В классе из 20 человек знают английский 10 человек, а немецкий 15 человек. Сколько человек в классе знают ровно один из этих двух языков? Укажите все возможные варианты.
3. На доске были написаны 4 числа. Их сложили всевозможными способами по два и получили 6 различных сумм, которые записали в возрастающем порядке: 5, 7, 8, 11, …, … (два последних числа стёрлись). (а) Какие числа стояли на месте многоточий? (б) Какие числа были изначально написаны на доске? Укажите все возможные варианты.
4. Из чисел от 1 до 1000 сначала вычеркнули делящиеся на 7, потом на 11, потом на 13. Сколько чисел было вычеркнуто на третьем шаге? Сколько осталось невычеркнутыми?
5. Обсуждая рост школьников, Вася сказал: один из восьмиклассников выше любого семиклассника. Петя сказал: любой семиклассник ниже хотя бы одного из восьмиклассников. Сказали они одно и то же (хотя разными словами) или разное?
6. Можно ли написать числа 1, 2, 3, 4, 5, …, 16 (каждое по одному разу) в таком порядке, чтобы сумма любых четырёх подряд идущих чисел делилась бы на 3?
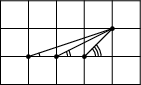
7. На клетчатой бумаге отмечены три угла (см. рисунок). Докажите, что больший из них равен сумме двух меньших.
8. В последовательности 0, 1, 00, 01, 10, 11, 000, 001, 010, 011, 100, … записаны все комбинации нулей и единиц в порядке возрастания длины (внутри одной длины в порядке возрастания): на первом месте стоит 0, на втором 1, на третьем 01 и т.д. Какая последовательность нулей и единиц стоит на тысячном месте?
9. Может ли квадрат целого числа начинаться на 20132013? Если может — приведите пример, если нет — объясните, почему.
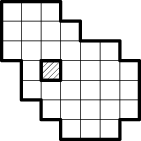
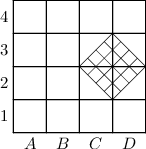
10. Квадратная карта участка местности разбита на клетки. Поверх неё положена другая карта точно того же участка местности, но меньшего масштаба и повёрнутая на 45° по часовой стрелке (см. рисунок). Карты прокололи иголкой, и оказалось, что точка прокола на обеих картах попала в одну и ту же точку местности. В какую клетку попал прокол?
11. Имеется прямоугольная коробка (параллелепипед, если говорить научно). Всегда ли противоположные углы коробки будут максимально удалёнными друг от друга точками на коробке, если считать расстояние по поверхности (сколько ползти мухе), или не всегда?
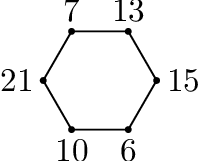
12. По кругу лежат шесть кучек камней с 7, 13, 15, 6, 10, 21 камнями. За один шаг разрешается перенести один камень из кучки в соседнюю. Какое минимальное число шагов нужно сделать, чтобы уравнять количества камней в кучках? Как это сделать? (Укажите, сколько камней надо переместить вдоль каждой стороны.) Сколько есть различных оптимальных способов?
13. В выражении 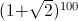 раскрыли скобки и сгрупировали слагаемые с корнем и без, получилось
раскрыли скобки и сгрупировали слагаемые с корнем и без, получилось 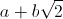 , где a и b — целые числа. Какое из чисел больше — a или b?
, где a и b — целые числа. Какое из чисел больше — a или b?
14. (Продолжение) Найдите отношение a/b с точностью до двух знаков после запятой.
15. Запишем все пятизначные числа, у которых цифры различны и идут в убывающем порядке. Каких среди них больше — чётных или нечётных?
16. Угол между часовой и минутными стрелками равен α. Прошёл час, и угол между стрелками вновь равен α. Чему равно α? Укажите все возможности. (Часы ходят точно.)
17. Можно ли замостить (без наложений и пробелов) доминошками 1×2 квадрат 5×5? (Если можно, покажите, как; если нет, докажите, что невозможно.)
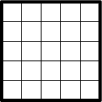
18. (Продолжение) Тот же вопрос для квадрата 5×5 с вырезанной центральной клеткой.
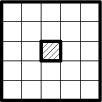
19. (Продолжение) Тот же вопрос для квадрата 5×5, из которого вырезали клетку, соседнюю с центральной.

20. (Продолжение) Тот же вопрос для фигуры с дыркой на рисунке.